23.2.1 《解直角三角形 》课件PPT沪科版数学九上

这是一份23.2.1 《解直角三角形 》课件PPT沪科版数学九上，共21页。

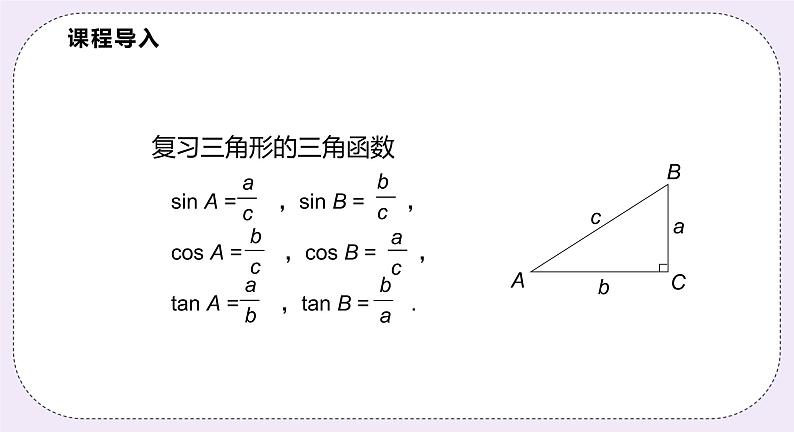
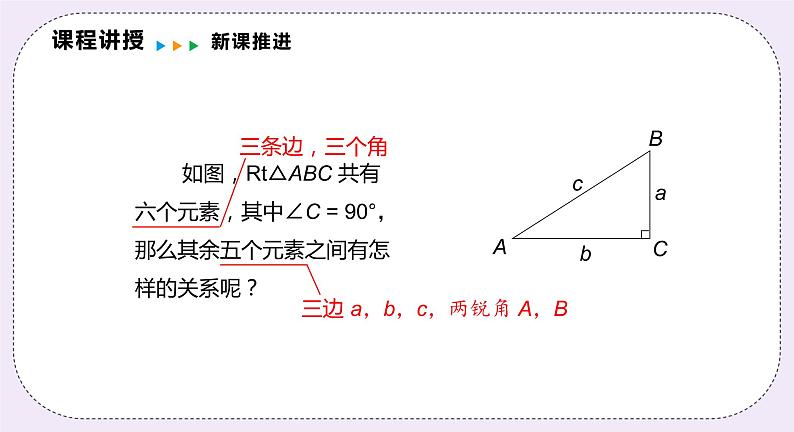
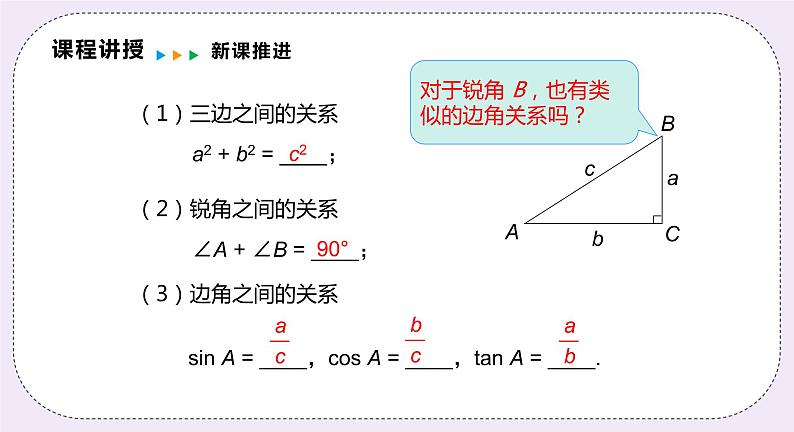
第23章解直角三角形九年级数学沪科版·上册23.2.1 解直角三角形前 言1.掌握解直角三角形的概念；（重点）2.掌握解直角三角形的依据并能熟练解题. (重点、难点)学习目标及重难点ABCD课程导入复习三角形的三角函数 如图，Rt△ABC 共有六个元素，其中∠C = 90°，那么其余五个元素之间有怎样的关系呢？三条边，三个角三边 a，b，c，两锐角 A，B课程讲授新课推进课程讲授新课推进（1）三边之间的关系a2 + b2 = ____；（2）锐角之间的关系∠A + ∠B = ____；（3）边角之间的关系sin A = ____，cos A = ____，tan A = ____.c290°对于锐角 B，也有类似的边角关系吗？ 有了以上关系，如果知道了五个元素中的两个元素（至少有一个元素是边），就可以求出其余的三个元素. 在直角三角形中，除直角外，由已知元素求出未知元素的过程，叫做解直角三角形.课程讲授新课推进课程讲授新课推进例1 在 Rt△ABC 中，∠C = 90°，∠B = 42°6′，c = 287.4，解这个直角三角形（精确到 0.1）.b = c sin B= 287.4×0.670 4 ≈ 192.7.∠A = 90°– 42°6′ = 47°54′. 课程讲授新课推进根据下列条件，解直角三角形.在 Rt△ABC 中，∠C = 90°，a = 30，∠B = 80°.课程讲授新课推进随堂小练习课程讲授新课推进例2 在Rt△ ABC 中，∠A = 55°，b = 20 cm，c = 30 cm，求三角形的面积 S△ABC（精确到 0.1 cm2）. 课程讲授新课推进 在四边形 ABCD 中，AB∥CD，AB = 4，CD = 8，AD = 6，∠D = 43°，求四边形的面积（精确到0.01）.解: 如图，作 CD 上的高 AE，43°∴AE = AD · sin 43°= 6 sin 43°课程讲授新课推进随堂小练习课程讲授新课推进43°小结课程讲授 直角三角形中除了直角外，还有两个锐角和三条边，一共5个量.已知其中两个，求剩下三个量的过程，叫做解直角三角形.课堂练习习题1 B习题2 如图，在△ABC 中，∠A = 60°，AB = 6，AC = 5 ，求 S△ABC . 课堂练习习题3 课堂练习习题4 如图，在Rt△ABC中，∠C＝90°，AC=6， ∠BAC的平分线 ，解这个直角三角形.6课堂练习如图，在Rt△ABC 中，∠C=90°，cosA = ， BC = 5， 试求AB的长.ACB习题5 课堂练习课程总结小结解法:只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素课程总结小结（3）边角之间的关系在解直角三角形的过程中，一般要用到下面一些关系：