初中数学沪科版（2024）九年级上册22.2 相似三角形的判定精品ppt课件

这是一份初中数学沪科版（2024）九年级上册22.2 相似三角形的判定精品ppt课件，共19页。PPT课件主要包含了全等三角形，观察与思考，那这样变化一下呢，探究新知，相似三角形定义，对应角，对应边，相似三角形，全等是一种特殊的相似，SSS边边边等内容，欢迎下载使用。

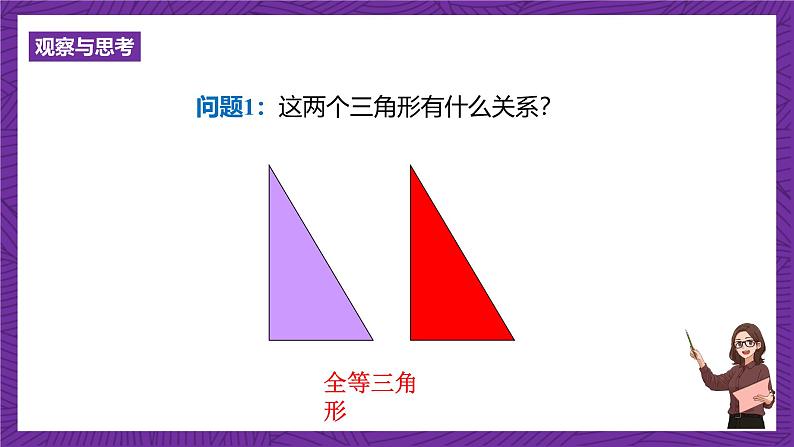
问题1：这两个三角形有什么关系？
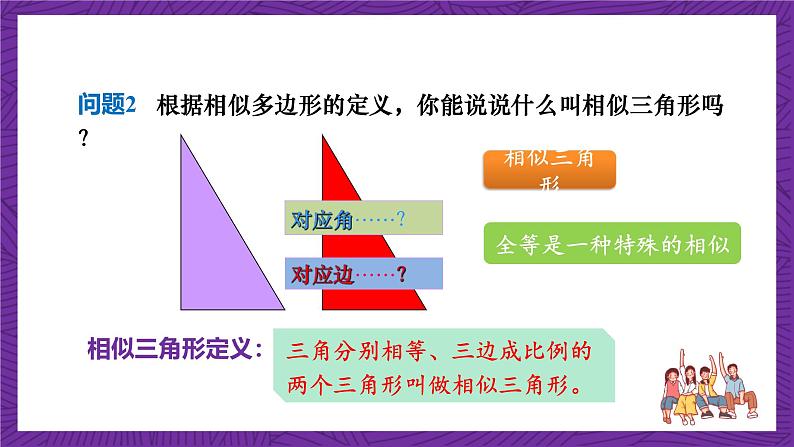
问题2 根据相似多边形的定义，你能说说什么叫相似三角形吗？
三角分别相等、三边成比例的两个三角形叫做相似三角形。
如何判定两个三角形相似？
问题3 三角形全等的性质和判定方法有哪些？
需证明对应角相等，对应边成比例．
相似三角形的判定定理1是什么？如何推导？
相似三角形判定定理1的证明
如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似．(简称：两角分别相等的两个三角形相似)．
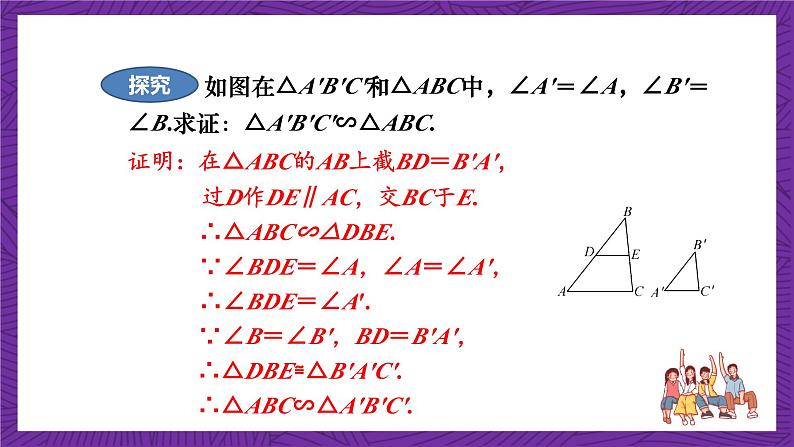
如图在△A′B′C′和△ABC中，∠A′＝∠A，∠B′＝∠B.求证：△A′B′C′∽△ABC.
证明：在△ABC的AB上截BD＝B′A′，
过D作DE∥AC，交BC于E.
∴△ABC∽△DBE.
∵∠BDE＝∠A，∠A＝∠A′，
∵∠B＝∠B′，BD＝B′A′，
∴△DBE≌△B′A′C′.
∴△ABC∽△A′B′C′.
如图，D, E分别是△ABC的边AB, AC上的点，DE∥BC, AB=7，AD=5，DE=10，求BC的长.
∴∠ADE=∠B，∠AED=∠C.
∴△ADE∽△ABC (两角分别相等的两个三角形相似).
相似三角形判定定理1的应用
已知：如图，AB⊥BD，ED⊥BD，垂足分别为点B、点D，C在线段BD上，AC⊥CE.求证：AB·DE＝BC·CD.
【分析】欲证AB·DE＝BC·CD，可证 ＝ ，则证明△ABC∽△CDE即可，由题意可知∠1＋∠2＝90°，∠1＋∠A＝90°，则∠2＝∠A.于是Rt△ABC∽Rt△CDE.
证明：∵AB⊥BD，ED⊥BD，AC⊥CE，　
∴∠B＝∠D＝90°，又∠1＋∠A＝90°，∠1＋∠2＝90°，
∴△ABC∽△CDE，
如图所示，在四边形ABCD中，AC平分∠DAB，∠ACD＝∠ABC，求证：AC2＝AB·AD.
证明：∵AC平分∠DAB，
又∵∠ACD＝∠ABC，
∴∠DAC＝∠CAB，
∴△ADC∽△ACB，
∴AC2＝AB·AD.
2．如图，等边三角形ABC的边长为3，P为BC上一点，且BP＝1，D为AC上一点，当∠APD＝60°时，CD的长为__________．
3.如图：点G在平行四边形ABCD的边DC的延长线上，AG交BC、BD于点E、F，则△AGD∽_________∽________．
4.如图，△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC.
证明: ∵ DE∥BC，EF∥AB，
∠A＝∠FEC.
∴ △ADE∽△EFC.
5．如图，已知∠1＝∠2＝∠3， 求证：△ABC∽△ADE.
∴∠1＋∠DAC＝∠3＋∠DAC，即∠BAC＝∠DAE.
∵∠2＝∠3，∠AFE＝∠DFC，
∴180°－∠2－∠DFC＝180°－∠3－∠AFE，
∴△ABC∽△ADE.
证明：∵ 在△ ABC中，∠A=40 ° ，∠B=80 ° ，
6. 如图，△ABC 和 △DEF 中，∠A=40°，∠B=80°，∠E=80 °，∠F=60 ° ．求证：△ABC ∽△DEF.
∴ ∠C=180 °－∠A－∠B=60 °.
∵ 在△DEF中，∠E=80 °，∠F=60 °.
∴ ∠B=∠E，∠C=∠F.
∴ △ABC ∽△DEF.
证明： ∵ △ABC 的高AD、BE交于点F，
∴ ∠FEA=∠FDB=90°，∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB，
利用两角判定三角形相似
定理：两角分别相等的两个三角形相似
相似三角形的判定定理1的运用