人教版九年级数学上册尖子生同步培优题典专题24.10正多边形与圆特训(原卷版+解析)

这是一份人教版九年级数学上册尖子生同步培优题典专题24.10正多边形与圆特训(原卷版+解析)，共27页。

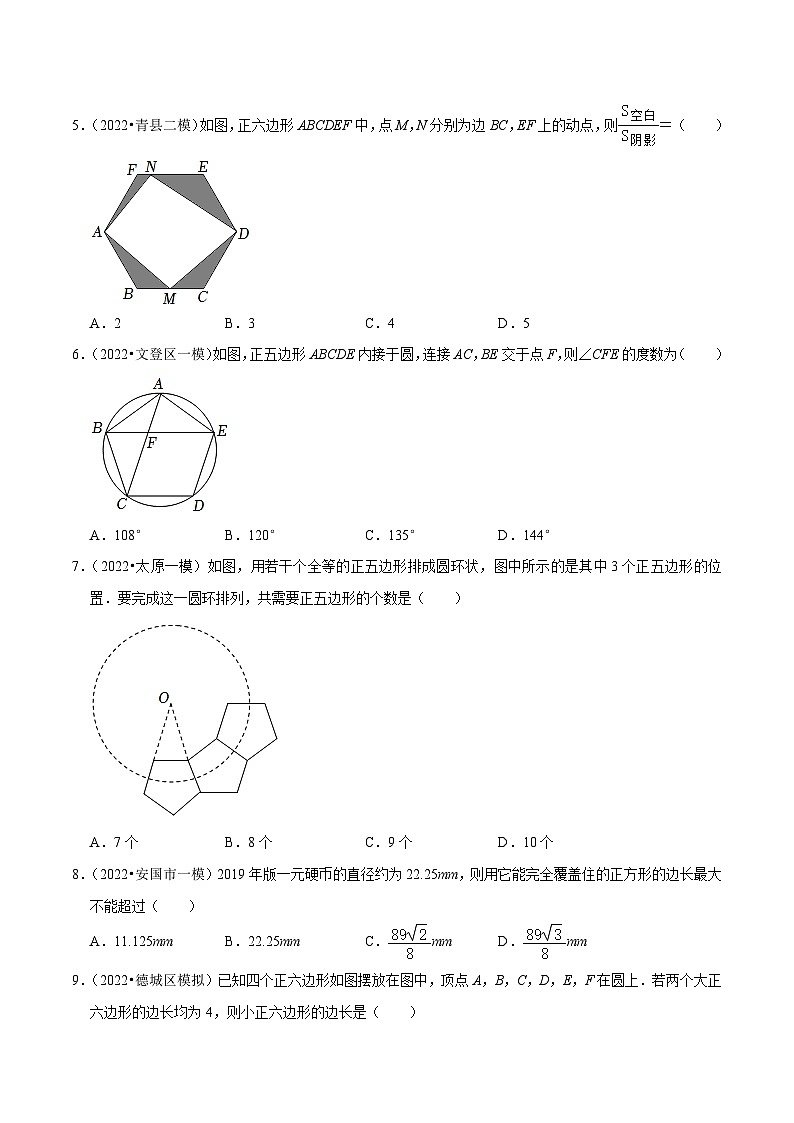
【讲练课堂】2022-2023学年九年级数学上册尖子生同步培优题典【人教版】专题24.10正多边形与圆【名师点睛】正多边形和圆（1）正多边形与圆的关系 把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．（2）正多边形的有关概念 ①中心：正多边形的外接圆的圆心叫做正多边形的中心． ②正多边形的半径：外接圆的半径叫做正多边形的半径． ③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角． ④边心距：中心到正多边形的一边的距离叫做正多边形的边心距．【典例剖析】【例1】（2020秋•六盘水期末）下列图形的周长均为16．（1）求图②菱形的面积；（结果保留根号）（2）求所有图形中最大的面积与最小的面积之差．（π取3.14，取1.73，结果精确到0.1）【例2】（2021秋•永城市月考）如图，六边形ABCDEF是⊙O的内接正六边形．（1）求证：在六边形ABCDEF中，过顶点A的三条对角线四等分∠BAF．（2）设⊙O的面积为S1，六边形ABCDEF的面积为S2，求的值（结果保留π）．【满分训练】一．选择题（共10小题）1．（2022春•新昌县期末）如图，在同一平面内，将边长相等的正六边形、正方形的一边重合，则∠1的度数为（　　）A．18° B．25° C．30° D．45°2．（2022•雅安）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为（　　）A．3 B． C． D．33．（2022•石家庄三模）如图，边长相等的正八边形和正方形部分重叠摆放在一起，已知正方形面积是2，那么非阴影部分面积是（　　）A．6 B． C． D．84．（2022•游仙区校级二模）如图，在正六边形ABCDEF中，M，N分别为边CD，BC的中点，AN与BM相交于点P，则∠APM的度数是（　　）A．110° B．120° C．118° D．122°5．（2022•青县二模）如图，正六边形ABCDEF中，点M，N分别为边BC，EF上的动点，则＝（　　）A．2 B．3 C．4 D．56．（2022•文登区一模）如图，正五边形ABCDE内接于圆，连接AC，BE交于点F，则∠CFE的度数为（　　）A．108° B．120° C．135° D．144°7．（2022•太原一模）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是（　　）A．7个 B．8个 C．9个 D．10个8．（2022•安国市一模）2019年版一元硬币的直径约为22.25mm，则用它能完全覆盖住的正方形的边长最大不能超过（　　）A．11.125mm B．22.25mm C．mm D．mm9．（2022•德城区模拟）已知四个正六边形如图摆放在图中，顶点A，B，C，D，E，F在圆上．若两个大正六边形的边长均为4，则小正六边形的边长是（　　）A． B． C． D．10．（2022•邯郸模拟）如图，在正六边形ABCDEF中，点G是AE的中点，若AB＝4，则CG的长为（　　）A．5 B．6 C．7 D．8二．填空题（共8小题）11．（2022春•二道区期末）如图是一个正多边形的玻璃碎片，这个正多边形的边数为 　 　．12．（2022春•巴中期末）如图，将边长相等的正八边形与正五边形的一边重合，并让正五边形位于正八边形内部，则∠1＝　 　．13．（2022•长春）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为 　 　厘米．14．（2022•营口）如图，在正六边形ABCDEF中，连接AC，CF，则∠ACF＝　 　度．15．（2022•陈仓区二模）如图，以正五边形ABCDE的对角线BE为边，作正方形BEFG，使点A落在正方形BEFG内，则∠ABG的度数为 　 　．16．（2022•贵阳模拟）如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，M是劣弧FG的中点．若FM＝2，则⊙O的半径为 　 　．17．（2022•绥化三模）如图，正八边形ABCDEFGH内接于⊙O，P是弧GH上的任意一点，连接CP，PE，则∠CPE的度数为 　 　．18．（2022•金山区二模）如图，如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边，BC一定是圆O的内接正n边形的一条边，那么n＝　 　．三．解答题（共6小题）19．（2021秋•日喀则市月考）如图，正方形ABCD是半径为R的⊙O内接四边形，R＝6．求正方形ABCD的边长和边心距．20．（2022•安徽二模）如图，正方形ABCD内接于⊙O，E是的中点，连接AE，DE，CE．（1）求证：AE＝DE；（2）若CE＝1，求四边形AECD的面积．21．（2021秋•昌邑区校级期末）已知，如图，正六边形ABCDEF的边长为6cm，求这个正六边形的外接圆半径R、边心距r6、面积S6．22．（2021秋•黄冈月考）如图，正五边形ABCDE，连接对角线AC，BD，设AC与BD相交于O．（1）求证：AO＝CD；（2）判断四边形AODE的形状，并说明理由．【讲练课堂】2022-2023学年九年级数学上册尖子生同步培优题典【人教版】专题24.10正多边形与圆【名师点睛】正多边形和圆（1）正多边形与圆的关系 把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．（2）正多边形的有关概念 ①中心：正多边形的外接圆的圆心叫做正多边形的中心． ②正多边形的半径：外接圆的半径叫做正多边形的半径． ③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角． ④边心距：中心到正多边形的一边的距离叫做正多边形的边心距．【典例剖析】【例1】．（2020秋•六盘水期末）下列图形的周长均为16．（1）求图②菱形的面积；（结果保留根号）（2）求所有图形中最大的面积与最小的面积之差．（π取3.14，取1.73，结果精确到0.1）【分析】（1）求出菱形的对角线的长，可得结论；（2）分别求出等边三角形，菱形，正方形，正六边形，圆的面积，可得结论．【解答】解：（1）如图，连接AC，BD交于点O．∵四边形ABCD是菱形，∴AC⊥BD，由题意AB＝4，OB＝OD＝2，∴OA＝OC＝＝＝2，∴AC＝4，∴S菱形ABCD＝•BD•AC＝××4＝8．（2）等边三角形的面积＝×（）2≈12.30，菱形的面积＝8≈13.84．正方形的面积＝16．正六边形的面积＝6××（）2＝18.45．圆的面积＝π•（）2≈20.38，所有图形中最大的面积与最小的面积之差＝20.38﹣12.30≈8.1【例2】（2021秋•永城市月考）如图，六边形ABCDEF是⊙O的内接正六边形．（1）求证：在六边形ABCDEF中，过顶点A的三条对角线四等分∠BAF．（2）设⊙O的面积为S1，六边形ABCDEF的面积为S2，求的值（结果保留π）．【分析】（1）如图，连接AE，AD，AC，根据正六边形的性质得到EF＝ED＝CD＝BC，求得＝＝＝，于是得到∠FAE＝∠EAD＝∠DAC＝∠CAB，即可得到结论；（2）如图，过O作OG⊥DE于G，连接OE，设⊙O的半径为r，推出△ODE是等边三角形，得到DE＝OD＝r，∠OED＝60°，根据勾股定理得到OG＝＝r，根据三角形和圆的面积公式即可得到结论．【解答】（1）证明：如图，连接AE，AD，AC，∵六边形ABCDEF是⊙O的内接正六边形，∴EF＝ED＝CD＝BC，∴＝＝＝，∴∠FAE＝∠EAD＝∠DAC＝∠CAB，∴过顶点A的三条对角线四等分∠BAF；（2）解：如图，过O作OG⊥DE于G，连接OE，设⊙O的半径为r，∵∠DOE＝＝60°，OD＝OE＝r，∴△ODE是等边三角形，∴DE＝OD＝r，∠OED＝60°，∴∠EOG＝30°，∴EG＝r，∴OG＝＝r，∴正六边形ABCDEF的面积＝6××r×r＝r2，∵⊙O的面积＝πr2，∴＝＝．【满分训练】一．选择题（共10小题）1．（2022春•新昌县期末）如图，在同一平面内，将边长相等的正六边形、正方形的一边重合，则∠1的度数为（　　）A．18° B．25° C．30° D．45°【分析】根据多边形内角和公式求出正三角形、正六边形每个内角的度数，再求出答案即可．【解答】解：∵正方形的每个内角的度数是90°，正六边形的每个内角的度数是＝120°，∴∠1＝120°﹣90°＝30°，故选C．2．（2022•雅安）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为（　　）A．3 B． C． D．3【分析】连接OC，OD，由正六边形ABCDEF可求出∠COD＝60°，进而可求出∠COG＝30°，根据30°角的锐角三角函数值即可求出边心距OG的长．【解答】解：连接OC，OD，∵正六边形ABCDEF是圆的内接多边形，∴∠COD＝60°，∵OC＝OD，OG⊥CD，∴∠COG＝30°，∵⊙O的周长等于6π，∴OC＝3，∴OG＝3cos30°＝，故选：C．3．（2022•石家庄三模）如图，边长相等的正八边形和正方形部分重叠摆放在一起，已知正方形面积是2，那么非阴影部分面积是（　　）A．6 B． C． D．8【分析】先将正八边形可以延长每一边构成一个大正方形，然后用大正方形的面积减去四个等腰直角三角形的面积；在用正八边形的面积减去小正方形的面积即可．【解答】解：∵正方形面积是2，∴其边长为：，如图，将正八边形的每一条边延长可得正方形ABCD，∵正八边形的每个内角为180°﹣＝135°，∴∠AEF＝45°，∴△AEF为等腰直角三角形，在Rt△AEF中，AE＝EF•sin45°＝×＝1，∴AB＝+1×2＝+2．∴正八边形的面积为：S正方形ABCD﹣4S△AEF＝＝，∴非阴影部分面积是S正八边形﹣S正方形＝﹣2＝2+．故选：C．4．（2022•游仙区校级二模）如图，在正六边形ABCDEF中，M，N分别为边CD，BC的中点，AN与BM相交于点P，则∠APM的度数是（　　）A．110° B．120° C．118° D．122°【分析】根据正六边形的性质可得AB＝BC＝CD，BN＝CM，利用全等三角形的判定与性质可得∠BNP＝∠CMB，然后利用三角形的内角和定理可得答案．【解答】解：∵六边形ABCDEF是正六边形，∴∠ABC＝∠BCD＝＝120°，AB＝BC＝CD，∵M，N分别为边CD，BC的中点，∴BN＝CM，∴△ABN≌△BCM（SAS），∴∠BNP＝∠CMB，∵∠CBM＝∠PBN，∴∠BPN＝∠BCD＝120°，∴∠APM＝120°，故选：B．5．（2022•青县二模）如图，正六边形ABCDEF中，点M，N分别为边BC，EF上的动点，则＝（　　）A．2 B．3 C．4 D．5【分析】连接AD，作FP⊥AD于点P，EQ⊥AD于点Q，由正六边形的性质可得∠EAP＝60°，设各边长为a，则AF＝a，然后利用勾股定理及面积公式可得答案．【解答】解：连接AD，作FP⊥AD于点P，EQ⊥AD于点Q，∵正六边形各内角为120°，∴∠EAP＝60°， 设各边长为a，则AF＝a，∴AP＝QD＝a，∴AD＝2a，FP＝＝＝a，∴S四边形AMDN＝AD•FP＝2a×a＝a2，S正六边形＝a2，∴S阴影＝S正六边形﹣S四边形AMDN＝a2﹣＝a2，∴＝＝2，故选：A．6．（2022•文登区一模）如图，正五边形ABCDE内接于圆，连接AC，BE交于点F，则∠CFE的度数为（　　）A．108° B．120° C．135° D．144°【分析】根据五边形的内角公式求出∠ABC，再由等腰三角形的性质、三角形的内角和定理可得答案．【解答】解：∵五边形ABCDE是正五边形，∴∠ABC＝×（5﹣2）×180°＝108°，∵BA＝BC，∴∠BAC＝∠BCA＝36°，同理∠ABF＝36°，∴∠CFE＝∠AFB＝180°﹣∠ABF﹣∠BAF＝180°﹣36°﹣36°＝108°，故选：A．7．（2022•太原一模）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是（　　）A．7个 B．8个 C．9个 D．10个【分析】先求出多边形的每一个内角为108°，可得到∠O＝36°，即可求解．【解答】解：∵多边形是正五边形，∴正五边形的每一个内角为：＝108°，∴∠O＝180°﹣（180°﹣108°）×2＝36°，∴正五边形的个数是360°÷36°＝10．故选：D．8．（2022•安国市一模）2019年版一元硬币的直径约为22.25mm，则用它能完全覆盖住的正方形的边长最大不能超过（　　）A．11.125mm B．22.25mm C．mm D．mm【分析】根据正方形性质得到△AOD为等腰直角三角形，根据正方形和圆的关系得到AC的长度，根据等腰直角三角形的性质求出AD的长度．【解答】解：如图所示，∵AC＝BD＝22.25mm，∴AO＝OD＝＝mm．∵四边形ABCD为正方形，∴AC⊥BD，∴△AOD为等腰直角三角形，∴AD＝AO＝mm．故选：C．9．（2022•德城区模拟）已知四个正六边形如图摆放在图中，顶点A，B，C，D，E，F在圆上．若两个大正六边形的边长均为4，则小正六边形的边长是（　　）A． B． C． D．【分析】在边长为4的大正六边形中，根据正六边形和圆的性质可求出ON和半径OD，进而得出小正六边形对应点的距离MF，再根据正六边形的性质求出半径GF，即边长FH即可．【解答】解：连接AD交PM于O，则点O是圆心，过点O作ON⊥DE于N，连接MF，取MF的中点G，连接GH，GQ，由对称性可知，OM＝OP＝EN＝DN＝2，由正六边形的性质可得ON＝4，∴OD＝＝2＝OF，∴MF＝2﹣2，由正六边形的性质可知，△GFH、△GHQ、△GQM都是正三角形，∴FH＝MF＝﹣1，故选：B．10．（2022•邯郸模拟）如图，在正六边形ABCDEF中，点G是AE的中点，若AB＝4，则CG的长为（　　）A．5 B．6 C．7 D．8【分析】如图，连接AC，EC．证明△ABC是等边三角形，利用等边三角形的性质求解．【解答】解：如图，连接AC，EC．∵ABCDEF是正六边形，∴△ACE是等边三角形，∵AB＝4，∴AC＝CE＝AE＝4，∵AG＝GE＝2，∴CG⊥AE，∴CG＝＝＝6，故选：B．二．填空题（共8小题）11．（2022春•二道区期末）如图是一个正多边形的玻璃碎片，这个正多边形的边数为 　5　．【分析】补全面图形，可得结论．【解答】解：如图，这个多边形是正五边形．故答案为：5．12．（2022春•巴中期末）如图，将边长相等的正八边形与正五边形的一边重合，并让正五边形位于正八边形内部，则∠1＝　76.5°　．【分析】利用正多边形的性质求出∠ABC，∠DBC，再求出∠ABD，可以利用等腰三角形的性质求解．【解答】解：如图，由题意，∠ABC＝＝135°，∠DBC＝＝108°，∴∠ABD＝∠ABC﹣∠DBC＝27°，∵BA＝BD，∴∠1＝∠BAD＝（180°﹣27°）＝76.5°，故答案为：76.5°．13．（2022•长春）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为 　54　厘米．【分析】根据对称性和周长公式进行解答即可．【解答】解：由图象的对称性可得，AM＝MN＝BN＝AB＝9（厘米），∴正六边形的周长为9×6＝54（厘米），故答案为：54．14．（2022•营口）如图，在正六边形ABCDEF中，连接AC，CF，则∠ACF＝　30　度．【分析】设正六边形的边长为1，正六边形的每个内角为120°，在△ABC中，根据等腰三角形两底角相等得到∠BAC＝30°，从而∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，过点B作BM⊥AC于点M，根据含30°的直角三角形的性质求出BM，根据勾股定理求出AM，进而得到AC的长，根据tan∠ACF＝＝＝即可得出∠ACF＝30°．【解答】解：设正六边形的边长为1，正六边形的每个内角＝（6﹣2）×180°÷6＝120°，∵AB＝BC，∠B＝120°，∴∠BAC＝∠BCA＝×（180°﹣120°）＝30°，∵∠BAF＝120°，∴∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，如图，过点B作BM⊥AC于点M，则AM＝CM（等腰三角形三线合一），∵∠BMA＝90°，∠BAM＝30°，∴BM＝AB＝，∴AM＝＝＝，∴AC＝2AM＝，∵tan∠ACF＝＝＝，∴∠ACF＝30°，故答案为：30．15．（2022•陈仓区二模）如图，以正五边形ABCDE的对角线BE为边，作正方形BEFG，使点A落在正方形BEFG内，则∠ABG的度数为 　54°　．【分析】根据正五边形的性质可求出角A的度数，再根据等腰三角形以及三角形的内角和可求出∠ABE，再根据正方形的性质求出∠ABG即可．【解答】解：∵正五边形ABCDE，∴∠BAE＝＝108°，AB＝BC＝CD＝DE＝AE，∴∠ABE＝∠AEB＝36°，又∵四边形BEFG是正方形，∴∠EBG＝90°，∴∠ABG＝90°﹣36°＝54°，故答案为：54°．16．（2022•贵阳模拟）如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，M是劣弧FG的中点．若FM＝2，则⊙O的半径为 　2　．【分析】根据正六边形的性质以及圆周角定理可得出四边形OFMG是菱形，进而得到半径．【解答】解：如图，连接OM，∵六边形OABCDE是正六边形，∴∠AOE＝＝120°，∵M是劣弧FG的中点．∴∠AOM＝∠EOM＝∠AOB＝60°，又∵OF＝OG＝OM，∴四边形OEMG是菱形，∴OE＝MF＝2，即⊙O的半径为2，故答案为：2．17．（2022•绥化三模）如图，正八边形ABCDEFGH内接于⊙O，P是弧GH上的任意一点，连接CP，PE，则∠CPE的度数为 　45°　．【分析】连接OD、OC、OE，根据正多边形和圆的知识求出正八边形的中心角的度数，根据圆周角定理求出∠CPE的度数．【解答】解：连接OD、OC、OE，如图所示：∵八边形ABCDEFGH是正八边形，∴∠COD＝∠DOE＝＝45°，∴∠COE＝45°+45°＝90°，∴∠CPE＝∠COE＝45°．故答案为：45°．18．（2022•金山区二模）如图，如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边，BC一定是圆O的内接正n边形的一条边，那么n＝　12　．【分析】连接OA、OB、OC，如图，利用正多边形与圆，分别计算⊙O的内接正四边形与内接正三角形的中心角得到∠AOB＝90°，∠AOC＝120°，则∠BOC＝30°，即可得到n的值．【解答】解：连接OA、OB、OC，如图，∵AB，AC分别为⊙O的内接正四边形与内接正三角形的一边，∴∠AOB＝＝90°，∠AOC＝＝120°，∴∠BOC＝∠AOC﹣∠AOB＝30°，∴n＝＝12，即BC恰好是同圆内接一个正十二边形的一边．故答案为：12．三．解答题（共4小题）19．（2021秋•日喀则市月考）如图，正方形ABCD是半径为R的⊙O内接四边形，R＝6．求正方形ABCD的边长和边心距．【分析】过点O作OE⊥BC，垂足为E．解直角三角形求出BC，OE即可．【解答】解：过点O作OE⊥BC，垂足为E．∵四边形ABCD为⊙O的内接正方形，∴∠BOC＝＝90°，∠OBC＝45°，OB＝6，∴BE＝OE．在Rt△OBE中，∠BEO＝90°，由勾股定理可得OE＝BE＝，∴BC＝2BE＝．即半径为6的圆内接正方形ABCD的边长为，边心距为．20．（2022•安徽二模）如图，正方形ABCD内接于⊙O，E是的中点，连接AE，DE，CE．（1）求证：AE＝DE；（2）若CE＝1，求四边形AECD的面积．【分析】（1）欲证明AE＝DE，只要证明＝．（2）连接BD，过点D作DF⊥DE交EC的延长线于F．证明△ADE≌△CDF（AAS），推出AE＝CF，推出S△ADE＝S△CDF，推出S四边形AECD＝S△DEF，再利用等腰三角形的性质构建方程求出DE，即可解决问题．【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝CD，∴＝，∵E是的中点，∴＝，∴+＝+，即＝，∴AE＝DE．（2）解：连接BD，AO，过点D作DF⊥DE交EC的延长线于F．∵四边形ABCD是正方形，∴∠DBC＝∠DEC＝45°，DA＝DC，∵∠EDF＝90°，∴∠F＝∠EDF﹣∠DEF＝90°﹣45°＝45°，∴DE＝DF，∵∠AED＝∠AOD＝45°，∴∠AED＝∠F＝45°，∵∠ADC＝∠EDF＝90°，∴∠ADE+∠EDC＝∠CDF+∠EDC＝90°，∴∠ADE＝∠CDF在△ADE和△CDF中，，∴△ADE≌△CDF（AAS），∴AE＝CF，∴S△ADE＝S△CDF，∴S四边形AECD＝S△DEF，∵EF＝DE＝EC+DE，EC＝1，∴1+DE＝DE，∴DE＝+1，∴S四边形AECD＝S△DEF＝DE2＝+．21．（2021秋•昌邑区校级期末）已知，如图，正六边形ABCDEF的边长为6cm，求这个正六边形的外接圆半径R、边心距r6、面积S6．【分析】连接OA，OB，过点O作OG⊥AB于G，易得△AOB是等边三角形，继而可得正六边形的外接圆半径R，然后由勾股定理求得边心距，又由S正六边形＝6S△ABO求得答案．【解答】解：连接OA，OB，过点O作OG⊥AB于G，∵∠AOB＝60°，OA＝OB，∴△AOB是等边三角形，∴OA＝OB＝6cm，即R＝6cm，∵OA＝OB＝6，OG⊥AB，∴AG＝AB＝×6＝3cm，∴在Rt△AOG中，r6＝OG＝＝3cm，∴S6＝×6×6×3＝54cm2．22．（2021秋•黄冈月考）如图，正五边形ABCDE，连接对角线AC，BD，设AC与BD相交于O．（1）求证：AO＝CD；（2）判断四边形AODE的形状，并说明理由．【分析】（1））根据正五边形的性质可知AB＝BC＝CD＝DE＝AE，∠ABC＝∠BAE＝108°，AE∥BD，所以∠ABO＝72°，∠BAO＝（180°﹣108°）＝36°，因此∠AOB＝180°﹣72°﹣36°＝72°＝∠ABO，推出AB＝AO，则CD＝AO；（2）根据圆周角定理求出∠BDE、∠E的度数，进而证明DF∥AE；证明AF∥DE，AE＝DE，即可解决问题．【解答】解：（1）∵五边形ABCDE是正五边形，∴AB＝BC＝CD＝DE＝AE，∠ABC＝∠BAE＝108°，AE∥BD，∴∠ABO＝72°，∠BAO＝（180°﹣108°）＝36°，∴∠AOB＝180°﹣72°﹣36°＝72°＝∠ABO，∴AB＝AO，∴CD＝AO；（2）四边形AODE是菱形；理由如下：∵正五边形ABCDE内接于⊙O，∴∠BDE＝＝72°，∠E＝×360°＝108°，∴∠BDE+∠E＝180°，DO∥AE；同理可证：AO∥DE，而AE＝DE，∴四边形AODE是菱形．