





- 第05讲 一元二次方程、不等式(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第06讲 函数的概念及其表示(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第08讲 函数的奇偶性、周期性(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第09讲 函数的对称性(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
- 第10讲 二次函数与幂函数(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版) 课件 0 次下载
第07讲 函数的单调性与最值(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版)
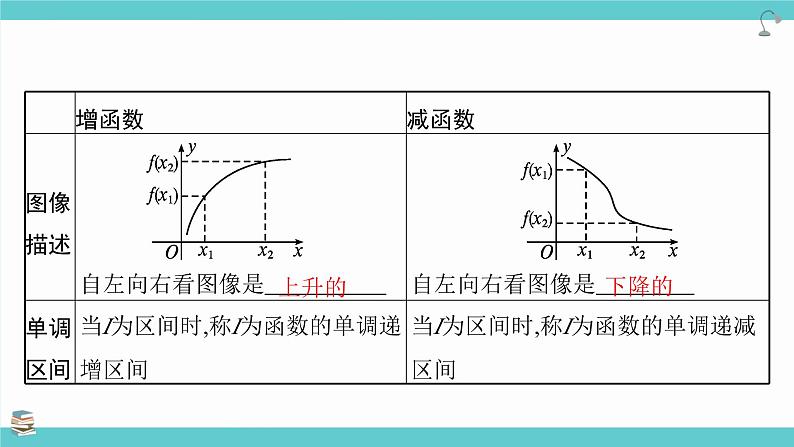
展开1.函数的单调性函数单调性及单调区间的定义
f(x1)
(1)y=f(x)在I上是增函数的充要条件是 在I上恒成立; (2)y=f(x)在I上是减函数的充要条件是 在I上恒成立. 一般地,当x1≠x2时,称 为函数y=f(x)在区间[x1,x2](x1
函数单调性的常用结论:
易错点1 忽略含参函数的分类讨论而致错
易错点2 忽略分段函数的分界点而致错
命题点1 确定函数的单调性(单调区间)
例1 (1)[2023北京高考]下列函数中,在区间(0,+∞)上单调递增的是( C )
(2)[全国卷Ⅱ]函数 f ( x )=ln( x 2-2 x -8)的单调递增区间是( D )
[解析] 由 x 2-2 x -8>0,得 x <-2或 x >4.因此,函数 f ( x )=ln( x 2-2 x -8)的定 义域是(-∞,-2)∪(4,+∞).(先求函数 f ( x )的定义域)易知函数 y = x 2-2 x -8在(-∞,-2)上单调递减,在(4,+∞)上单调递增,函数 y =ln t 为(0,+∞)上的增函数,由复合函数的单调性知, f ( x )=ln( x 2-2 x -8)的 单调递增区间是(4,+∞).故选D.
命题点2 函数单调性的应用
对已知函数解析式比较函数值大小的问题,应先将自变量转化到同一个单调区间内,再利用函数的单调性解决;对没有给出函数解析式的比较大小问题,需要先构造函数,再求函数的单调区间,最后利用函数的单调性比较大小.
例2[2024吉林长春东北师大附中校考改编]函数 f ( x )的定义域为(0,+∞),对于∀ x , y ∈(0,+∞), f ( xy )= f ( x )+ f ( y ),且当 x >1时, f ( x )<0.则 a = f ( sin 3), b = f(ln 3), c = f (21.5)的大小关系是( A )
例3[全国卷Ⅰ]函数 f ( x )在(-∞,+∞)上单调递减,且为奇函数.若 f (1)=-1,则 满足-1≤ f ( x -2)≤1的 x 的取值范围是( D )
[解析] ∵函数 f ( x )为奇函数,且 f (1)=-1,∴ f (-1)=- f (1)=1,由-1≤ f ( x - 2)≤1,得 f (1)≤ f ( x -2)≤ f (-1),(将常数转化为函数值)又函数 f ( x )在(-∞,+∞)上单调递减,∴-1≤ x -2≤1,∴1≤ x ≤3.故选D
角度3 已知函数单调性求参数的值或取值范围
例4[2023新高考卷Ⅰ]设函数 f ( x )=2 x ( x - a )在区间(0,1)单调递减,则 a 的取值范 围是( D)
命题点3 与函数的最值(值域)有关的问题
1.[2024河北省唐山市第二中学模拟]下列函数中,在区间(0,+∞)上单调递减的是( CC )
[解析] 因为 y =e x 是增函数, y =e- x 是减函数,所以 f ( x )=e x -e- x 在(0,+∞) 上单调递增,且 f ( x )>0.又 f ( x )=- x 2在(-∞,0]上单调递增,且 f ( x )≤0,所以 f ( x )在R上单调递增.又 c =lg20.9<0,0< b =lg32<1, a =50.01>1,即 a > b > c ,所以 f ( a )> f ( b )> f ( c ).
4.[多选/2024福建上杭一中模拟]高斯是德国著名数学家,有“数学王 子”的称号,他和阿基米德,牛顿并列为世界三大数学家,用[ x ]表示不超过 x 的最 大整数,则 y =[ x ]称为高斯函数,例如[-2.1]=-3,[2.1]=2.则下列说法正确的是 ( ACD )
5.[2024河南郑州模拟]函数 f ( x )=4 x -2 x +1-1的值域是 .
[解析] 由题知 f ( x )=(2 x )2-2·2 x -1,令2 x = t ( t >0),得 m ( t )= t 2-2 t -1=( t - 1)2-2( t >0),由于 m ( t )=( t -1)2-2( t >0)在(0,1)上单调递减,在(1,+∞)上单 调递增,所以 m ( t )≥ m (1)=-2,故 f ( x )的值域为[-2,+∞).
6. [2023贵州安顺模拟]若定义在R上的函数 f ( x ),对任意 x 1≠ x 2,都有 x 1 f ( x 1)+ x 2 f ( x 2)≥ x 1 f ( x 2)+ x 2 f ( x 1),则称 f ( x )为“ H 函数”.现给出下列函数,其中是“ H 函数”的有 .(填上所有正确答案的序号)
① f ( x )= x 2-2 x +3;
② f ( x )=2 x -1;
③ f ( x )=lg( x -1);
第18讲 导数与函数的极值、最值(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版): 这是一份第18讲 导数与函数的极值、最值(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共31页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,极大值点,极小值点,极小值,fx0,极值点等内容,欢迎下载使用。
第17讲 导数与函数的单调性(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版): 这是一份第17讲 导数与函数的单调性(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共30页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,大于0,小于0等内容,欢迎下载使用。
第15讲 函数模型的应用(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版): 这是一份第15讲 函数模型的应用(考点串讲课件)-2025年高考数学大一轮复习核心题型+易错重难点专项突破(新高考版),共38页。PPT课件主要包含了易混易错练,常用结论,知识梳理,考点分类练,最新模拟练,数学建模的过程,给出下列四个结论等内容,欢迎下载使用。












