第12讲 对数与对数函数（考点串讲课件）-2025年高考数学大一轮复习核心题型+易错重难点专项突破（新高考版）

这是一份第12讲 对数与对数函数（考点串讲课件）-2025年高考数学大一轮复习核心题型+易错重难点专项突破（新高考版），共33页。PPT课件主要包含了易混易错练，常用结论，知识梳理，考点分类练，最新模拟练，blogaN，常用对数，自然对数，换底公式，0+∞等内容，欢迎下载使用。

2.常用对数和自然对数(1)以10为底的对数称为　　　　　　　　,通常把lg10N简写为lg N. (2)以无理数e(e=2.718 28…)为底的对数称为　　　　　　　　,自然对数lgeN通常简写为　　　　. 
3.对数的性质与运算法则如果a>0,且a≠1,M>0,N>0,那么①lga(MN)=　　　　　　　　　; ②lga =　　　　　　　.
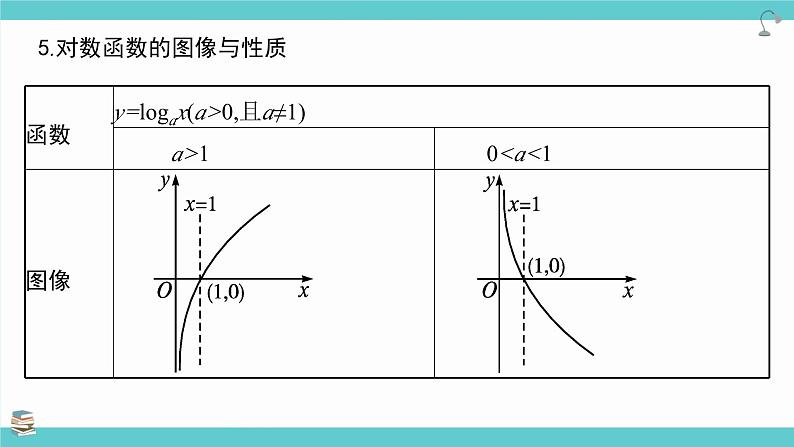
5.对数函数的图像与性质
6.反函数(1)一般地,如果在函数y=f(x)中,给定值域中任意一个y的值,只有唯一的x与之对应,那么x是y的函数,这个函数称为y=f(x)的反函数,记作y=f-1(x).(2)函数y=f(x)与它的反函数定义域和值域互换,图像关于直线　　　　对称. (3)指数函数y=ax(a>0且a≠1)与对数函数　　　　　　(a>0且a≠1)互为反函数. 
2.对数函数的图像与底数大小的比较如图,直线y=1与四个函数图像交点的横坐标即为相应的底数.结合图像知0易错点　忽略底数与真数的范围而致错
(1)转化：①利用 ab ＝ N ⇔ b ＝lg aN ( a ＞0且 a ≠1)对题目条件进行转化；②利用换底公式化为同底数的对数运算.
(3)拆分：将真数化为积、商或底数的指数幂形式，正用对数的运算性质化简
(4)合并：将对数式化为同底数对数的和、差、倍数的运算，然后逆用对数的运算性质，转化为同底数对数的真数的积、商、幂的运算.
例1 (1)[2022天津高考]化简(2lg43＋lg83)(lg32＋lg92)的值为(　B　)
(2)[2022浙江高考]已知2 a ＝5，lg83＝ b ，则4 a －3 b ＝(　C　)
命题点2　对数函数的图象及应用
与对数函数有关的图象问题的求解策略
1. 对于图象的识别，一般通过观察图象的变化趋势、利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.2. 对于对数型函数的图象，一般从最基本的对数函数的图象入手，通过平移、伸缩、对称变换而得到.
A　 　　　　 　B
C　　　 　　　　D
命题点3　对数函数的性质及应用
比较对数值大小的常用方法
1. 底数相同时，比较真数的大小；真数相同时，利用换底公式转化为底数相同的形式，再比较大小，也可以借助对数函数的图象比较大小.2. 当底数和真数都不相同时，常借助0，1或题干中出现的有理数等中间量比较大小，也可以通过作差或者作商比较大小.
3. (1)lg a f ( x )＝ b ⇔ f ( x )＝ ab ( a ＞0，且 a ≠1).
(2)lg af ( x )＝lg ag ( x )⇔ f ( x )＝ g ( x )( f ( x )＞0， g ( x )＞0).
4. 解简单对数不等式，先统一底数，化为形如lg a f ( x )＞lg ag ( x )的不等式，再借助 y ＝lg ax 的单调性求解
5.对数型复合函数的单调性问题的求解策略
(1)对于 y ＝lg a f ( x )型的复合函数的单调性，有以下结论：函数 y ＝lg a f ( x )的单调性与函数 u ＝ f ( x )( f ( x )＞0)的单调性在 a ＞1时相同，在0＜ a ＜1时相反.
(2)研究 y ＝ f (lg ax )型的复合函数的单调性，一般用换元法，即令 t ＝lg ax ，则只需研究 t ＝lg ax 及 y ＝ f ( t )的单调性即可.
注意　 研究对数型复合函数的单调性，一定要坚持“定义域优先”原则，否则所得范围易出错.
角度2　解对数方程或不等式
例4 (1)[2024湘豫名校联考]已知函数 f ( x )＝lg2｜ x ｜＋ x 2，则不等式 f (ln x )＋ f (－ln x )＜2的解集为(　D　)
角度3　对数函数性质的应用例5 (1)[全国卷Ⅱ]设函数 f ( x )＝ln｜2 x ＋1｜－ln｜2 x －1｜，则 f ( x )(　D　)
(2)[全国卷Ⅰ]若2 a ＋lg2 a ＝4 b ＋2lg4 b ，则(　B　)
[解析]　令 f ( x )＝2 x ＋lg2 x ，因为 y ＝2 x 在(0，＋∞)上单调递增， y ＝lg2 x 在(0， ＋∞)上单调递增，所以 f ( x )＝2 x ＋lg2 x 在(0，＋∞)上单调递增.又2 a ＋lg2 a ＝4 b ＋2lg4 b ＝22 b ＋lg2 b ＜22 b ＋lg2(2 b )，所以 f ( a )＜ f (2 b )，所以 a ＜2 b .故选B.
1. [2023宁夏六盘山高级中学模拟]若 f ( x )满足对定义域内任意的 x 1， x 2，都有 f ( x 1)＋ f ( x 2)＝ f ( x 1· x 2)，则称 f ( x )为“好函数”，则下列函数是“好函数”的是(　D　)
[解析]　因为lg3 x 1＋lg3 x 2＝lg3 x 1 x 2，满足 f ( x 1)＋ f ( x 2)＝ f ( x 1· x 2)，所以 f ( x )＝ lg3 x 是“好函数”，故选D.
3.[2024四川成都模拟]已知 a ＝lg0.70.3， b ＝lg0.30.7， c ＝0.5，则 a ， b ， c 的大小 关系为(　D　)
4.[2024河北石家庄市第十五中学模拟]已知函数 f ( x )＝lg( x 2－ ax ＋12)在[－1，3]上 单调递减，则实数 a 的取值范围是(　B　)
5.[2024陕西咸阳模拟]已知 a ＝2－0.01， b ＝lg510， c ＝lg612，则 a ， b ， c 的大小 关系为(　A　)