高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题31《函数的应用(二)》单元测试(A)(原卷版+解析)

这是一份高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题31《函数的应用(二)》单元测试(A)(原卷版+解析)，共17页。试卷主要包含了若，则实数的值是______.，的数据如下表，下列函数有零点的是等内容，欢迎下载使用。

命题范围：
第一章，第二章，第三章，第四章.
高考真题：
1．（2021·全国·高考真题（文））青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录表的数据V的满足．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（ ）（）
A．1.5B．1.2C．0.8D．0.6
2．（2020·北京·高考真题）函数的定义域是____________．
3．（2020·山东·高考真题）若，则实数的值是______.
牛刀小试
第I卷 选择题部分（共60分）
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（2022·全国·高一课时练习）设在区间上是连续变化的单调函数，且，则方程在内（ ）
A．至少有一实根B．至多有一实根
C．没有实根D．必有唯一实根
2．（2022·北京市第四十四中学高一期中）函数的零点个数是（ ）
A．0B．1C．2D．3
3．（2022·全国·高一课时练习）用二分法求函数的一个零点的近似值（误差不超过）时，依次计算得到如下数据：，，，，关于下一步的说法正确的是（ ）
A．已经达到对误差的要求，可以取作为近似值
B．已经达到对误差的要求，可以取作为近似值
C．没有达到对误差的要求，应该接着计算
D．没有达到对误差的要求，应该接着计算
4．（2022·全国·高一课时练习）据统计，第x年到鄱阳湖国家湿地公园越冬的白鹤数量y（只）近似满足.观测发现第1年有越冬白鹤3000只，估计第7年有越冬白鹤（ ）
A．4000只B．5000只 C．6000只 D．7000只
5．（2022·山东·淄博职业学院高一阶段练习）若二次函数与x轴没有公共点，则k的范围是（ ）
A．k>3B．k>C．k6．（2020·陕西·榆林市第十中学高一期中）某地西红柿从2月1日起开始上市.通过市场调查，得到西红柿种植成本单位：元与上市时间（单位：天）的数据如下表：
由表知，体现与数据关系的最佳函数模型是（ ）A．B．
C．D．
7．（2022·北京育才学校高一期中）函数的零点所在区间是（ ）
A．B．C．D．
8．（2022·贵州·高二开学考试）为了研究疫情有关指标的变化，现有学者给出了如下的模型：假定初始时刻的病例数为，平均每个病人可传染给个人，平均每个病人可以直接传染给其他人的时间为天，在天之内，病例数目的增长随时间（单位：天）的关系式为．若，则利用此模型预测第6天的病例数大约为1545．由此可知的值约为（参考数据：，，）（ ）
A．3.41B．3.40C．2.41D．2.40
二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得3分，有选错的得0分.
9．（2021·全国·高一课时练习）下列函数有零点的是( )
A．f(x)＝0B．f(x)＝2
C．f(x)＝－1D．f(x)＝x－
10．（2022·福建福州·高一期中）已知函数，则函数的零点是（ ）
A．-1B．0C．1D．2
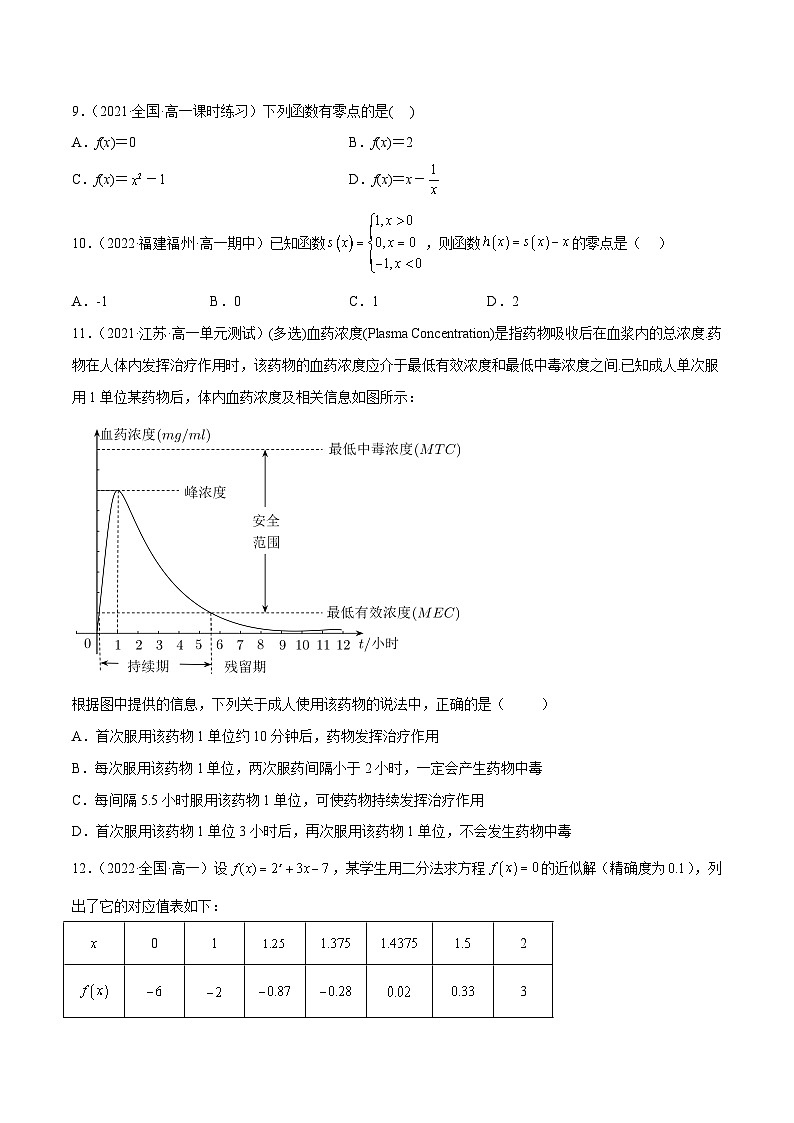
11．（2021·江苏·高一单元测试）(多选)血药浓度(Plasma Cncentratin)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时，该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后，体内血药浓度及相关信息如图所示：
根据图中提供的信息，下列关于成人使用该药物的说法中，正确的是（ ）
A．首次服用该药物1单位约10分钟后，药物发挥治疗作用
B．每次服用该药物1单位，两次服药间隔小于2小时，一定会产生药物中毒
C．每间隔5.5小时服用该药物1单位，可使药物持续发挥治疗作用
D．首次服用该药物1单位3小时后，再次服用该药物1单位，不会发生药物中毒
12．（2022·全国·高一）设，某学生用二分法求方程的近似解（精确度为），列出了它的对应值表如下：
若依据此表格中的数据，则得到符合要求的方程的近似解可以为（ ）
A．1.31B．1.38C．1.43D．1.44
第II卷 非选择题部分（共90分）
三、填空题：本大题共4小题，每小题5分，共20分.
13．（2022·北京育才学校高一期中）“定义在R上的函数满足，且在区间上存在零点”请写出一个符合要求的函数是______．
14．（2022·江苏·徐州市王杰中学高一阶段练习）函数的零点是___．
15．（2022·北京市昌平区第二中学高一期中）已知函数的两个零点分别为和，则的值为______．
16．（2021·黑龙江·佳木斯一中高一阶段练习）在某种新型材料的研制中，实验人员获得了如下一组实验数据：
现准备用下列四个函数中的一个近似地描述这些数据的规律：①；②；③；④其中最接近的一个是 _______ （只填序号）
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（2021·广西柳州·高一阶段练习）一种放射性物质不断变化为其他物质，每经过一年剩留的质量约是原来的75%，大约经过多少年，该物质的剩留量是原来的？
（参考数据：，）
18．（2021·全国·高一课前预习）求下列函数的零点：
(1)；
(2).
19．（2021·江苏·高一课时练习）某种细胞分裂时，由1个分裂成2个，2个分裂成4个……依此类推，写出这样的一个细胞分裂x次后，得到的细胞个数y与分裂次数x之间的函数关系式
20．（2021·全国·高一课时练习）如图，y＝f(x)反映了某公司产品的销售收入y万元与销售量x吨的函数关系，y＝g(x)反映了该公司产品的销售成本与销售量的函数关系，试问：
(1)当销售量为多少时，该公司赢利(收入大于成本)?
(2)当销售量为多少时，该公司亏损(收入小于成本)?
21．（2022·湖南·高一课时练习）1986年切尔诺贝利（现属乌克兰）发电厂的放射性物质泄漏到大气中，奥地利被碘131污染（半衰期8天），当碘131的含量为10%时将干草喂给奶牛是安全的．那么农民需要等待多久才能使用这些干草？
22．（2019·广东汕头·高一期末）汕头市某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.
（1）求商家降价前每星期的销售利润为多少元？
（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？
时间
50
120
150
种植成本
2600
500
2600
0
1
2
3
x
2
2.99
4
5
6.002
y
4
8.02
15.99
32
64.01
第四章 专题31 《函数的应用（二）》(A）
命题范围：
第一章，第二章，第三章，第四章.
高考真题：
1．（2021·全国·高考真题（文））青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录表的数据V的满足．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（ ）（）
A．1.5B．1.2C．0.8D．0.6
【答案】C
【分析】根据关系，当时，求出，再用指数表示，即可求解.
【详解】由，当时，，
则.
故选：C.
2．（2020·北京·高考真题）函数的定义域是____________．
【答案】
【分析】根据分母不为零、真数大于零列不等式组，解得结果.
【详解】由题意得，
故答案为：
3．（2020·山东·高考真题）若，则实数的值是______.
【答案】
【分析】根据对数运算化简为，求解的值.
【详解】，
即，解得：.
故答案为：
牛刀小试
第I卷 选择题部分（共60分）
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（2022·全国·高一课时练习）设在区间上是连续变化的单调函数，且，则方程在内（ ）
A．至少有一实根B．至多有一实根
C．没有实根D．必有唯一实根
【答案】D
【分析】根据零点存在性定理及函数的单调性判断即可.
【详解】解：因为在区间上连续的单调函数，且，
所以函数的图象在内与轴只有一个交点，即方程在内只有一个实根．
故选：D
2．（2022·北京市第四十四中学高一期中）函数的零点个数是（ ）
A．0B．1C．2D．3
【答案】C
【分析】利用方程法分别求出当、时函数的零点，进而即可求解.
【详解】当时，令，解得；
当时，令，解得.
所以函数有2个零点.
故选：C.
3．（2022·全国·高一课时练习）用二分法求函数的一个零点的近似值（误差不超过）时，依次计算得到如下数据：，，，，关于下一步的说法正确的是（ ）
A．已经达到对误差的要求，可以取作为近似值
B．已经达到对误差的要求，可以取作为近似值
C．没有达到对误差的要求，应该接着计算
D．没有达到对误差的要求，应该接着计算
【答案】C
【分析】由零点存在定理可知在内有零点，采用二分法可确定结果.
【详解】，在内有零点；
，
没有达到对误差的要求，应该继续计算.
故选：C.
4．（2022·全国·高一课时练习）据统计，第x年到鄱阳湖国家湿地公园越冬的白鹤数量y（只）近似满足.观测发现第1年有越冬白鹤3000只，估计第7年有越冬白鹤（ ）
A．4000只B．5000只 C．6000只 D．7000只
【答案】C
【分析】将代入表达式得，再将代入计算即可.
【详解】解：由题意，得，得，
所以当时，.
故选：C.
5．（2022·山东·淄博职业学院高一阶段练习）若二次函数与x轴没有公共点，则k的范围是（ ）
A．k>3B．k>C．k【答案】B
【分析】根据判别式即可求解.
【详解】是开口向上的二次函数，若与x轴没有公共点，则，因此 ，
故选：B
6．（2020·陕西·榆林市第十中学高一期中）某地西红柿从2月1日起开始上市.通过市场调查，得到西红柿种植成本单位：元与上市时间（单位：天）的数据如下表：
由表知，体现与数据关系的最佳函数模型是（ ）A．B．
C．D．
【答案】B
【分析】由提供的数据知，描述西红柿种植成本Q与上市时间t的变化关系函数不可能是单调函数，故可求得．
【详解】由提供的数据知，描述西红柿种植成本Q与上市时间t的变化关系函数不可能是常数函数，
也不是单调函数；而A，C，D对应的函数，在时，均为单调函数，
这与表格提供的数据不吻合，所以，选取B，
故选：B．
7．（2022·北京育才学校高一期中）函数的零点所在区间是（ ）
A．B．C．D．
【答案】B
【分析】本题考查函数零点存在性定理，满足，即零点在区间.
【详解】,
所以在单调递增，
因为

所以由零点存在性质定理知，的零点在.
故选：B
8．（2022·贵州·高二开学考试）为了研究疫情有关指标的变化，现有学者给出了如下的模型：假定初始时刻的病例数为，平均每个病人可传染给个人，平均每个病人可以直接传染给其他人的时间为天，在天之内，病例数目的增长随时间（单位：天）的关系式为．若，则利用此模型预测第6天的病例数大约为1545．由此可知的值约为（参考数据：，，）（ ）
A．3.41B．3.40C．2.41D．2.40
【答案】D
【分析】运用所给的关系式，结合代入法进行求解即可.
【详解】．
故选：D．
二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得3分，有选错的得0分.
9．（2021·全国·高一课时练习）下列函数有零点的是( )
A．f(x)＝0B．f(x)＝2
C．f(x)＝－1D．f(x)＝x－
【答案】ACD
【分析】令函数值为零，判断方程是否有解即可﹒
【详解】A：f(x)＝0，零点有无数多个；
B：函数f(x)＝2，对任意x∈R，不能满足方程f(x)＝0，因此函数f(x)＝2没有零点；
C：－1＝0有解，∴函数有零点；
D：x－＝0有解，∴函数有零点﹒
故选：ACD﹒
10．（2022·福建福州·高一期中）已知函数，则函数的零点是（ ）
A．-1B．0C．1D．2
【答案】ABC
【分析】令，根据的范围求解即可．
【详解】令，
当时，有，则；
当时，有，则；
当时，有，则；
故函数的零点是
故选：ABC
11．（2021·江苏·高一单元测试）(多选)血药浓度(Plasma Cncentratin)是指药物吸收后在血浆内的总浓度.药物在人体内发挥治疗作用时，该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间.已知成人单次服用1单位某药物后，体内血药浓度及相关信息如图所示：
根据图中提供的信息，下列关于成人使用该药物的说法中，正确的是（ ）
A．首次服用该药物1单位约10分钟后，药物发挥治疗作用
B．每次服用该药物1单位，两次服药间隔小于2小时，一定会产生药物中毒
C．每间隔5.5小时服用该药物1单位，可使药物持续发挥治疗作用
D．首次服用该药物1单位3小时后，再次服用该药物1单位，不会发生药物中毒
【答案】ABC
【分析】通过图象判断选项ABC正确；第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后，一定会发生药物中毒，故选项D错误.
【详解】从图象中可以看出，首次服用该药物1单位约10分钟后药物发挥治疗作用，故选项A正确；
根据图象可知，首次服用该药物1单位约1小时后的血药浓度达到最大值，由图象可知两次服药间隔小于2小时，一定会产生药物中毒，故选项B正确；
服药5.5小时时，血药浓度等于最低有效浓度，此时再服药，血药浓度增加，可使药物持续发挥治疗作用，故选项C正确；
第一次服用该药物1单位3小时后与第2次服用该药物1单位1小时后，血药浓度之和大于最低中毒浓度，因此一定会发生药物中毒，故选项D错误.
故选：ABC.
12．（2022·全国·高一）设，某学生用二分法求方程的近似解（精确度为），列出了它的对应值表如下：
若依据此表格中的数据，则得到符合要求的方程的近似解可以为（ ）
A．1.31B．1.38C．1.43D．1.44
【答案】BC
【分析】f(x)在R上是增函数，根据零点存在性定理进行判断零点所在的区间﹒
【详解】与都是上的单调递增函数，
是上的单调递增函数，
在上至多有一个零点，
由表格中的数据可知：
，
在上有唯一零点，零点所在的区间为，
即方程有且仅有一个解，且在区间内，
，
内的任意一个数都可以作为方程的近似解，
，
符合要求的方程的近似解可以是和1.43﹒
故选：BC﹒
第II卷 非选择题部分（共90分）
三、填空题：本大题共4小题，每小题5分，共20分.
13．（2022·北京育才学校高一期中）“定义在R上的函数满足，且在区间上存在零点”请写出一个符合要求的函数是______．
【答案】（答案不唯一）
【分析】根据题意结合零点定义分析求解.
【详解】的零点为，且满足，
故符合题意.
故答案为：（答案不唯一）.
14．（2022·江苏·徐州市王杰中学高一阶段练习）函数的零点是___．
【答案】8
【分析】根据零点定义解方程可得.
【详解】由得，解得，即的零点为8.
故答案为：8
15．（2022·北京市昌平区第二中学高一期中）已知函数的两个零点分别为和，则的值为______．
【答案】18
【分析】根据函数零点的定义以及韦达定理可得结果.
【详解】因为函数的两个零点分别为和，
所以和是的两个实根，
所以，，
所以.
故答案为：18.
16．（2021·黑龙江·佳木斯一中高一阶段练习）在某种新型材料的研制中，实验人员获得了如下一组实验数据：
现准备用下列四个函数中的一个近似地描述这些数据的规律：①；②；③；④其中最接近的一个是 _______ （只填序号）
【答案】④
【分析】将分别带入①②③④，即可得出答案.
【详解】
由表格数据可知其中最接近的一个是④.
故答案为：④.
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（2021·广西柳州·高一阶段练习）一种放射性物质不断变化为其他物质，每经过一年剩留的质量约是原来的75%，大约经过多少年，该物质的剩留量是原来的？
（参考数据：，）
【答案】4
【分析】设这种放射性物质的最初质量为1，经过年后，剩留量为，则有，然后根据题意可列方程进行求解即可
【详解】设这种放射性物质的最初质量为1，经过年后，剩留量为，则有，
由题意得，
即，
所以大约经过4年，该物质的剩留量是原来的
18．（2021·全国·高一课前预习）求下列函数的零点：
(1)；
(2).
【答案】(1)3；
(2)1﹒
【分析】(1)令y＝0直接求解即可；
(2)令f(x)＝0直接求解即可.
(1)
令y＝0，即，解得
∵∴函数的零点是3.
(2)
令，即，解得，∴函数的零点为1.
19．（2021·江苏·高一课时练习）某种细胞分裂时，由1个分裂成2个，2个分裂成4个……依此类推，写出这样的一个细胞分裂x次后，得到的细胞个数y与分裂次数x之间的函数关系式
【答案】
【分析】由题意知该函数模型为指数函数，设函数解析数为且，求得a的值，即可得出答案.
【详解】解：由题意知该函数模型为指数函数，设函数解析数为且，
当时，，所以，
所以.
20．（2021·全国·高一课时练习）如图，y＝f(x)反映了某公司产品的销售收入y万元与销售量x吨的函数关系，y＝g(x)反映了该公司产品的销售成本与销售量的函数关系，试问：
(1)当销售量为多少时，该公司赢利(收入大于成本)?
(2)当销售量为多少时，该公司亏损(收入小于成本)?
【答案】(1)销售量范围为；
(2)销售量范围为.
【分析】根据收入函数与成本函数的图象判断公司赢利或亏损时，对应销售量范围即可.
(1)
由图知：销售量大于a吨，即时，即公司赢利.
(2)
由图知：当销售量小于a吨，即时，即公司亏损.
21．（2022·湖南·高一课时练习）1986年切尔诺贝利（现属乌克兰）发电厂的放射性物质泄漏到大气中，奥地利被碘131污染（半衰期8天），当碘131的含量为10%时将干草喂给奶牛是安全的．那么农民需要等待多久才能使用这些干草？
【答案】天
【分析】设农民需要等待天才能使用这些干草，得到方程，结合对数的运算性质，即可求解.
【详解】设农民需要等待天才能使用这些干草，
根据题意得，可得，
所以农民需要等待大约天才能使用这些干草.
22．（2019·广东汕头·高一期末）汕头市某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.
（1）求商家降价前每星期的销售利润为多少元？
（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？
【答案】（1）2400（元）；（2）应将售价定为125元，最大销售利润是2500元.
【分析】（1）由销售利润=单件成本×销售量，即可求商家降价前每星期的销售利润；
（2）由题意得，根据二次函数的性质即可知最大销售利润及对应的售价.
【详解】（1）由题意，商家降价前每星期的销售利润为（元）；
（2）设售价定为元，则销售利润.
当时，有最大值2500.
∴应将售价定为125元，最大销售利润是2500元.
时间
50
120
150
种植成本
2600
500
2600
0
1
2
3
x
2
2.99
4
5
6.002
y
4
8.02
15.99
32
64.01
x
2
2.99
4
5
6.002
y
4
8.02
15.99
32
64.01
①
4
5.98
8
10
120.04
②
1.5
3.97
7.5
12
1800.70
③
1
1.58
2
2.32
5.91
④
4
7.94
16
32
64