

还剩12页未读,
继续阅读
成套系列资料,整套一键下载
- 高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题15函数的基本性质单元测试(A)(原卷版+解析) 试卷 0 次下载
- 高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题16函数的基本性质单元测试(B)(原卷版+解析) 试卷 0 次下载
- 高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题18幂函数单元测试(B)(原卷版+解析) 试卷 0 次下载
- 高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题19函数的应用(一)单元测试(A)(原卷版+解析) 试卷 0 次下载
- 高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题20函数的应用(一)单元测试(B)(原卷版+解析) 试卷 0 次下载
高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题17幂函数单元测试(A)(原卷版+解析)
展开
这是一份高中数学人教A版2019必修第一册同步单元测试AB卷(新高考)专题17幂函数单元测试(A)(原卷版+解析),共15页。试卷主要包含了函数的图象是等内容,欢迎下载使用。
命题范围:
第一章,第二章,函数的概念及其表示方法,函数的基本性质,幂函数.
高考真题:
1.(2011·上海·高考真题(文))下列函数中,既是偶函数,又是在区间上单调递减的函数为( )
A.B.C.D.
2.(2011·陕西·高考真题(文))函数的图象是
A.B.
C.D.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是____.
牛刀小试
第I卷 选择题部分(共60分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2022·全国·高一课时练习)函数的图象大致为( )
A.B.
C.D.
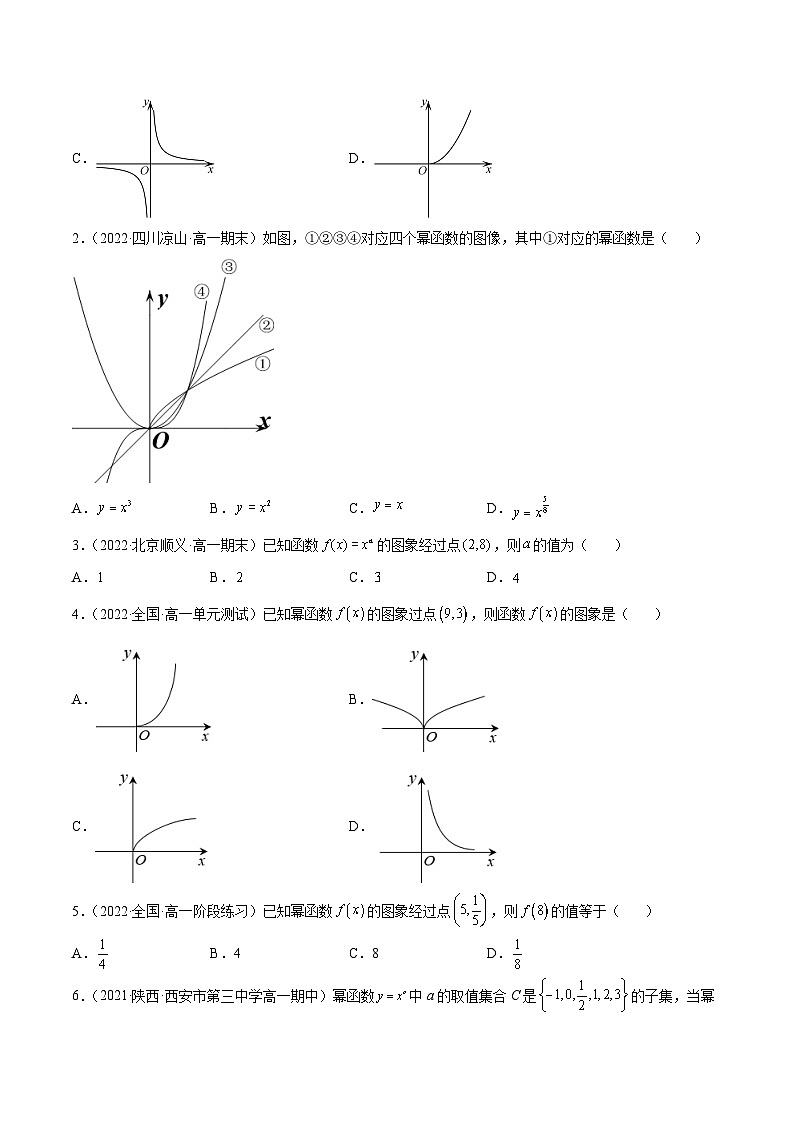
2.(2022·四川凉山·高一期末)如图,①②③④对应四个幂函数的图像,其中①对应的幂函数是( )
A.B.C.D.
3.(2022·北京顺义·高一期末)已知函数的图象经过点,则的值为( )
A.B.C.D.
4.(2022·全国·高一单元测试)已知幂函数的图象过点,则函数的图象是( )
A.B.
C.D.
5.(2022·全国·高一阶段练习)已知幂函数的图象经过点,则的值等于( )
A.B.4C.8D.
6.(2021·陕西·西安市第三中学高一期中)幂函数中a的取值集合C是的子集,当幂函数的值域与定义域相同时,集合C为( )
A.B.C.D.
7.(2022·全国·高一课时练习)已知幂函数为偶函数,则实数的值为( )
A.3B.2C.1D.1或2
8.(2022·全国·高一课时练习)下列命题正确的是( )
A.幂函数的图象都经过,两点B.函数的图象经过第二象限
C.如果两个幂函数的图象有三个公共点,那么这两个函数一定相同D.如果幂函数为偶函数,则图象一定经过点
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.(2020·湖南·嘉禾县第一中学高一阶段练习)下列函数为幂函数的是( )
A.B.
C.D.
10.(2021·全国·高一专题练习)已知幂函数,则是( )
A.偶函数B.奇函数C.有最大值D.无最大值
11.(2022·广东·韶关市田家炳中学高一期末)如果幂函数的图象不过原点,则实数的取值为( )
A.B.C.D.无解
12.(2022·全国·高一)下列关于幂函数的性质说法正确的有( )
A.当时,函数在其定义域上递减
B.当时,函数图象是一条直线
C.当时,函数是偶函数
D.当时,函数的图象与轴交点的横坐标为
第II卷 非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.(2021·上海市杨浦高级中学高一期中)幂函数的定义域为______;
14.(2022·全国·高一课时练习)若函数是幂函数,则实数______.
15.(2022·全国·高一课时练习)已知幂函数的图像过点,则___________.
16.(2022·江西赣州·高一期末)已知幂函数在区间上单调递减,则实数的值为______.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2021·全国·高一课前预习)已知是幂函数,求、的值.
18.(2021·江苏·高一课时练习)分别写出下列函数的定义域,并指出它们的奇偶性:
(1);
(2);
(3);
(4).
19.(2021·全国·高一课时练习)已知幂函数的图象过点,试求出这个函数的解析式.
20.(2021·全国·高一课时练习)比较下列各组中两个数的大小.
(1),;
(2),.
21.(2021·江苏·高一课时练习)函数y=(m2-m-1)是幂函数,且在x∈上为减函数,求实数m的值.
22.(2020·江苏·高一课时练习)若,求实数a的取值范围.
第三章 专题17 幂函数(A)
命题范围:
第一章,第二章,函数的概念及其表示方法,函数的基本性质,幂函数.
高考真题:
1.(2011·上海·高考真题(文))下列函数中,既是偶函数,又是在区间上单调递减的函数为( )
A.B.C.D.
【答案】A
【详解】试题分析:由偶函数定义知,仅A,C为偶函数, C. 在区间上单调递增函数,故选A.
2.(2011·陕西·高考真题(文))函数的图象是
A.B.
C.D.
【答案】B
【详解】试题分析:先找出函数图象上的特殊点(1,1),(8,2),(,),再判断函数的走向,结合图形,选出正确的答案.
解:函数图象上的特殊点(1,1),故排除A,D;
由特殊点(8,2),(,),可排除C.
故选B.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是____.
【答案】
【分析】先求,再根据奇函数求
【详解】,因为为奇函数,所以
故答案为:
牛刀小试
第I卷 选择题部分(共60分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2022·全国·高一课时练习)函数的图象大致为( )
A.B.
C.D.
【答案】C
【分析】首先得到函数的定义域,再判断函数的奇偶性,最后根据幂函数的性质判断即可;
【详解】解:因为,即,定义域为,且,
即为奇函数,又由幂函数的性质可知在上单调递减,
所以在上单调递减,故符合题意的只有C;
故选:C
2.(2022·四川凉山·高一期末)如图,①②③④对应四个幂函数的图像,其中①对应的幂函数是( )
A.B.C.D.
【答案】D
【分析】根据函数图象求出幂函数的指数取值范围,得到正确答案.
【详解】根据函数图象可得:①对应的幂函数在上单调递增,且增长速度越来越慢,故,故D选项符合要求.
故选:D
3.(2022·北京顺义·高一期末)已知函数的图象经过点,则的值为( )
A.B.C.D.
【答案】C
【分析】将点的坐标代入函数解析式,求出的值即可.
【详解】因为函数的图象经过点,
所以,则.
故选:C.
4.(2022·全国·高一单元测试)已知幂函数的图象过点,则函数的图象是( )
A.B.
C.D.
【答案】C
【分析】设出函数的解析式,根据幂函数的图象过点,构造方程求出指数的值,再结合函数的解析式研究其性质即可得到图象.
【详解】设幂函数的解析式为,
∵幂函数的图象过点,
∴,
解得
∴,其定义域为,且是增函数,
当时,其图象在直线的上方.对照选项可知C满足题意.
故选:C.
5.(2022·全国·高一阶段练习)已知幂函数的图象经过点,则的值等于( )
A.B.4C.8D.
【答案】D
【分析】设幂函数,由题设条件可求,从而可求的值.
【详解】设幂函数,幂函数的图象经过点,所以,
解得,所以,则.
故选:D.
6.(2021·陕西·西安市第三中学高一期中)幂函数中a的取值集合C是的子集,当幂函数的值域与定义域相同时,集合C为( )
A.B.C.D.
【答案】C
【分析】分别求出各幂函数的定义域和值域,得到答案.
【详解】当时,定义域和值域均为,符合题意;
时,定义域为,值域为,故不合题意;
时,定义域为,值域为,符合题意;
时,定义域与值域均为R,符合题意;
时,定义域为R,值域为,不符合题意;
时,定义域与值域均为R,符合题意.
故选:C
7.(2022·全国·高一课时练习)已知幂函数为偶函数,则实数的值为( )
A.3B.2C.1D.1或2
【答案】C
【分析】由题意利用幂函数的定义和性质,得出结论.
【详解】幂函数为偶函数,
,且为偶数,
则实数,
故选:C
8.(2022·全国·高一课时练习)下列命题正确的是( )
A.幂函数的图象都经过,两点B.函数的图象经过第二象限
C.如果两个幂函数的图象有三个公共点,那么这两个函数一定相同D.如果幂函数为偶函数,则图象一定经过点
【答案】D
【分析】通过举反例可判断A、C项,根据幂函数的性质可判断B项,根据幂函数的性质集合偶函数的定义可判断D项.
【详解】解:对于A,幂函数的图象都经过点,当时,不过点,故A项错误;
对于B,的图象过第一、三象限,故B项错误;
对于C,与的图象有三个交点,这两个函数不相同,故C项错误;
对于D,因为幂函数的图象都经过点,所以幂函数为偶函数时,图象一定经过点,故D项正确.
故选:D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.(2020·湖南·嘉禾县第一中学高一阶段练习)下列函数为幂函数的是( )
A.B.
C.D.
【答案】BD
【分析】根据幂函数的定义可得结果.
【详解】由幂函数的定义知,函数,为幂函数.
故选:BD.
10.(2021·全国·高一专题练习)已知幂函数,则是( )
A.偶函数B.奇函数C.有最大值D.无最大值
【答案】BD
【分析】根据幂函数的定义,可知,从而得出函数,根据幂函数的图象和性质,即可得出答案.
【详解】解:由题可知,是幂函数,则,
所以,
所以是奇函数,且无最大值.
故选:BD.
11.(2022·广东·韶关市田家炳中学高一期末)如果幂函数的图象不过原点,则实数的取值为( )
A.B.C.D.无解
【答案】BC
【分析】利用已知条件可得出关于实数的等式与不等式,由此可解得实数的值.
【详解】由已知可得,解得或.
故选:BC.
12.(2022·全国·高一)下列关于幂函数的性质说法正确的有( )
A.当时,函数在其定义域上递减
B.当时,函数图象是一条直线
C.当时,函数是偶函数
D.当时,函数的图象与轴交点的横坐标为
【答案】CD
【分析】根据幂函数的性质,对每个选项进行逐一分析,即可判断和选择.
【详解】当时,,函数在(-∞,0)和(0,+∞)上递减,不能说在定义域上递减,故A选项错误;
当时,,,其图象是去掉点的直线,故B选项错误;
当时,,函数的定义域为,是偶函数,所以C选项正确;
当时,,其图象与轴只有个交点,且交点的横坐标为,所以D选项正确.
故选:CD.
第II卷 非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.(2021·上海市杨浦高级中学高一期中)幂函数的定义域为______;
【答案】
【分析】利用根式的性质求函数定义域.
【详解】由根式的性质知:,
所以函数定义域为.
故答案为:
14.(2022·全国·高一课时练习)若函数是幂函数,则实数______.
【答案】1
【分析】根据幂函数定义列方程求解可得.
【详解】因为是幂函数,所以,解得.
故答案为:1
15.(2022·全国·高一课时练习)已知幂函数的图像过点,则___________.
【答案】
【分析】根据幂函数的定义求解即可.
【详解】根据幂函数定义得,,所以,又图像过点,
所以,解得,所以.
故答案为:.
16.(2022·江西赣州·高一期末)已知幂函数在区间上单调递减,则实数的值为______.
【答案】
【分析】根据幂函数的概念,求得,再结合幂函数的性质,即可求解.
【详解】由题意,幂函数,可得,解得或,
当时,函数在区间上单调递增,不符合题意;
当时,函数在区间上单调递减,符合题意,
所以实数的值为-.
故答案为:-.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2021·全国·高一课前预习)已知是幂函数,求、的值.
【答案】;.
【分析】根据幂函数的定义即可列方程组求解.
【详解】由题意得解得
.
18.(2021·江苏·高一课时练习)分别写出下列函数的定义域,并指出它们的奇偶性:
(1);
(2);
(3);
(4).
【答案】答案见解析.
【分析】直接观察出定义域,在根据和的关系来判断单调性.
【详解】(1),其定义域为R,
又,
故为定义域为R的偶函数;
(2),其定义域为,其为非奇非偶函数;
(3),其定义域为,
又,
故为定义域为的奇函数;
(4),其定义域为R,
又,
故为定义域为R的偶函数.
19.(2021·全国·高一课时练习)已知幂函数的图象过点,试求出这个函数的解析式.
【答案】
【分析】直接带点计算即可.
【详解】由已知,得,即.
20.(2021·全国·高一课时练习)比较下列各组中两个数的大小.
(1),;
(2),.
【答案】(1);(2)
【分析】(1)利用幂函数的单调性即可比较大小;
(2)利用幂函数的单调性即可比较大小.
【详解】(1)利用幂函数的性质.
幂函数在上是增函数,而,所以.
(2)利用幂函数的性质.
幂函数在定义域上是减函数,而,所以.
21.(2021·江苏·高一课时练习)函数y=(m2-m-1)是幂函数,且在x∈上为减函数,求实数m的值.
【答案】
【分析】根据幂函数的定义及单调性即可求解.
【详解】解:因为函数y=(m2-m-1)是幂函数, 所以m2-m-1=1,解得m=-1或m=2,
又函数y=(m2-m-1)在x∈上为减函数, 所以m-1<0,即m<1,
所以m=.
22.(2020·江苏·高一课时练习)若,求实数a的取值范围.
【答案】.
【解析】首先设幂函数,得到函数 为的增函数,再利用单调性解不等式即可.
【详解】解:由函数是定义在上的增函数,
若,
则,
解得:,
即实数a的取值范围为.
命题范围:
第一章,第二章,函数的概念及其表示方法,函数的基本性质,幂函数.
高考真题:
1.(2011·上海·高考真题(文))下列函数中,既是偶函数,又是在区间上单调递减的函数为( )
A.B.C.D.
2.(2011·陕西·高考真题(文))函数的图象是
A.B.
C.D.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是____.
牛刀小试
第I卷 选择题部分(共60分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2022·全国·高一课时练习)函数的图象大致为( )
A.B.
C.D.
2.(2022·四川凉山·高一期末)如图,①②③④对应四个幂函数的图像,其中①对应的幂函数是( )
A.B.C.D.
3.(2022·北京顺义·高一期末)已知函数的图象经过点,则的值为( )
A.B.C.D.
4.(2022·全国·高一单元测试)已知幂函数的图象过点,则函数的图象是( )
A.B.
C.D.
5.(2022·全国·高一阶段练习)已知幂函数的图象经过点,则的值等于( )
A.B.4C.8D.
6.(2021·陕西·西安市第三中学高一期中)幂函数中a的取值集合C是的子集,当幂函数的值域与定义域相同时,集合C为( )
A.B.C.D.
7.(2022·全国·高一课时练习)已知幂函数为偶函数,则实数的值为( )
A.3B.2C.1D.1或2
8.(2022·全国·高一课时练习)下列命题正确的是( )
A.幂函数的图象都经过,两点B.函数的图象经过第二象限
C.如果两个幂函数的图象有三个公共点,那么这两个函数一定相同D.如果幂函数为偶函数,则图象一定经过点
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.(2020·湖南·嘉禾县第一中学高一阶段练习)下列函数为幂函数的是( )
A.B.
C.D.
10.(2021·全国·高一专题练习)已知幂函数,则是( )
A.偶函数B.奇函数C.有最大值D.无最大值
11.(2022·广东·韶关市田家炳中学高一期末)如果幂函数的图象不过原点,则实数的取值为( )
A.B.C.D.无解
12.(2022·全国·高一)下列关于幂函数的性质说法正确的有( )
A.当时,函数在其定义域上递减
B.当时,函数图象是一条直线
C.当时,函数是偶函数
D.当时,函数的图象与轴交点的横坐标为
第II卷 非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.(2021·上海市杨浦高级中学高一期中)幂函数的定义域为______;
14.(2022·全国·高一课时练习)若函数是幂函数,则实数______.
15.(2022·全国·高一课时练习)已知幂函数的图像过点,则___________.
16.(2022·江西赣州·高一期末)已知幂函数在区间上单调递减,则实数的值为______.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2021·全国·高一课前预习)已知是幂函数,求、的值.
18.(2021·江苏·高一课时练习)分别写出下列函数的定义域,并指出它们的奇偶性:
(1);
(2);
(3);
(4).
19.(2021·全国·高一课时练习)已知幂函数的图象过点,试求出这个函数的解析式.
20.(2021·全国·高一课时练习)比较下列各组中两个数的大小.
(1),;
(2),.
21.(2021·江苏·高一课时练习)函数y=(m2-m-1)是幂函数,且在x∈上为减函数,求实数m的值.
22.(2020·江苏·高一课时练习)若,求实数a的取值范围.
第三章 专题17 幂函数(A)
命题范围:
第一章,第二章,函数的概念及其表示方法,函数的基本性质,幂函数.
高考真题:
1.(2011·上海·高考真题(文))下列函数中,既是偶函数,又是在区间上单调递减的函数为( )
A.B.C.D.
【答案】A
【详解】试题分析:由偶函数定义知,仅A,C为偶函数, C. 在区间上单调递增函数,故选A.
2.(2011·陕西·高考真题(文))函数的图象是
A.B.
C.D.
【答案】B
【详解】试题分析:先找出函数图象上的特殊点(1,1),(8,2),(,),再判断函数的走向,结合图形,选出正确的答案.
解:函数图象上的特殊点(1,1),故排除A,D;
由特殊点(8,2),(,),可排除C.
故选B.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是____.
【答案】
【分析】先求,再根据奇函数求
【详解】,因为为奇函数,所以
故答案为:
牛刀小试
第I卷 选择题部分(共60分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2022·全国·高一课时练习)函数的图象大致为( )
A.B.
C.D.
【答案】C
【分析】首先得到函数的定义域,再判断函数的奇偶性,最后根据幂函数的性质判断即可;
【详解】解:因为,即,定义域为,且,
即为奇函数,又由幂函数的性质可知在上单调递减,
所以在上单调递减,故符合题意的只有C;
故选:C
2.(2022·四川凉山·高一期末)如图,①②③④对应四个幂函数的图像,其中①对应的幂函数是( )
A.B.C.D.
【答案】D
【分析】根据函数图象求出幂函数的指数取值范围,得到正确答案.
【详解】根据函数图象可得:①对应的幂函数在上单调递增,且增长速度越来越慢,故,故D选项符合要求.
故选:D
3.(2022·北京顺义·高一期末)已知函数的图象经过点,则的值为( )
A.B.C.D.
【答案】C
【分析】将点的坐标代入函数解析式,求出的值即可.
【详解】因为函数的图象经过点,
所以,则.
故选:C.
4.(2022·全国·高一单元测试)已知幂函数的图象过点,则函数的图象是( )
A.B.
C.D.
【答案】C
【分析】设出函数的解析式,根据幂函数的图象过点,构造方程求出指数的值,再结合函数的解析式研究其性质即可得到图象.
【详解】设幂函数的解析式为,
∵幂函数的图象过点,
∴,
解得
∴,其定义域为,且是增函数,
当时,其图象在直线的上方.对照选项可知C满足题意.
故选:C.
5.(2022·全国·高一阶段练习)已知幂函数的图象经过点,则的值等于( )
A.B.4C.8D.
【答案】D
【分析】设幂函数,由题设条件可求,从而可求的值.
【详解】设幂函数,幂函数的图象经过点,所以,
解得,所以,则.
故选:D.
6.(2021·陕西·西安市第三中学高一期中)幂函数中a的取值集合C是的子集,当幂函数的值域与定义域相同时,集合C为( )
A.B.C.D.
【答案】C
【分析】分别求出各幂函数的定义域和值域,得到答案.
【详解】当时,定义域和值域均为,符合题意;
时,定义域为,值域为,故不合题意;
时,定义域为,值域为,符合题意;
时,定义域与值域均为R,符合题意;
时,定义域为R,值域为,不符合题意;
时,定义域与值域均为R,符合题意.
故选:C
7.(2022·全国·高一课时练习)已知幂函数为偶函数,则实数的值为( )
A.3B.2C.1D.1或2
【答案】C
【分析】由题意利用幂函数的定义和性质,得出结论.
【详解】幂函数为偶函数,
,且为偶数,
则实数,
故选:C
8.(2022·全国·高一课时练习)下列命题正确的是( )
A.幂函数的图象都经过,两点B.函数的图象经过第二象限
C.如果两个幂函数的图象有三个公共点,那么这两个函数一定相同D.如果幂函数为偶函数,则图象一定经过点
【答案】D
【分析】通过举反例可判断A、C项,根据幂函数的性质可判断B项,根据幂函数的性质集合偶函数的定义可判断D项.
【详解】解:对于A,幂函数的图象都经过点,当时,不过点,故A项错误;
对于B,的图象过第一、三象限,故B项错误;
对于C,与的图象有三个交点,这两个函数不相同,故C项错误;
对于D,因为幂函数的图象都经过点,所以幂函数为偶函数时,图象一定经过点,故D项正确.
故选:D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.
9.(2020·湖南·嘉禾县第一中学高一阶段练习)下列函数为幂函数的是( )
A.B.
C.D.
【答案】BD
【分析】根据幂函数的定义可得结果.
【详解】由幂函数的定义知,函数,为幂函数.
故选:BD.
10.(2021·全国·高一专题练习)已知幂函数,则是( )
A.偶函数B.奇函数C.有最大值D.无最大值
【答案】BD
【分析】根据幂函数的定义,可知,从而得出函数,根据幂函数的图象和性质,即可得出答案.
【详解】解:由题可知,是幂函数,则,
所以,
所以是奇函数,且无最大值.
故选:BD.
11.(2022·广东·韶关市田家炳中学高一期末)如果幂函数的图象不过原点,则实数的取值为( )
A.B.C.D.无解
【答案】BC
【分析】利用已知条件可得出关于实数的等式与不等式,由此可解得实数的值.
【详解】由已知可得,解得或.
故选:BC.
12.(2022·全国·高一)下列关于幂函数的性质说法正确的有( )
A.当时,函数在其定义域上递减
B.当时,函数图象是一条直线
C.当时,函数是偶函数
D.当时,函数的图象与轴交点的横坐标为
【答案】CD
【分析】根据幂函数的性质,对每个选项进行逐一分析,即可判断和选择.
【详解】当时,,函数在(-∞,0)和(0,+∞)上递减,不能说在定义域上递减,故A选项错误;
当时,,,其图象是去掉点的直线,故B选项错误;
当时,,函数的定义域为,是偶函数,所以C选项正确;
当时,,其图象与轴只有个交点,且交点的横坐标为,所以D选项正确.
故选:CD.
第II卷 非选择题部分(共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.(2021·上海市杨浦高级中学高一期中)幂函数的定义域为______;
【答案】
【分析】利用根式的性质求函数定义域.
【详解】由根式的性质知:,
所以函数定义域为.
故答案为:
14.(2022·全国·高一课时练习)若函数是幂函数,则实数______.
【答案】1
【分析】根据幂函数定义列方程求解可得.
【详解】因为是幂函数,所以,解得.
故答案为:1
15.(2022·全国·高一课时练习)已知幂函数的图像过点,则___________.
【答案】
【分析】根据幂函数的定义求解即可.
【详解】根据幂函数定义得,,所以,又图像过点,
所以,解得,所以.
故答案为:.
16.(2022·江西赣州·高一期末)已知幂函数在区间上单调递减,则实数的值为______.
【答案】
【分析】根据幂函数的概念,求得,再结合幂函数的性质,即可求解.
【详解】由题意,幂函数,可得,解得或,
当时,函数在区间上单调递增,不符合题意;
当时,函数在区间上单调递减,符合题意,
所以实数的值为-.
故答案为:-.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(2021·全国·高一课前预习)已知是幂函数,求、的值.
【答案】;.
【分析】根据幂函数的定义即可列方程组求解.
【详解】由题意得解得
.
18.(2021·江苏·高一课时练习)分别写出下列函数的定义域,并指出它们的奇偶性:
(1);
(2);
(3);
(4).
【答案】答案见解析.
【分析】直接观察出定义域,在根据和的关系来判断单调性.
【详解】(1),其定义域为R,
又,
故为定义域为R的偶函数;
(2),其定义域为,其为非奇非偶函数;
(3),其定义域为,
又,
故为定义域为的奇函数;
(4),其定义域为R,
又,
故为定义域为R的偶函数.
19.(2021·全国·高一课时练习)已知幂函数的图象过点,试求出这个函数的解析式.
【答案】
【分析】直接带点计算即可.
【详解】由已知,得,即.
20.(2021·全国·高一课时练习)比较下列各组中两个数的大小.
(1),;
(2),.
【答案】(1);(2)
【分析】(1)利用幂函数的单调性即可比较大小;
(2)利用幂函数的单调性即可比较大小.
【详解】(1)利用幂函数的性质.
幂函数在上是增函数,而,所以.
(2)利用幂函数的性质.
幂函数在定义域上是减函数,而,所以.
21.(2021·江苏·高一课时练习)函数y=(m2-m-1)是幂函数,且在x∈上为减函数,求实数m的值.
【答案】
【分析】根据幂函数的定义及单调性即可求解.
【详解】解:因为函数y=(m2-m-1)是幂函数, 所以m2-m-1=1,解得m=-1或m=2,
又函数y=(m2-m-1)在x∈上为减函数, 所以m-1<0,即m<1,
所以m=.
22.(2020·江苏·高一课时练习)若,求实数a的取值范围.
【答案】.
【解析】首先设幂函数,得到函数 为的增函数,再利用单调性解不等式即可.
【详解】解:由函数是定义在上的增函数,
若,
则,
解得:,
即实数a的取值范围为.












