






高三数学一轮复习第九章计数原理、概率、随机变量及其分布培优专题一5概率模型的辨识与应用课件
展开[培优技法] 高考常考的概率模型有相互独立事件的概率模型、二项分布模型、超几何分布模型和正态分布模型,其中二项分布与超几何分布模型的辨识一直是学生的难点和易错点.在有放回抽样时,每次抽取时的总体没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复试验,符合这一特征的随机变量服从二项分布;而不放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,符合这一特征的随机变量服从超几何分布.因此,二项分布与超几何分布最根本的区别在于是有放回抽样还是不放回抽样.下面就高考常考的四种概率模型予以辨识说明.
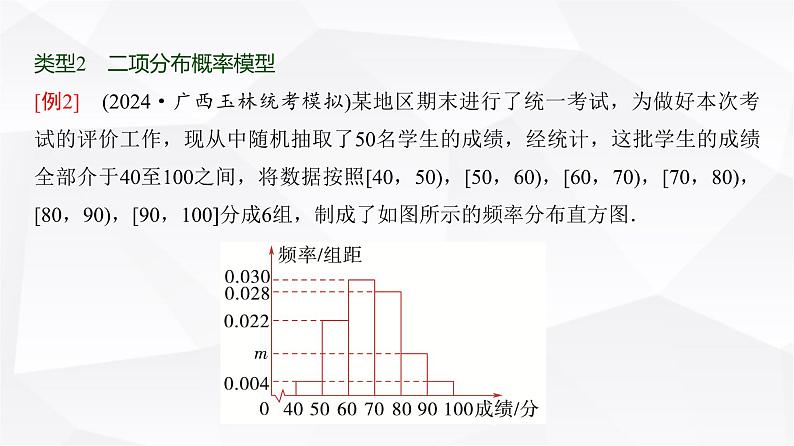
类型2 二项分布概率模型[例2] (2024·广西玉林统考模拟)某地区期末进行了统一考试,为做好本次考试的评价工作,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图所示的频率分布直方图.
点拨 二项分布概率模型的特征(1)在每一次试验中,试验结果只有两个,即发生与不发生;(2)各次试验中的事件是相互独立的;(3)在每一次试验中,事件发生的概率保持不变.
类型3 超几何分布概率模型[例3] (2024·河南安阳高三期末)不负青山,力换“金山”,民宿旅游逐渐成为一种热潮,山野乡村的民宿深受广大旅游爱好者的喜爱.某地区结合当地资源,按照“山上生态做减法、山下产业做加法”的思路,科学有序地发展环山文旅康养产业,温泉度假小镇、环山绿道、农家乐提档升级、特色民宿群等一批生态产业项目加快实施.为了在节假日接待好游客,该地旅游局对本地区各乡村的普通型民宿和品质型民宿进行了调研,随机抽取了10家乡村民宿,统计得到各家的房间数如下表:
(1)若旅游局随机从乙、丙2家各选2间民宿进行调研,求选出的4间均为普通型民宿的概率;(2)从这10家中随机抽取4家民宿,记其中普通型民宿的房间不低于17间的有X家,求X的分布列和数学期望.
点拨 超几何分布概率模型的特征(1)实际问题所描述的事件只包含两个结果(发生与不发生),每进行一次上述抽取都不是原来的重复(再次抽取时,都与上次条件发生了变化);(2)每次抽取中同一事件发生的概率都不同; (3)实际问题中随机变量为抽到某类个体的个数; (4)该问题属于不放回抽取问题.
类型4 正态分布概率模型[例4] 为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望.(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①试说明上述监控生产过程方法的合理性;②下面是检验员在一天内抽取的16个零件的尺寸:
[解] (1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 4,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 6,故X~B(16,0.002 6).因此P(X≥1)=1-P(X=0)=1-0.997 416≈0.040 8.X的数学期望E(X )=16×0.002 6=0.041 6.(2)①如果生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有0.002 6,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.040 8,发生的概率很小,因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.
新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第5讲 条件概率二项分布与正态分布(含解析): 这是一份新高考数学一轮复习课件第9章计数原理概率随机变量及其分布第5讲 条件概率二项分布与正态分布(含解析),共60页。PPT课件主要包含了条件概率,事件的相互独立性,全概率公式,2二项分布,正态分布,图9-7-1,题组一,走出误区,答案1×,2×3√等内容,欢迎下载使用。
新高考数学一轮复习专题九计数原理、概率与统计微专题一概率与函数综合问题课件: 这是一份新高考数学一轮复习专题九计数原理、概率与统计微专题一概率与函数综合问题课件,共12页。
2024届高考数学一轮总复习第九章计数原理概率随机变量及其分布第一讲分类加法计数原理与分步乘法计数原理课件: 这是一份2024届高考数学一轮总复习第九章计数原理概率随机变量及其分布第一讲分类加法计数原理与分步乘法计数原理课件,共34页。PPT课件主要包含了答案B,答案A,答案12,答案C,答案AC,答案336,答案7200,答案D,种不同的选择,两类计算等内容,欢迎下载使用。












