数学七年级上册6.2 直线、射线、线段教课内容ppt课件

这是一份数学七年级上册6.2 直线、射线、线段教课内容ppt课件，共29页。PPT课件主要包含了活动导入，情境导入，问题导入，线段最短，两点之间线段最短，尺规作图略，MN＝7cm，小组展示，我提问，我回答等内容，欢迎下载使用。

1. 通过学生自主探究，会用尺规作图，理解线段的长短、和、差、中点的几何意义及数量关系，并会用文字语言、图形语言、符号语言进行综合描述，提高学生的自主学习能力和语言描述能力．2．通过对图形的分析，会利用线段的和、差、中点等知识进行初步的推理与计算，体会分类讨论的思想，提高学生的推理能力．
同学们，请你在草稿纸上画一条线段AB.你能在草稿纸上作出一条同样大小的线段吗？你是怎么做的？
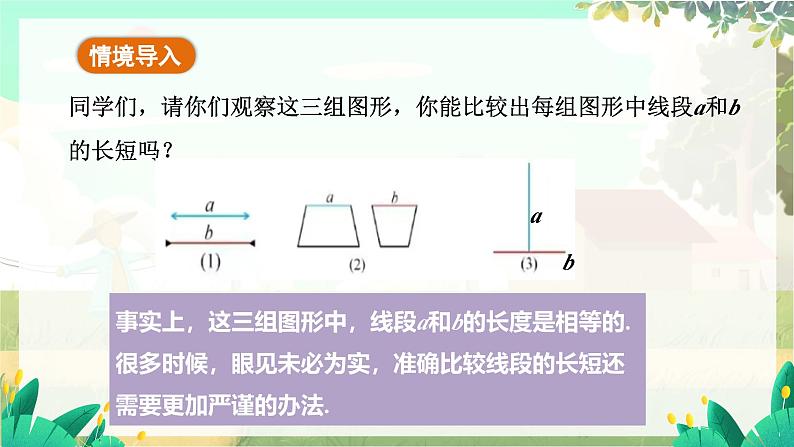
同学们，请你们观察这三组图形，你能比较出每组图形中线段a和b的长短吗？
事实上，这三组图形中，线段a和b的长度是相等的.很多时候，眼见未必为实，准确比较线段的长短还需要更加严谨的办法.
同学们，老师这里有一个问题：做手工时，在没有刻度尺的条件下，若想从较长的木棍上截下一段，使其等于短木棒，你有什么办法吗？
思考：在只有圆规和无刻度的直尺的情况下，大家想想办法，如何画出一条与已知线段相等的线段？提示：圆规可截取任意长度，相当于可以移动的“小木棍”.
结论：通过移动、对齐，可以在长木棒上“截取”相等长度的短木棒.
1.阅读课本164－166页，思考并回答以下问题：如图，已知线段a，画一条线段AB等于线段a.(请注意标上字母和结论)　
①用刻度尺画图，如图，AB就是所求作的线段．②根据课本164页示范，用圆规和无刻度的直尺画图，如图，AB就是所求作的线段．
2．线段的长短比较有两种方法：(用“＞”“＝”或“＜”填空)(1)叠合法：把其中一条线段移到另一条上作比较．如图①，AB____CD；如图②，AB____CD；如图③，AB___CD.(2)度量法：量出两条线段的长度进行比较．如图①，量出AB＝____cm，CD＝____cm，则AB___CD；如图②，量出AB＝____cm，CD＝____cm，则AB____CD；如图③，量出AB＝____cm，CD＝____cm，则AB____CD.
3．(1)两点的所有连线中，_____________．简单说成：____________________________．(2)连接两点的线段的长度，叫作这两点间的_________．
例1.如图，已知线段a、b，尺规作图：(1)画一条线段AC＝a＋b；(根据下列作法画出图形)作法：①用直尺画直线l；②用圆规在直线l上截取线段AB＝a(点B在点A的右侧)；③用圆规在直线l上截取线段BC＝b(点C在点B的右侧)；则线段AC即为所求．(2)画一条线段MN＝a－b；(3)画一条线段PQ＝2a－b.
例2.(1)如图，点C在线段AB上，AC＝8 cm，CB＝6 cm，点M、N分别是AC、BC的中点．求MN的长；(2)若C为线段AB上任意一点，满足AC＋CB＝a cm，点M、N分别是AC、BC的中点，请猜想MN的长．
(3)若C在线段AB的延长线上，且满足AC－CB＝b cm，点M、N分别是AC、BC的中点，请猜想MN的长，并画出图形，说明理由．
提疑惑：你有什么疑惑？
1．尺规作图：在数学中，我们常限定用无刻度的直尺和圆规作图，这就是尺规作图．2．画一条线段等于已知线段：画法一(尺规作图)：如图所示，先用直尺画射线AC，再用圆规在射线AC上截取AB＝a.画法二(测量长度)：先量出线段a的长度，再画一条等于这个长度的线段．
知识点1：线段的画法及长短比较(重点)
3．线段的长短比较：(1)线段长短比较的实质是线段的长度的比较．(2)线段长短的比较方法：①度量法(数)：用刻度尺量出线段的长度，根据长度大小来比较，长度大的线段较长，长度相等时两线段相等．②叠合法(形)：比较两条线段AB与CD的长短，可以把线段AB移到线段CD上，使点A与点C重合，点B与点D在重合点的同一侧．
1．线段的基本事实：两点的所有连线中，线段最短．简单说成：两点之间，线段最短．2．两点间的距离：连接两点的线段的长度．
知识点2：线段的性质及两点间的距离(重点)
注：线段是一个图形，两点间的距离是指线段的长度，是一个数值，而不是线段本身，因此不能说“A，B两点间的距离是线段AB”，而应该说“A，B两点间的距离是线段AB的长度”．
知识点3：尺规作线段的和与差(难点)
用圆规在射线AE上截取线段AB＝a，再在射线BE上截取线段BC＝b
线段AC是线段a、b的和，即AC＝a＋b
用圆规在射线AE上截取线段AB＝a，再在线段AB上截取线段BD＝b
线段AD是线段a、b的差，即AD＝a－b
注：进行线段的和、差作图时，要掌握画一条线段等于已知线段的方法，作图时作图痕迹要保留，并且结论必须写明哪条线段是所求作的线段．
1．线段的中点：如图，点M在线段AB上，AM＝BM，点M叫作线段AB的中点. 应用：因为点M是线段AB的中点，所以AM＝BM＝ AB，AB＝2AM＝2BM.
知识点4：线段的中点及等分点(难点)
2．线段的等分点：如图①所示，B，C是线段AD上的两点，且AB＝BC＝CD＝ AD或AD＝3AB＝3BC＝3CD，我们称点B，C是线段AD的三等分点．类似地，还有线段的四等分点，如图②所示，AB＝BC＝CD＝DE＝ AE或AE＝4AB＝4BC＝4CD＝4DE.
【题型一】线段的长短比较
例1：如图，用圆规比较两条线段AB和A′B′的长短，结论正确的是(　 　)A．A′B′>AB B．A′B′＝ABC．A′B′变式：为比较线段AB、CD的长短，小明将点A与点C重合，使两条线段在一条直线上，点B在CD的延长线上，则(　 　)A．ABCD C．AB＝CD D．以上都有可能
例2：下列说法正确的是(　　)A．过A，B两点的直线的长度是A，B两点之间的距离B．线段AB就是A，B两点之间的距离C．在连接A，B两点的所有线中，最短线的长度是A，B两点之间的距离D．乘火车从上海到北京要行驶1 463千米，这就是说上海站与北京站之间的距离是1 463千米
【题型二】两点间的距离
变式：如图，C，D是线段AB上两点．若AC＝3，点C是线段AD的中点，AB＝10，则B，D两点之间的距离是____．
例3：下列四个现象中，可用“两点之间，线段最短”来解释的现象有(　 　)①用两个钉子就可以把木条固定在墙上；②植树时，只要确定两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能地沿着直线架设；④把弯曲的公路改直，就能缩短路程．A．①② B．①③ C．②④ D．③④
变式：如图，A，B是公路(直线l)两旁的两个村庄．若两个村庄要在公路上合修一个汽车站，使它到A，B两个村庄的距离之和最小，试在直线l上标出汽车站的位置，并说明作图依据．
解：如图，连接AB交直线l于点P，则点P即为汽车站的位置．依据：两点之间，线段最短．
例4：如图．(1)AD＝AB＋______＝AC＋_______＝______＋BC＋______；(2)AB＝AD－______＝AC－______＝______－BC－______；(3)AC＋BD－AD＝______．
【题型四】线段的和与差
例5：如图，已知线段a，b，求作线段AB＝2a－b.不写步骤，保留作图痕迹．
解：如图，线段AB即为所求作．
例6：点B在线段AC上，下列关系式：①AB＝ AC；②AB＝BC；③AC＝2BC；④AB＋BC＝AC.其中能表示点B是线段AC的中点的有(　　) A．1个 B．2个 C．3个 D．4个
【题型六】线段的中点及等分点