初中数学6 应用一元二次方程精品教学课件ppt

这是一份初中数学6 应用一元二次方程精品教学课件ppt，文件包含北师大版数学九年级上册261几何问题与行程问题课件pptx、261几何问题与行程问题-教学设计doc、261几何问题与行程问题-同步练习docx、261几何问题与行程问题-导学案doc等4份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

1）根据实际问题中的数量关系，正确列出一元二次方程。2）根据问题的实际意义，检验所得结果是否合理。3）通过一元二次方程解决实际生活问题。重点通过一元二次方程解决实际生活问题。难点通过实际问题中的数量关系，列方程并求解。
列方程解决实际问题的基本步骤：
1）审：分清已知未知，明确数量关系；
5）验：根据实际验结果；
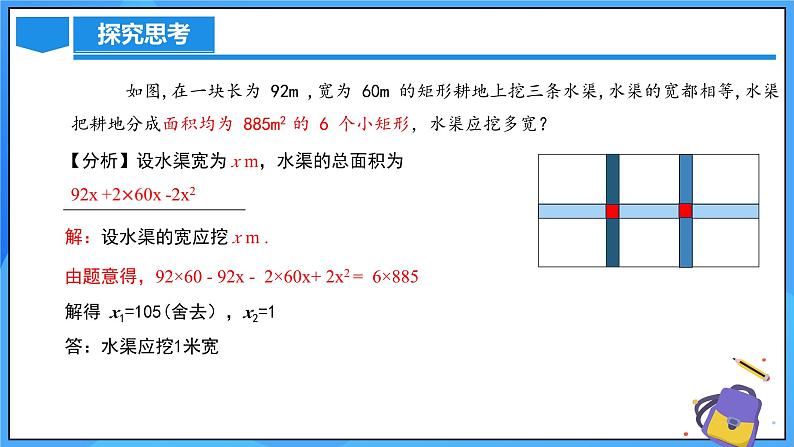
如图,在一块长为 92m ,宽为 60m 的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为 885m2 的 6 个小矩形，水渠应挖多宽？
【分析】设水渠宽为 x m，将所有耕地的面积拼在一起，变成一个新的矩形，它的长为 ___________m, 宽___________m.
解：设水渠的宽应挖 x m . ( 92 - 2x)（60 - x ）= 6×885
解得 x1=105(舍去），x2=1答：水渠应挖1米宽
【提问】尝试用其它方法求解？
【分析】设水渠宽为 x m，水渠的总面积为____________________
解：设水渠的宽应挖 x m .由题意得，92×60 - 92x - 2×60x+ 2x2 = 6×885
一块长和宽分别为60cm和40cm的长方形铁皮,要在它的四角截去四个相等的小正方形，折成一个无盖的长方体,使它的底面积为800cm2.求截去正方形的边长.
解:设截取正方形的边长为 x m,根据题意,得(60 - 2x)(40 - 2x) = 800. 整理得 x2 - 50x + 400 = 0. 解方程得x1=10 , x2= 40 (不合题意,舍去). 答:截取正方形的边长为10cm.
解：设x秒后，△ PCQ的面积是Rt △ABC面积的一半.根据题意整理，得x2 - 14x + 24 = 0.解方程，得 x1 = 2 , x2 = 12 (不符题意，舍去).答：2秒后，△ PCQ的面积是Rt △ABC面积的一半.
如图,在Rt△ABC中,∠C=90°，点P,Q同时由A,B两点出发,分别沿AC,BC方向向点C匀速移动（到点C为止），它们的速度都是1m/s.几秒后△PCQ的面积是Rt△ACB面积的一半?
如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动．几秒钟后△DPQ的面积等于28cm2？
【提示】设x s后△DPQ的面积等于28cm2，则AP、PB、BQ、QC的长度分别可用含x的代数式表示，从而Rt △DAP 、 Rt △PBQ、 Rt △QCD的面积也都可以用含x的代数式表示，于是可以列出方程。
几何问题与一元二次方程
常见几何图形周长或面积是等量关系.
例1 等腰梯形的面积为160cm2，上底比高多4cm，下底比上底多16cm，求这个梯形的高。
1．如图，在宽为20m，长为30m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为551m2，求道路的宽．
如图,某海军基地位于A处,在其正南方向200n mile处有一目标B,在B的正东方向200n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时D从出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.问题一：小岛D与小岛F相距多少海里?
解: 设相遇是补给船航行了x n mile,那么 DE = x n mile , AE + BE = 2x n mile, EF = AB + BF - (AB + BE) = (300 - 2x)n mile. 在Rt△DEF中，根据勾股定理可得方程 x2 = 1002 + (300 - 2x)2. 整理得： 3x2 - 1200x + 100000 = 0 , 解方程得 (不符题意舍去)
如图,某海军基地位于A处,在其正南方向200n mile处有一目标B,在B的正东方向200n mile处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时D从出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.问题二：已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)？
《九章算术》“勾股”章中有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何?”大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙的速度是3,乙一直向东走,甲先向南走 10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远?
解:设甲,乙相遇时所用时间为x,根据题意得(7x - 10)2 = (3x) 2 +10 2.整理得 2x2 - 7x = 0.解方程得 x1=3.5, x2=0 (不合题意,舍去).∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5.答:甲走了24.5步,乙走了10.5步.
【详解】解：设最快经过x小时，甲、乙两人相距6km，根据题意可得：BC＝（10﹣16x）km，DC＝12xkm，因为BC2+DC2＝BD2，则（10﹣16x）2+（12x）2＝62，解得：x1＝x2＝0.4．答：最快经过0.4小时，甲、乙两人相距6km．故选A．
2．一辆汽车以20m/s的速度行驶，司机发现前方路面有情况，紧急刹车后又滑行25m后停车．（1）从刹车到停车用了多少时间？（2）从刹车到停车平均每秒车速减少多少？（3）刹车后汽车滑行到15m时约用了多少时间（精确到0.1s）？
3．甲、乙两个机器人分别从相距70m的A、B两个位置同时相向运动．甲第1分钟走2m，以后每分钟比前1分钟多走1m，乙每分钟走5m．(1)甲、乙开始运动后多少分钟第一次同时到达同一位置？(2)如果甲、乙到达A或B后立即折返，甲继续每分钟比前1分钟多走1m，乙继续按照每分钟5m的速度行走，那么开始运动后多少分钟第二次同时到达同一位置？