重庆市两江巴蜀中学2023年数学八上期末检测试题【含解析】

这是一份重庆市两江巴蜀中学2023年数学八上期末检测试题【含解析】，共20页。试卷主要包含了考生必须保证答题卡的整洁，命题，下列因式分解结果正确的是等内容，欢迎下载使用。

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．满足下列条件的△ABC，不是直角三角形的为( )
A．∠A=∠B－∠CB．∠A∶∠B∶∠C=1∶1∶2C．b2=a2－c2D．a∶b∶c=2∶3∶4
2．如图，已知点A和直线MN，过点A用尺规作图画出直线MN的垂线，下列画法中错误的是（ ）
A．B．
C．D．
3．设(2a+3b)2＝(2a﹣3b)2+A，则A＝( )
A．6abB．12abC．0D．24ab
4．如图，在等边中，，将线段沿翻折，得到线段，连结交于点，连结、以下说法：①，②，③，④中，正确的有（ ）
A．个B．个C．个D．个
5．命题：①对顶角相等；②平面内垂直于同一条直线的两直线平行；③同位角相等④相等的角是对顶角；其中假命题有（ ）
A．1个B．2个C．3个D．4个
6．下列因式分解结果正确的是（ ）
A．2a2﹣4a=a（2a﹣4）B．
C．2x3y﹣3x2y2+x2y=x2y（2x﹣3y）D．x2+y2=（x+y）2
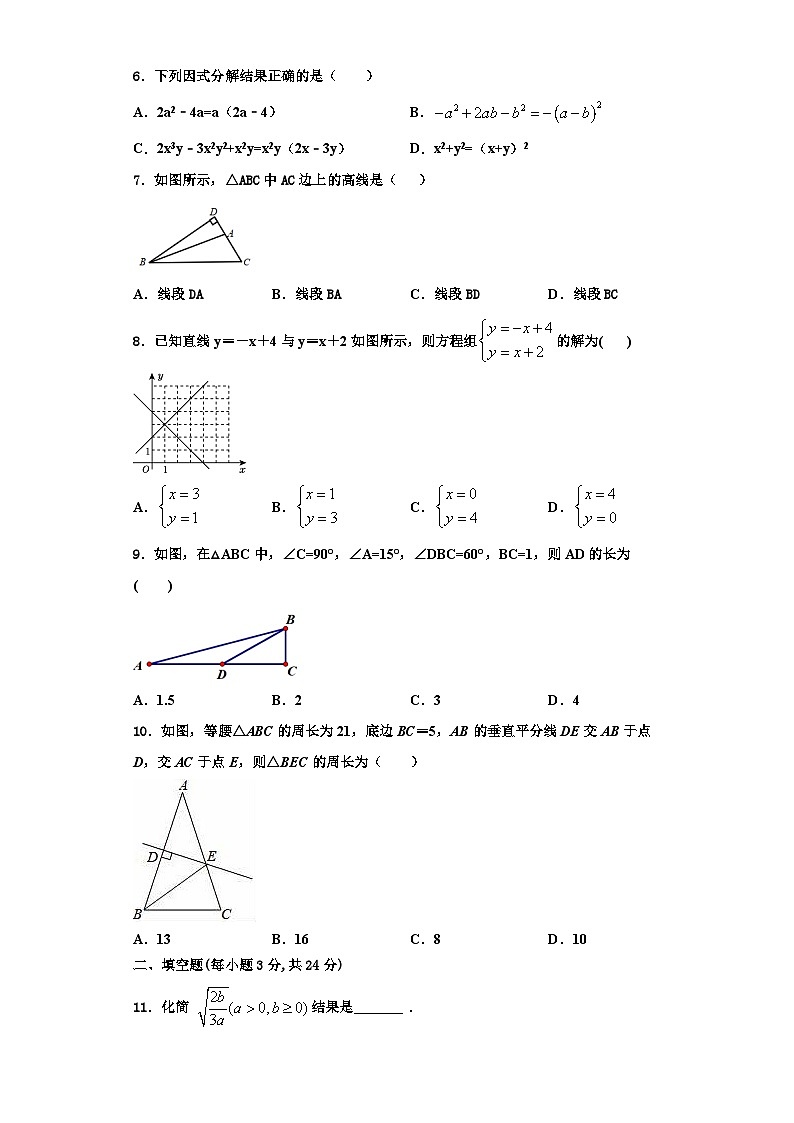
7．如图所示，△ABC中AC边上的高线是（ ）
A．线段DAB．线段BAC．线段BDD．线段BC
8．已知直线y＝－x＋4与y＝x＋2如图所示，则方程组的解为( )
A．B．C．D．
9．如图，在△ABC中，∠C=90°，∠A=15°，∠DBC=60°，BC=1，则AD的长为( )
A．1.5B．2C．3D．4
10．如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ）
A．13B．16C．8D．10
二、填空题(每小题3分,共24分)
11．化简 结果是_______ ．
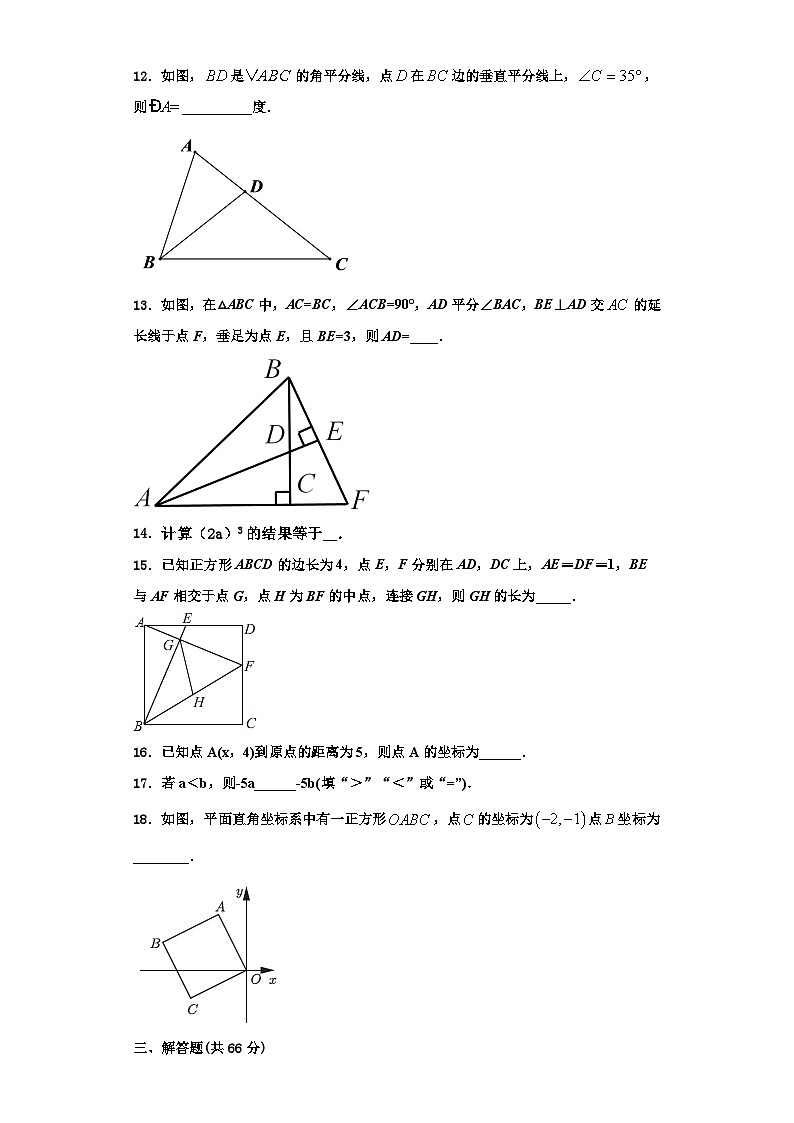
12．如图，是的角平分线，点在边的垂直平分线上，，则__________度．
13．如图，在△ABC中，AC=BC，∠ACB=90°，AD平分∠BAC，BE⊥AD交的延长线于点F，垂足为点E，且BE=3，则AD=____．
14．计算（2a）3的结果等于__．
15．已知正方形ABCD的边长为4，点E，F分别在AD，DC上，AE＝DF＝1，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为_____．
16．已知点A(x，4)到原点的距离为5，则点A的坐标为______．
17．若a＜b，则-5a______-5b(填“＞”“＜”或“=”)．
18．如图，平面直角坐标系中有一正方形，点的坐标为点坐标为________．
三、解答题(共66分)
19．（10分）小甘到文具超市去买文具．请你根据如图中的对话信息，求中性笔和笔记本的单价分别是多少元？
20．（6分）（尺规作图，保留作图痕迹，不写作法）如图，已知：△ABC（其中∠B＞∠A）．
（1）在边AC上作点D，使∠CDB＝2∠A；
（2）在（1）的情况下，连接BD，若CB＝CD，∠A＝35°，则∠C的度数为 ．
21．（6分）已知，如图所示，在中，．
（1）作的平分线交于点；
(要求：尺规作图，保留作图痕迹，不写作法．)
（2）若，，求的长．
22．（8分）如图，在平面直角坐标系中，点，；
(1)作关于轴的对称图形(点、、的对应点分别是、、)
(2)将向右平移2个单位长度，得到 (点、、的对应点分别是、、)
(3)请直接写出点的坐标．
23．（8分）如图，已知直线1经过点A（0，﹣1）与点P（2，3）．
（1）求直线1的表达式；
（2）若在y轴上有一点B，使△APB的面积为5，求点B的坐标．
24．（8分）（1）如图1，是的中线，，求的取值范围，我们可以延长到点，使，连接（如图2所示），这样就可以求出的取值范围，从而得解，请写出解题过程；
（2）在（1）问的启发下，解决下列问题：如图3，是的中线，交于点，交于点，且，求证：．
25．（10分）命题：如果三角形一边上的中线与这条边所对内角的平分线重合，那么这个三角形是等腰三角形．请自己画图，写出已知、求证，并对命题进行证明．
已知：如图，
求证：
证明：
26．（10分）解下列方程：
（1）
（2）
参考答案
一、选择题(每小题3分,共30分)
1、D
【解析】根据余角定理或勾股定理的逆定理即可判断.
【详解】A. ∠A=∠B－∠C得到∠B=90，故三角形是直角三角形；
B.设∠A=∠B=x，则∠C=2x，得x+x+2x=180，求得x=45，∴∠C=90，故三角形是直角三角形；
C.由b2=a2－c2得，故三角形是直角三角形；
D.设a=2x，则b=3x，c=4x，∵，∴此三角形不是直角三角形.
故选：D.
【点睛】
此题考查直角三角形的判定，可根据三个角的度数关系判断，也可根据三边的关系利用勾股定理的逆定理判定.
2、A
【分析】根据经过直线外一点作已知直线的方法即可判断．
【详解】解：已知点A和直线MN，过点A用尺规作图画出直线MN的垂线，
画法正确的是B、C、D选项，不符合题意．
A选项错误，符合题意；
故选：A．
【点睛】
本题考查了作图基本作图，解决本题的关键是掌握经过一点作已知直线的垂线的方法．
3、D
【解析】∵(2a+3b)2＝4a2+12ab+9b2, (2a-3b)2+A=4a2-12ab+9b2+A, (2a+3b)2 =(2a-3b)2+A
∴4a2+12ab+9b2=4a2-12ab+9b2+A,
∴A=24ab;
故选D．
4、D
【分析】由△ABD≌△ACE，△ACE≌△ACM，△ABC是等边三角形可以对①②进行判断，由AC垂直平分EM和直角三角形的性质可对③进行判断，由△ADM是等边三角形可对④进行判断．
【详解】解：∵△ABC是等边三角形，
∴AB=AC，∠B=∠BAC=∠ACB=60°，
∵BD=CE，
∴△ABD≌△ACE（SAS）
∴AD=AE，∠BAD=∠CAE
∵线段沿翻折，
∴AE=AM，∠CAE=∠CAM，
∴，故①正确，
∴△ACE≌△ACM（SAS）
∴∠ACE=∠ACM=60°，故②正确，
由轴对称的性质可知，AC垂直平分EM，
∴∠CNE=∠CNM=90°，
∵∠ACM =60°，
∴∠CMN=30°，
∴在Rt△CMN中，，即，故③正确，
∵∠BAD=∠CAE，∠CAE=∠CAM，
∴∠BAD=∠CAM，
∵∠∠BAD+∠CAD=60°，
∴∠CAM +∠CAD=60°，
即∠DAM=60°，又AD=AM
∴△ADM为等边三角形，
∴故④正确，
所以正确的有4个，
故答案为：D．
【点睛】
本题考查了全等三角形的判定和性质、等边三角形的判定和性质、直角三角形的性质、线段垂直平分线的判定和性质、轴对称的性质等知识，解题的关键是灵活运用上述几何知识进行推理论证．
5、B
【分析】利用对顶角的性质、平行线的性质分别进行判断后即可确定正确的选项．
【详解】①对顶角相等，正确，是真命题；
②在同一平面内，垂直于同一条直线的两直线平行，正确，是真命题；
③同位角相等，错误，是假命题；
④相等的角是对顶角，错误，是假命题，
故选：B．
【点睛】
本题考查了命题与定理的知识，解题的关键是了解对顶角的性质、平行线的性质等基础知识，难度较小．
6、B
【分析】根据因式分解的方法对各式进行判断即可得出答案．
【详解】A、2a2-4a=2a（a-2），故此选项错误；
B、-a2+2ab-b2=-（a-b）2，此选项正确；
C、2x3y-3x2y2+x2y=x2y（2x-3y+1），故此选项错误；
D、x2+y2无法分解因式，故此选项错误；
故选B．
【点睛】
此题主要考查了提取公因式法以及公式法分解因式，熟练掌握乘法公式是解题关键．
7、C
【解析】从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高.
【详解】由图可知，中AC边上的高线是BD.
故选：C.
【点睛】
掌握垂线的定义是解题的关键.
8、B
【解析】二元一次方程组的解就是组成二元一次方程组的两个方程的公共解，即两条直线y＝－x＋4与y＝x＋2的交点坐标．
故选B
点睛：本题考查了一次函数与二元一次方程组．二元一次方程组的解就是组成该方程组的两条直线的图象的交点．
9、B
【分析】先利用∠C=90°，∠DBC=60°，求出∠BDC=30°，再利用30°所对的直角边是斜边的一半可求出BD的长，再利用外角求出∠DBA，即可发现AD=BD.
【详解】解：∵∠C=90°，∠DBC=60°
∴∠BDC=30°
∴BD=2BC=2
又∵∠BDC是△BDA的外角
∴∠BDC=∠A＋∠DBA
∴∠DBA=∠BDC－∠A=15°
∴∠DBA=∠A
∴AD=BD=2
故选B
【点睛】
此题考查的是（1）30°所对的直角边是斜边的一半；（2）三角形的外角等于与它不相邻的两个内角之和；（3）等角对等边，解决此题的关键是利用以上性质找到图中各个边的数量关系
10、A
【分析】由于△ABC是等腰三角形，底边BC＝5，周长为21，由此求出AC＝AB＝8，又DE是AB的垂直平分线，根据线段的垂直平分线的性质得到AE＝BE，由此得到△BEC的周长＝BE+CE+CB＝AE+CE+BC＝AC+CB，然后利用已知条件即可求出结果．
【详解】解：∵△ABC是等腰三角形，底边BC＝5，周长为21，
∴AC＝AB＝8，
又∵DE是AB的垂直平分线，
∴AE＝BE，
∴△BEC的周长＝BE+CE+CB＝AE+CE+BC＝AC+CB＝1，
∴△BEC的周长为1．
故选A．
【点睛】
此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．
二、填空题(每小题3分,共24分)
11、
【分析】首先将被开方数的分子和分母同时乘以3a，然后再依据二次根式的性质化简即可．
【详解】解：原式=，
故答案为：．
【点睛】
本题主要考查的是二次根式的性质与化简，熟练掌握相关知识是解题的关键．
12、1
【分析】由线段垂直平分线的性质可得DB=DC，根据等腰三角形的性质可得∠DBC的度数，根据角平分线的性质可得∠ABD的度数，再根据三角形的内角和即得答案．
【详解】解：∵点在边的垂直平分线上，∴DB=DC，∴∠DBC=，
∵是的角平分线，∴∠ABD=，
∴．
故答案为：1．
【点睛】
本题考查了线段垂直平分线的性质、等腰三角形的性质、角平分线的定义和三角形的内角和定理等知识，属于基础题型，熟练掌握上述基本知识是解题关键．
13、1
【分析】由题意易证△ACD≌△BCF，△BAE≌△FAE，然后根据三角形全等的性质及题意可求解．
【详解】解： AD平分∠BAC，BE⊥AD，
∠BAE=∠FAE，∠BEA=∠FEA=90°，
AE=AE，
△BAE≌△FAE，
BE=EF，
BE=3，
BF=1，
∠ACB=90°，∠F+∠FBC=90°，∠EAF+∠F=90°，
∠ACD=∠BCF=90°，∠FBC=∠DAC，
AC=BC，
△ACD≌△BCF，
AD=BF=1；
故答案为1．
【点睛】
本题主要考查全等三角形的性质与判定，熟练掌握三角形全等判定的条件是解题的关键．
14、8
【解析】试题分析：根据幂的乘方与积的乘方运算法则进行计算即可
考点：(1)、幂的乘方；(2)、积的乘方
15、．
【分析】利用正方形的性质证出△ABE≌△DAF，所以∠ABE＝∠DAF，进而证得△GBF是直角三角形，利用直角三角形斜边中线等于斜边一半可知GH＝BF，最后利用勾股定理即可解决问题.
【详解】解：∵四边形ABCD为正方形，
∴∠BAE＝∠D＝90°，AB＝AD，
在△ABE和△DAF中，
∵ ，
∴△ABE≌△DAF（SAS），
∴∠ABE＝∠DAF，
∵∠ABE+∠BEA＝90°，
∴∠DAF+∠BEA＝90°，
∴∠AGE＝∠BGF＝90°，
∵点H为BF的中点，
∴GH＝BF，
∵BC＝4、CF＝CD﹣DF＝4﹣1＝3，
∴BF＝＝5，
∴GH＝BF＝，
故答案为：．
【点睛】
本题考点涉及正方形的性质、三角形全等的证明、直角三角形斜边中线定理、勾股定理等知识点，难度适中，熟练掌握相关性质定理是解题关键.
16、 (1，4)或(-1，4)
【分析】根据两点间的距离公式便可直接解答．
【详解】解：∵点A（x，4）到原点的距离是5，点到x轴的距离是4，
∴5=，解得x=1或x=-1．
A的坐标为（1，4）或（-1，4）．
故答案填：（1，4）或（-1，4）．
【点睛】
本题考查了勾股定理以及点的坐标的几何意义，解题的关键是明确横坐标的绝对值就是点到y轴的距离，纵坐标的绝对值就是到x轴的距离．
17、＞
【解析】试题解析：∵a＜b，
∴-5a＞-5b；
18、
【分析】过点作轴于，过点作轴，过点作交CE的延长线于．先证明，得到，，根据点的坐标定义即可求解．
【详解】解：如图，过点作轴于，过点作轴，过点作交CE的延长线于．
，
，．
四边形是正方形，
．
易求．
又
∴，
，，
点的坐标为，，
点到轴的距离为，
点的坐标为．
故答案为：
【点睛】
本题考查了平面直角坐标系点的坐标，全等三角形的判定与性质，根据题意，添加辅助线构造全等三角形是解题关键．
三、解答题(共66分)
19、2元、6元
【解析】根据对话分别利用总钱数得出等式求出答案．
【详解】解：设中性笔和笔记本的单价分别是元、元，根据题意可得：
，
解得：，
答：中性笔和笔记本的单价分别是2元、6元．
【点睛】
此题主要考查了二元一次方程组的应用，正确得出等量关系是解题关键．
20、 (1)见解析；（2）40°．
【分析】（1）作线段AB的中垂线，与AC的交点即为所求点D；
（2）由CB=CD知∠CDB=2∠A=70°，再由CD=CB知∠CDB=∠CBD=70°，根据三角形的内角和定理可得答案．
【详解】解：（1）如图所示，点D即为所求．
（2）∵CB＝CD，
∴∠ABD＝∠A＝35°，
∴∠CDB＝2∠A＝70°，
又∵CD＝CB，
∴∠CDB＝∠CBD＝70°，
∴∠C＝40°，
故答案为40°．
【点睛】
本题主要考查作图-复杂作图，解题的关键是掌握线段中垂线的性质和尺规作图、等腰三角形的性质、三角形的内角和定理与外角的性质．
21、（1）答案见解析；（2）1
【解析】（1）根据角平分线的尺规作图步骤，画出图形即可；
（2）过点D作DE⊥AB于点E，先证明DE=DC=6，BC=BE，再根据AD=10，求出AE，设BC=x，则AB=x+8，根据勾股定理求出x的值即可．
【详解】（1）作图如下：
（2）过点D作DE⊥AB于点E，
∵DC⊥BC，BD平分∠ABC，
∴DE=DC=6，
∵AD=10，
∴AE=，
∵∠DBC=∠DBE，∠C=∠BED=90°，BD=BD，
∴∆DBC≅∆DBE（AAS），
∴BE=BC，
设BC=x，则AB=x+8，
∴在Rt△ABC中，由勾股定理得：x2+162=(x+8)2，
解得：x=12，
∴AB=12+8=1．
【点睛】
本题主要考查尺规作角平分线，角平分线的性质定理以及勾股定理，添加辅助线，构造直角三角形，利用勾股定理列方程，是解题的关键．
22、（1）详见解析；（2）详见解析；（3）．
【分析】（1）分别作出点、、关于x轴的对应点、、，再顺次连接即可；
（2）分别作出点、、向右平移2个单位后的对应点、、，再顺次连接即可；
（3）根据（2）题的结果直接写出即可．
【详解】解：（1）如图所示；
（2）如图所示；
（3）点的坐标是（1，﹣3）．
【点睛】
本题考查了坐标系中作已知图形的轴对称图形和平移变换作图，属于基本作图题型，熟练掌握作对称点的方法和平移的性质是解题的关键．
23、（1）y＝2x﹣1；（2）点B的坐标为（0，4）或（0，﹣6）．
【分析】（1）利用待定系数法求出直线l的表达式即可；
（2）设B（0，m），得出AB的长，由P的横坐标乘以AB长的一半表示出三角形APB面积，由已知面积列方程求出m的值，即可确定出B的坐标．
【详解】解：（1）设直线l表达式为y＝kx+b（k，b为常数且k≠0），
把A（0，﹣1），P（2，3）代入得：
，解得：，
则直线l表达式为y＝2x﹣1；
（2）设点B的坐标为（0，m），则AB＝|1+m|，
∵△APB的面积为5，
∴AB•xP＝5，即|1+m|×2＝5，
整理得：|1+m|＝5，即1+m＝5或1+m＝﹣5，
解得：m＝4或m＝﹣6，
故点B的坐标为（0，4）或（0，﹣6）．
【点睛】
本题是一次函数的综合题，涉及了待定系数法求一次函数解析式、三角形的面积等知识，解答本题的关键是数形结合思想及分类讨论思想的运用．
24、（1）；（2）见解析．
【分析】（1）延长到点，使，连接，易证，从而得，根据三角形三边关系，可得，进而即可求解；
（2）先证，结合，可得，结合，即可得到结论．
【详解】（1），
（SAS），
∴，
∴在中， ，
即：，
∴的范围是：；
（2）延长到点，使，连接，
由（1）知：，
，
，
，
，
，
，
．
【点睛】
本题主要考查三角形全等的判定和性质定理，三角形三边的关系，等腰三角形的性质和判定定理，添加辅助线，构造全等三角形，是解题的关键．
25、见解析
【分析】由角平分线的性质得出DE=DF，证明Rt△BDE≌Rt△CDF（HL），得出∠B=∠C，即可得出结论．
【详解】已知：如图，在△ABC中，AD是BC边上的中线，AD平分∠BAC；
求证：AB=AC．
证明：作DE⊥AB于E，DF⊥AC于F，如图所示：
则∠BED=∠CFD=90°，
∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，
∴DE=DF，
∵AD是BC边上的中线，
∴BD=CD，
在Rt△BDE和Rt△CDF中，
，
∴Rt△BDE≌Rt△CDF（HL），
∴∠B=∠C，
∴AB=AC．
【点睛】
本题考查了等腰三角形的判定、全等三角形的判定与性质、角平分线的性质等知识；熟练掌握等腰三角形的判定定理，证明三角形全等是解题的关键．
26、（1）；（2）无解.
【分析】（1）方程两边同时乘以最简公分母x(x-3)，移项可得x的值，最后检验即可得答案；（2）方程两边同时乘以最简公分母(x-1)(x+2)，解方程即可求出x的值，检验即可得答案.
【详解】（1）最简公分母为
去分母
解得
检验：当时，.
∴原分式方程的解为
（2）最简公分母为
去分母
解得：
检验：当时，，
∴不是原分式方程的解.
∴原分式方程无解.
【点睛】
本题考查解分式方程，正确找出最简公分母是解题关键，注意解分式方程一定要检验是否有增根.