初中数学沪科版八年级上册14.2 三角形全等的判定课前预习ppt课件

这是一份初中数学沪科版八年级上册14.2 三角形全等的判定课前预习ppt课件，共19页。PPT课件主要包含了全等三角形的应用，求证∠B＝∠B等内容，欢迎下载使用。

1.能用两个三角形全等来证明平面图形中角相等，边相等.
2.知道全等三角形中对应的特殊线段(高、中线、角平分线)相等的性质.
3.知道全等三角形周长相等，面积相等.
◎重点:全等三角形的综合应用.
◎难点:全等三角形的特殊性质.
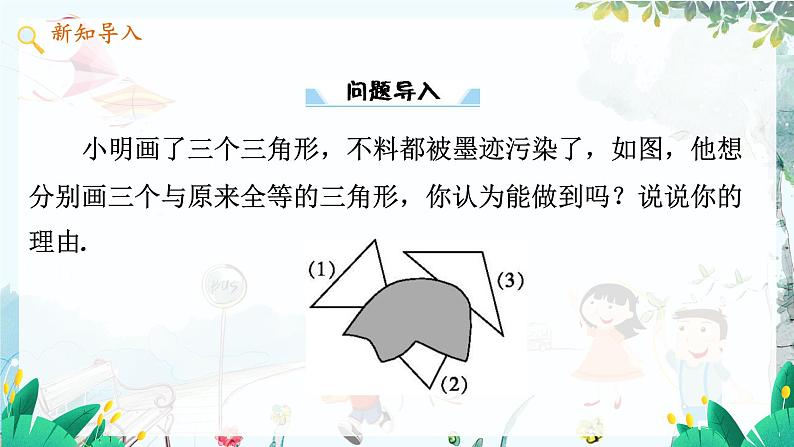
小明画了三个三角形，不料都被墨迹污染了，如图，他想分别画三个与原来全等的三角形，你认为能做到吗？说说你的理由.
全等三角形的综合应用 
阅读教材本课时，解决下列问题.
判定两个三角形全等的思路
全等三角形的特殊性质 
阅读课本“例9”的内容，解决下列问题.
揭示概念:全等三角形的对应边相等，对应角相等，面积　 相等 　，周长　相等　；全等三角形的对应边上的高　相等　，中线　相等　；全等三角形的对应角的角平分线　相等　. 
学法指导:两个三角形全等是指两个三角形能完全重合，那么它们的对应边上的中线、对应角的角平分线是不是一样能完全重合呢？我们也可以通过教材“例9”中的方法证明全等三角形对应边上的中线相等，对应角的角平分线相等.
1.如图，△ADC≌△EDC≌△EDB，则∠B的度数为(　B　)
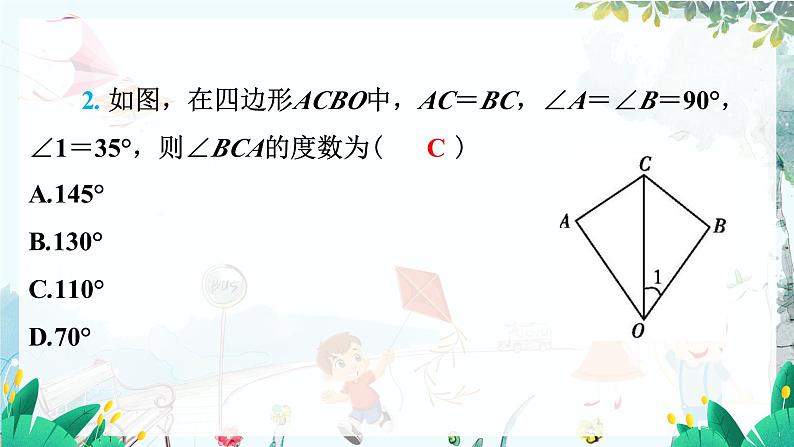
2. 如图，在四边形ACBO中，AC＝BC，∠A＝∠B＝90°，∠1＝35°，则∠BCA的度数为(　C　)
1. 如图，△ABC中，AB＝AC，点E在BC上，点D在AE上，有下列说法:①若E为BC中点，则有BD＝CD；②若BD＝CD，则E为BC中点；③若AE⊥BC，则有BD＝CD；④若BD＝CD，则AE⊥BC. 其中正确的有(　D　)
2.如图，在四边形ABCD中，AB＝AD，BC＝DC，E为AC上的一动点(不与A重合)，在点E移动过程中BE和DE是否相等？若相等，请写出证明过程；若不相等，请说明理由.
解:相等.理由如下:在△ABC和△ADC中，AB＝AD，AC＝AC，BC＝DC，∴△ABC≌△ADC(SSS)，∴∠DAE＝∠BAE，在△ADE和△ABE中，AB＝AD，∠DAE＝∠BAE，AE＝AE，∴△ADE≌△ABE(SAS)，∴BE＝DE.
3.证明:若两个锐角三角形的两边和其中一边上的高分别对应相等，则这两个三角形的第三边所对的角相等.
已知:如图，在△ABC和△A'B'C'中，AB＝A'B'，BC＝B'C'，AD、A'D'分别是BC、B'C'上的高，且AD＝A'D'.
证明:∵AD、A'D'分别是BC、B'C'上的高，∴∠ADB＝∠A'D'B'＝90°.在Rt△ABD和Rt△A'B'D'中，AB＝A'B'，AD＝A'D'，∴Rt△ABD≌Rt△A'B'D'(HL)，∴∠B＝∠B'.
【方法归纳交流】文字题的证明，先要根据题意将文字叙述转化为符号语言，画出图形，写出已知、求证，然后进行证明.
1.如图，在△ABE中，AB＝AE，AD＝AC，∠BAD＝∠EAC，BC、DE交于点O.求证:
(1)△ABC≌△AED；
(2)∠OBE＝∠OEB .
(2)由(1)可知∠ABC＝∠AED，∵AB＝AE，∴∠ABE＝∠AEB，∴∠ABE－∠ABC＝∠AEB－∠AED，即∠OBE＝∠OEB.
2.如图，已知AD∥BC，∠DAE＝∠BAE，∠ABE＝∠CBE，直线DC过点E交AD于点D，交BC于点C.求证:AD＋BC＝AB.
证明:在AB上截取AF＝AD，则有△ADE≌△AFE，∴∠D＝∠AFE，又AD∥BC，有∠D＋∠C＝180°，又∠AFE＋∠BFE＝180°，∴∠C＝∠BFE，