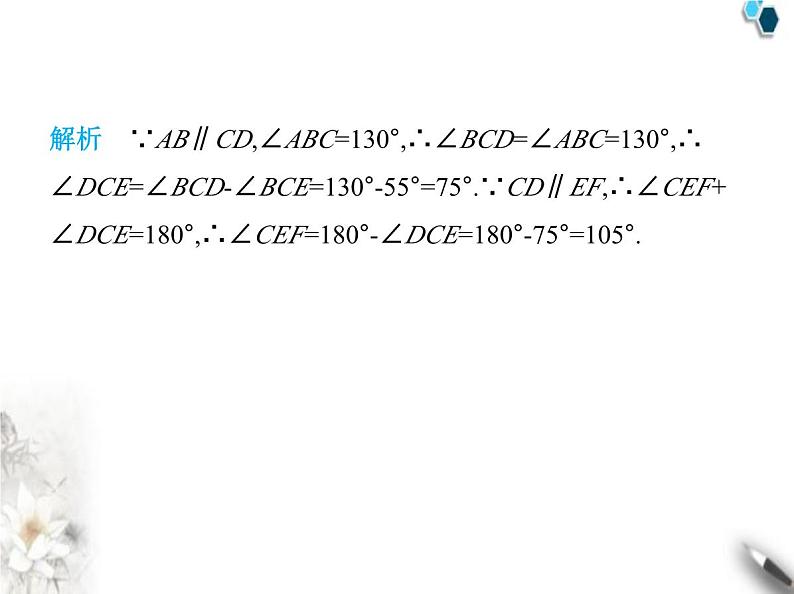
青岛版第5章 几何证明初步5.4 平行线的性质定理和判定定理课堂教学课件ppt

这是一份青岛版第5章 几何证明初步5.4 平行线的性质定理和判定定理课堂教学课件ppt，共28页。PPT课件主要包含了基础过关全练，能力提升全练，素养探究全练等内容，欢迎下载使用。

知识点1　平行线的性质定理
1.(2021山东聊城中考)如图,AB∥CD∥EF,若∠ABC=130°,∠ BCE=55°,则∠CEF的度数为 (　　)A.95°　    B.105°　    C.110°　    D.115°
解析　∵AB∥CD,∠ABC=130°,∴∠BCD=∠ABC=130°,∴ ∠DCE=∠BCD-∠BCE=130°-55°=75°.∵CD∥EF,∴∠CEF+ ∠DCE=180°,∴∠CEF=180°-∠DCE=180°-75°=105°.
2.(2023湖南益阳中考)如图,AB∥CD,直线MN与AB,CD分别 交于点E,F,CD上有一点G且GE=GF,∠1=122°,求∠2的度数.
解析　因为AB∥CD,所以∠MFD=∠1=122°,所以∠MFG=180°-∠MFD=180°-122°=58°.因为GE=GF,所以∠GFE=∠GEF=58°,所以∠2=180°-58°-58°=64°.
3.(2023湖北武汉中考)如图,在四边形ABCD中,AD∥BC,∠B= ∠D,点E在BA的延长线上,连接CE.(1)求证:∠E=∠ECD;(2)若∠E=60°,CE平分∠BCD,直接写出△BCE的形状.
解析　(1)证明:因为AD∥BC,所以∠EAD=∠B.因为∠B=∠D,所以∠EAD=∠D,所以BE∥CD,所以∠E=∠ECD.(2)△BCE是等边三角形,理由如下:因为CE平分∠BCD,所以∠BCE=∠ECD.因为EB∥CD,所以∠ECD=∠E=60°,所以∠B=180°-∠E-∠BCE=60°,所以∠B=∠BCE=∠E,所以△BCE是等边三角形.
知识点2　平行线的判定定理
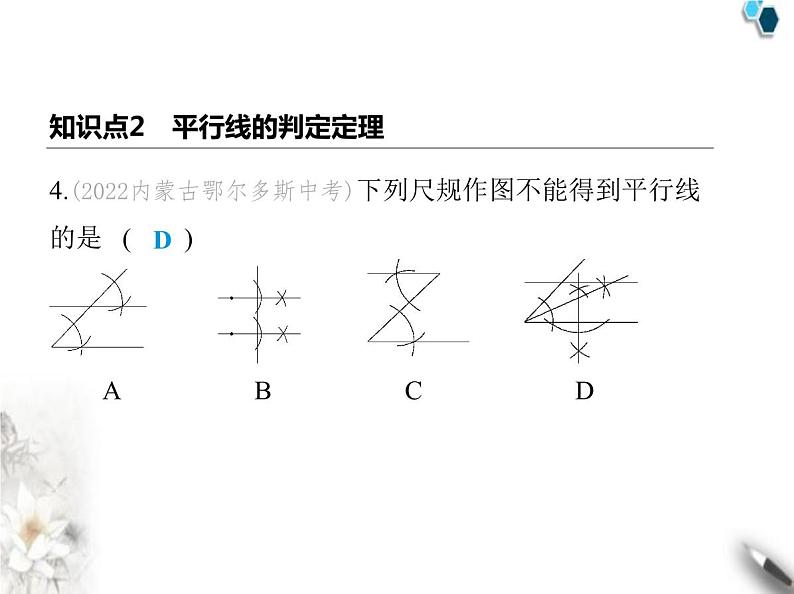
4.(2022内蒙古鄂尔多斯中考)下列尺规作图不能得到平行线 的是 (　　) A B C D
解析　通过尺规作一个角等于已知角,根据同位角相等,两直 线平行,选项A不符合题意;根据内错角相等,两直线平行,选 项C不符合题意;通过尺规作已知直线的垂线,根据在同一平 面内,垂直于同一直线的两直线平行,选项B不符合题意;通过 尺规作角平分线与一边的垂线,根据平行线的判定方法,选项 D不能保证两条直线平行,选项D符合题意.
5.(2024陕西咸阳秦都期末)如图,已知直线EF分别交直线AB, CD于点G,H,HM平分∠GHD交AB于点M,若∠BGE=50°,∠ GMH=25°,求证:AB∥CD.
证明　因为∠BGE=∠GMH+∠GHM,所以∠GHM=∠BGE-∠GMH=50°-25°=25°.
因为HM平分∠GHD,所以∠GHD=2∠GHM=50°,所以∠GHD=∠BGE,所以AB∥CD.
6.(2024河南新乡原阳期末)如图,BA平分∠CBD,且与线段CD 相交于点E,F是AC上一点,连接EF.若∠A=∠ABC,∠AFE+∠ CBD=180°.EF与BC平行吗?说明理由.
解析    EF与BC平行.理由如下:因为BA平分∠CBD,所以∠ABD=∠ABC.因为∠A=∠ABC,所以∠ABD=∠A,所以BD∥AC,所以∠ACB+∠CBD=180°.因为∠AFE+∠CBD=180°,所以∠ACB=∠AFE,所以EF∥BC.
知识点3　逆命题与逆定理
7.(2022上海中考)下列说法正确的是 (　　)A.命题一定有逆命题B.所有的定理一定有逆定理C.真命题的逆命题一定是真命题D.假命题的逆命题一定是假命题
解析　选项A,命题一定有逆命题,正确,符合题意;选项B,不 是所有的定理都有逆定理,例如全等三角形的对应角相等,没 有逆定理,原说法错误,不符合题意;选项C,真命题的逆命题 不一定是真命题,如“对顶角相等”的逆命题是假命题,原说 法错误,不符合题意;选项D,假命题的逆命题不一定是假命 题,例如假命题“角对应相等的两个三角形全等”,其逆命题 是真命题,原说法错误,不符合题意.
8.(一题多解)(2022湖北荆州中考,3,★☆☆)如图,直线l1∥l2, AB=AC,∠BAC=40°,则∠1+∠2的度数是     (　　)A.60°　    B.70°　    C.80°　    D.90°
解析　解法一:因为l1∥l2,所以∠1+∠ABC+∠BAC+∠2=180°.因为AB=AC,∠BAC=40°,所以∠ABC=∠ACB= =70°,所以∠1+70°+40°+∠2=180°,所以∠1+∠2=70°.故选B.解法二:过点C作CD∥l1,如图,因为l1∥l2,所以l1∥l2∥CD,所以∠1=∠BCD,∠2=∠ACD,
所以∠1+∠2=∠BCD+∠ACD=∠ACB.因为AB=AC,所以∠ACB=∠ABC,因为∠BAC=40°,所以∠ACB= (180°-∠BAC)=70°,所以∠1+∠2=70°.故选B.
9.(多选题)(2024山东潍坊昌乐期末,12,★★☆)如图,AB∥ CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥ EH于点G,且∠AFG=2∠D,则下列结论正确的是 (　　)A.∠D=30°
B.2∠D+∠EHC=90°C.FD平分∠HFBD.△FGH为等腰直角三角形
解析　因为FG⊥EH,所以∠EGF=∠FGH=90°.因为EH∥DF, 所以∠DFG=∠EGF=90°,所以∠AFG+∠DFB=180°-∠DFG =90°.因为AB∥CD,所以∠D=∠DFB,所以∠AFG+∠D=90°. 因为∠AFG=2∠D,所以∠D=30°,∠AFG=60°.因为EH∥DF, 所以∠D=∠EHC=30°,所以2∠D+∠EHC=90°,选项A,B都正 确;因为∠DFG=90°,∠HFD≠30°,所以∠HFD≠∠DFB,所以 FD不平分∠HFB,选项C不正确;因为∠DFG=90°,∠HFG≠45°,所以△FGH不是等腰直角三角形,选项D不正确.故选AB.
10.(2024北京师大附中期中,16,★★☆)如图,在Rt△ABC中, ∠C=90°,∠B=58°,点D,E分别在AB,AC上,将△ADE沿DE折叠 得到△FDE,且满足EF∥AB,则∠1=　　　    .
解析　在△ABC中,因为∠C=90°,∠B=58°,所以∠A=180°-(∠ C+∠B)=180°-(90°+58°)=32°.由折叠的性质,得∠1=∠FED. 因为EF∥AB,所以∠CEF=∠A=32°.因为∠CEF+∠FED+∠1 =180°,所以32°+2∠1=180°,解得∠1=74°.
11.(推理能力)(2024陕西汉中镇巴期末)【问题情境】已知∠ 1=∠2,EG平分∠AEC交BD于点G.【问题探究】(1)如图1,∠MAE=45°,∠FEG=15°,∠NCE=75°,试判断EF与 CD的位置关系,并说明理由;【问题解决】(2)如图2,∠MAE=140°,∠FEG=30°,当AB∥CD时,求∠NCE 的度数;
【问题拓展】(3)如图2,若AB∥CD,试说明∠NCE=∠MAE-2∠FEG.
解析　(1)EF∥CD.理由如下:因为∠1=∠2,所以AB∥EF,所以∠AEF=∠MAE=45°,所以∠AEG=∠AEF+∠FEG=60°.因为EG平分∠AEC,所以∠CEG=∠AEG=60°,所以∠CEF=∠CEG+∠FEG=75°.因为∠NCE=75°,
所以∠NCE=∠CEF,所以EF∥CD.(2)因为∠1=∠2,所以AB∥EF,所以∠MAE+∠FEA=180°,所以∠FEA=180°-∠MAE=40°.因为∠FEG=30°,所以∠AEG=∠FEA+∠FEG=70°.因为EG平分∠AEC,
所以∠CEG=∠AEG=70°,所以∠FEC=∠CEG+∠FEG=100°.因为AB∥CD,所以EF∥CD,所以∠NCE+∠FEC=180°,所以∠NCE=180°-∠FEC=80°.(3)证明:因为∠1=∠2,所以AB∥EF,所以∠MAE+∠FEA=180°,所以∠FEA=180°-∠MAE,
所以∠AEG=∠FEA+∠FEG=180°-∠MAE+∠FEG.因为EG平分∠AEC,所以∠GEC=∠AEG=180°-∠MAE+∠FEG,所以∠FEC=∠GEC+∠FEG=180°-∠MAE+∠FEG+∠FEG= 180°-∠MAE+2∠FEG.因为AB∥CD,AB∥EF,所以EF∥CD,所以∠FEC+∠NCE=180°,