初中数学北师大版七年级上册3.3 整式教案配套ppt课件

这是一份初中数学北师大版七年级上册3.3 整式教案配套ppt课件，共37页。PPT课件主要包含了典例讲练等内容，欢迎下载使用。
数学 七年级上册 BS版
1. 相关概念.（1）代数式：用运算符号把数和字母连接而成的式子叫作代数 式.单独一个 或一个 也是代数式.（2）单项式：由数与字母的 ⁠所组成的代数式叫作单项 式.一个单项式中，所有字母的指数和叫作这个单项式的次数.（3）多项式：几个单项式的 叫作多项式.一个多项式 中，单项式的个数叫作多项式的 ；次数最高的项 的 叫作这个多项式的次数.（4）整式： 和 统称为整式.
2. 求代数式的值的一般步骤.（1）代入：用具体的数值 代数式中对应的字母；（2）计算：按照代数式中给出的 计算出结果.
3. 整式加减运算.（1）同类项：所含字母 ，并且相同字母的指数也 ⁠ 的项叫作同类项.把同类项合并成一项叫作合并同类项.（2）去括号法则：括号前是“＋”号，把括号和它前面的 “＋”号去掉后，原括号里各项的符号都 ；括号前 是“－”号，把括号和它前面的“－”号去掉后，原括号里各 项的符号都要 ⁠.（3）整式的加减，实际上就是 和 ⁠.
4. 探索与表达规律.有两种形式：数字变化规律和图形变化规律.变化规律体现了由 特殊到一般的思想.
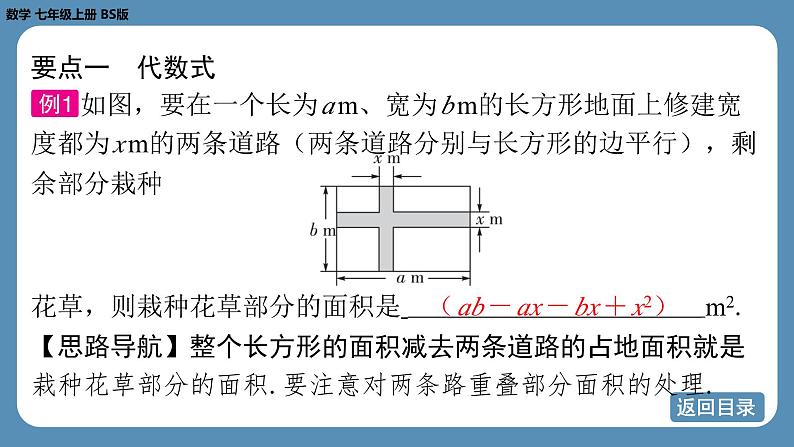
如图，要在一个长为 a m、宽为 b m的长方形地面上修建宽 度都为 x m的两条道路（两条道路分别与长方形的边平行），剩 余部分栽种
花草，则栽种花草部分的面积是 m2.【思路导航】整个长方形的面积减去两条道路的占地面积就是 栽种花草部分的面积.要注意对两条路重叠部分面积的处理.
（ ab － ax － bx ＋ x2）　
【解析】空白部分的面积＝大长方形的面积－两个阴影长方形 的面积＋两个阴影长方形重叠部分的面积，故栽种花草部分的 面积是（ ab － ax － bx ＋ x2）m2.故答案为（ ab － ax － bx ＋x2）.
【点拨】（1）用代数式表示图形的面积时，需掌握面积公式， 并能对图形作适当的分割或组合.（2）此题空白部分的面积也 可表示为（ a － x ）（ b － x ）.
2. 已知 a2＋2 a －5＝0，则代数式2 a2＋4 a －5的值是 ⁠.
已知整式（｜ k ｜－3） x3＋（ k －3） x2－ k .
（1）当 k 为何值时，该整式是单项式？
【思路导航】（1）根据单项式的定义得出关于 k 的方程，解答 即可；
解：（1）若关于 x 的整式是单项式，则有｜ k ｜－3＝0，且 k －3＝0，解得 k ＝3.故当 k 的值是3时，该整式是单项式.
（2）当 k 为何值时，该整式是二次多项式？
【思路导航】（2）若该整式为二次式，则三次项系数为0，据此得出关于 k 的方程，解答即可；
解：（2）若关于 x 的整式是二次多项式，则有｜ k ｜－3＝0，且 k －3≠0，解得 k ＝－3.故当 k 的值是－3时，该整式是二次多项式.
（3）当 k 为何值时，该整式是二项式？
【思路导航】（3）若该整式为二项式，需讨论是哪两项.
解：（3）因为关于 x 的整式是二项式，所以需分情况讨论：①当两项是二次项和常数项时，则有｜ k ｜－3＝0，且 k －3≠0， k ≠0，解得 k ＝－3；
②当两项是三次项和二次项时， k ＝0；
③当两项是三次项和常数项时，则有｜ k ｜－3≠0， k ≠0，且 k －3＝0，无解.综上所述，当 k 的值是－3或0时，该整式是二项式.
【点拨】几个单项式的和叫作多项式，每个单项式叫作多项式 的项，其中不含字母的项叫作常数项，单项式的个数叫作多项 式的项数.多项式中次数最高的项的次数叫作多项式的次数.
1. 下列说法中，正确的是（　D　）
先化简，再求值：
（1）－3 y2－6 y ＋2 y2＋5 y ，其中 y ＝2；
【思路导航】（1）先合并同类项，再代入值即可求解；
解：（1）原式＝－ y2－ y .当 y ＝2时，原式＝－22－2＝－4－2＝－6.
（2）15 a2－[－4 a2－（6 a － a2）－3 a ]，其中 a ＝－2；
【思路导航】（2）先去小括号，再去中括号，接着合并同类项，最后代入值即可求解；
解：（2）原式＝15 a2－（－4 a2－6 a ＋ a2－3 a ）＝15 a2－（－3 a2－9 a ）＝18 a2＋9 a .当 a ＝－2时，原式＝18×（－2）2＋9×（－2）＝54.
（3）3 xy ＋10 y ＋5 x －（2 xy ＋2 y －3 x ），其中 xy ＝2， x ＋ y ＝3.【思路导航】（3）先去括号，再合并同类项，最后把 xy 和 x ＋ y 的值代入即可求解.
解：（3）原式＝3 xy ＋10 y ＋5 x －2 xy －2 y ＋3 x ＝ xy ＋8 y ＋8 x ＝ xy ＋8（ x ＋ y ）.当 xy ＝2， x ＋ y ＝3时，原式＝2＋8×3＝26.
【点拨】解答整式的加减混合运算和求值的问题，关键是正确 去括号和合并同类项，注意整体思想的灵活运用.
1. 先化简，再求值：－2 y3＋（3 xy2－ x2 y ）－2（ xy2－ y3）， 其中｜2 x －2｜＋（ y ＋1）2＝0.
解：原式＝ xy2－ x2 y .因为｜2 x －2｜＋（ y ＋1）2＝0，所以2 x －2＝0， y ＋1＝0.
解得 x ＝1， y ＝－1.故原式＝1×（－1）2－12×（－1）＝2.
解：原式＝2 x3－3 x2 y －2 xy2－ x3＋2 xy2－ y3－ x3＋3 x2 y － y3＝ －2 y3.所以此题的结果与 x 的取值无关.当 y ＝－1时，原式＝－2×（－1）3＝2.
要点四　整式在实际生活中的应用
某公司在A，B两地分别有同型号的机器17台和15台，现要 从A，B两地将该机器运往甲地18台，乙地14台.已知运费如下 表：
若从A地运往甲地 x 台，则总运费需要多少元？（用含 x 的代数 式表示）【思路导航】总费用＝从A地运往甲地的费用＋从A地运往乙地 的费用＋从B地运往甲地的费用＋从B地运往乙地的费用，把相 关数值代入即可求解.
解：因为从A地运往甲地 x 台，A地有机器17台，所以从A地运往乙地（17－ x ）台.因为甲地需要18台，所以从B地运往甲地（18－ x ）台.因为乙地需要14台，所以从B地运往乙地14－（17－ x ）＝（ x －3）台.故总运费为600 x ＋500×（17－ x ）＋400×（18－ x ）＋800× （ x －3）＝（500 x ＋13300）元（3≤ x ≤17，且 x 为整数）.
【点拨】解决列代数式及相关计算问题，找到等量关系是解决 问题的关键.
某中学七（1）班5名老师决定带领本班 x 名学生去一景区旅游. 该景区每张门票的票价为40元，现有A，B两种购票方案可供选 择.方案A：教师全价，学生半价；方案B：不分教师与学生， 全部六折优惠.（1）请用含 x 的代数式分别表示选择A，B两种方案所需的 费用；
解：（1）方案A：40×5＋40×50％ x ＝（20 x ＋200）元；
方案B：40×60％（5＋ x ）＝（24 x ＋120）元.
（2）当学生人数 x ＝50时，且只选择其中一种方案购票，请通 过计算说明选择哪种方案更为优惠.
解：（2）当 x ＝50时，
方案A：20 x ＋200＝20×50＋200＝1200（元），
方案B：24 x ＋120＝24×50＋120＝1320（元）.因为1200＜1320，所以选择方案A更为优惠.
要点五　探索与表达规律
（1）一个三位数能否被3整除，只要看这个数的各数位上 的数字之和能否被3整除.你能说明其中的道理吗？
解：（1）设这个三位数为100 a ＋10 b ＋ c ，则100 a ＋10 b ＋ c ＝99 a ＋9 b ＋（ a ＋ b ＋ c ）＝9（11 a ＋ b ）＋（ a ＋ b ＋ c ），所以只要（ a ＋ b ＋ c ）能被3整除，9（11 a ＋ b ）＋（ a ＋ b ＋ c ）就能被3整除，即一个三位数能否被3整除，只要看这个数的各数位上的数字之 和能否被3整除.
（2）可以用（1）中的规律判断一个四位数能否被3整除吗？请 说明理由.【思路导航】先设每个数位上的数字，表示出三位数或四位 数，再变形看是否是3的倍数.
解：（2）可以用（1）中的规律判断一个四位数能否被3整除. 理由如下：设这个四位数是1000 a ＋100 b ＋10 c ＋ d ，则1000 a ＋100 b ＋10 c ＋ d ＝999 a ＋99 b ＋9 c ＋（ a ＋ b ＋ c ＋ d ）＝9（111 a ＋11 b ＋ c ）＋（ a ＋ b ＋ c ＋ d ），所以只要（ a ＋ b ＋ c ＋ d ）能被3整除，9（111 a ＋11 b ＋ c ）＋ （ a ＋ b ＋ c ＋ d ）就能被3整除.所以可以用（1）中的规律判断一个四位数能否被3整除.
【点拨】寻找规律并用字母表示这一规律体现了从特殊到一般 和归纳、猜想的数学思想的运用.解题中应注意先从特殊的结果 入手寻找规律，再用字母表示，最后加以验证.
……按照以上规律，解决下列问题：（1）写出第6个等式： ⁠；（2）请根据你的猜想写出第 n 个等式： （用含 n 的等式表示）.
2. 末两位是00，25，50，75的任何数均能被25整除，这是为什 么？请解释其中的道理.
解：设去掉末两位的数是 a .若末两位是00，则这个数可以表示为100 a .因为100 a 是25的倍数，所以末两位是00的任何数能被25整除；若末两位是25，则这个数可以表示为100 a ＋25.因为100 a ＋25＝25（4 a ＋1）是25的倍数，所以末两位是25的任何数能被25整除；
若末两位是50，则这个数可以表示为100 a ＋50.因为100 a ＋50＝25（4 a ＋2）是25的倍数，所以末两位是50的任何数能被25整除.同理可得，末两位是75的任何数能被25整除.故末两位是00，25，50，75的任何数均能被25整除.