






数学选择性必修第二册6.3空间向量的应用试讲课课件ppt
展开如何用向量表示空间当中的一个点P?
我们知道,空间中给定一个点A和一个方向就能唯一确定一条直线l,如何用向量表示空间中的直线l
类比问题1,取定空间中的任意一点O为基点,你能用向量表示直线l吗?
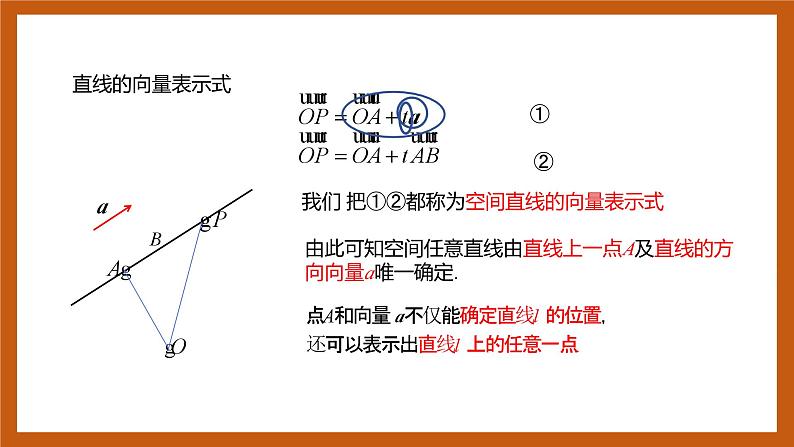
我们 把①②都称为空间直线的向量表示式
由此可知空间任意直线由直线上一点A及直线的方向向量a唯一确定.
基本事实1 过不在一条直线上的三个点,有且只有一个平面推论 1 经过一条直线和这条直线外一点,有且只有一个平面推论 2 经过两条相交直线,有且只有一个平面推论 3 经过两条平行直线,有且只有一个平面
怎样可以确定一个平面?
你能用向量表示这个平面吗?
一个定点和两个定方向能否确定一个平面?如果能,依据是什么?
同样的,类比刚刚的学习,我们取定空间中的任意一点O为基点,你能用向量表示平面吗?
我们把③称为空间平面ABC的向量表示式
可以看出,空间中任意平面由空间一点及两个不共线的向量唯一确定.
给定一个定点和一个定方向能否确定一个平面?
如果能,依据是什么?
过点A且垂直于直线l的平面是唯一确定的.
因此给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定.表示为集合 .
如果另有一条直线m⊥α ,在直线m上任取向量b,b与a有什么关系?
平面可由一点和任意一个法向量唯一确定.
1.已知向量a=(2,-1,3)和b=(-4,2x2,6x)都是直线l的方向向量,则x的值是A.-1 B.1或-1C.-3 D.1
解析 由题意得a∥b,
解析 ∵PA⊥平面ABCD,∴BD⊥PA.又AC⊥BD,∴BD⊥平面PAC,∴PC⊥BD.故选项B成立,选项A和D显然成立.故选C.
3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为A.(1,-1,1) B.(2,-1,1)C.(-2,1,1) D.(-1,1,1)
解析 显然a与b不平行,设平面α的法向量为n=(x,y,z),
令z=1,得x=-2,y=1.所以n=(-2,1,1).
4.已知向量 =(2,4,x),平面α的一个法向量n=(1,y,3),若AB⊂α,则A.x=6,y=2 B.x=2,y=6C.3x+4y+2=0 D.4x+3y+2=0
可得3x+4y+2=0.
5.已知A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的一个单位法向量是
解析 设平面ABC的法向量为n=(x,y,z),
∴x=y=z,又∵单位向量的模为1,故只有B正确.
6.已知平面α内有一个点A(2,-1,2),它的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是
7.(多选)如图,在正方体ABCD-A1B1C1D1中,E为棱CC1上不与C1,C重合的任一点,则能作为直线AA1的方向向量的是
解析 由定义知,一个向量对应的有向线段所在的直线与直线AA1平行或重合,则这个向量就称为直线AA1的一个方向向量.
8.在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:①直线CC1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).其中正确的是________.(填序号)
9.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,求平面EDB的一个法向量.
解 如图所示建立空间直角坐标系.
设平面EDB的法向量为n=(x,y,z),
取x=1,则y=-1,z=1,故平面EDB的一个法向量为n=(1,-1,1).
10.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,试建立恰当的空间直角坐标系,求平面PAB的一个法向量.
从而BD2+AD2=AB2,故BD⊥AD,以D为坐标原点,以射线DA,DB,DP为x,y,z轴的正半轴建立空间直角坐标系,
设平面PAB的一个法向量为n=(x,y,z).
11.(多选)已知直线l1的方向向量a=(2,4,x),直线l2的方向向量b=(2,y,2),若|a|=6,且a⊥b,则x+y的值是A.1 B.-1 C.3 D.-3
所以x=±4.因为a⊥b,所以a·b=2×2+4y+2x=0,
所以当x=4时,y=-3;当x=-4时,y=1.所以x+y=1或x+y=-3.
12.在三棱锥P-ABC中,CP,CA,CB两两垂直,AC=CB=1,PC=2,如图,建立空间直角坐标系,则下列向量是平面PAB的法向量的是
设平面PAB的一个法向量为n=(x,y,1),
所以n=(2,2,1).
13.已知直线l过点P(1,0,-1)且平行于向量a=(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是
高中数学湘教版(2019)选择性必修 第二册2.4 空间向量在立体几何中的应用试讲课ppt课件: 这是一份高中数学湘教版(2019)选择性必修 第二册<a href="/sx/tb_c4018232_t3/?tag_id=26" target="_blank">2.4 空间向量在立体几何中的应用试讲课ppt课件</a>,共1页。
高中数学北师大版 (2019)选择性必修 第一册4. 1 直线的方向向量与平面的法向量获奖ppt课件: 这是一份高中数学北师大版 (2019)选择性必修 第一册<a href="/sx/tb_c4017381_t3/?tag_id=26" target="_blank">4. 1 直线的方向向量与平面的法向量获奖ppt课件</a>,共24页。PPT课件主要包含了共线向量定理,共面向量定理,问t0时,平面的法向量,平面α的向量式方程,-1-11等内容,欢迎下载使用。
湘教版(2019)选择性必修 第二册2.4 空间向量在立体几何中的应用图片ppt课件: 这是一份湘教版(2019)选择性必修 第二册2.4 空间向量在立体几何中的应用图片ppt课件,共20页。PPT课件主要包含了直线的方向向量,平面的法向量,判断正误,即时巩固,∴y-z=0,求平面的法向量,∵x∈0π等内容,欢迎下载使用。













