2024年小升初数学暑假专题训练 专题1 圆柱与圆锥（北师大版）

这是一份2024年小升初数学暑假专题训练 专题1 圆柱与圆锥（北师大版），文件包含2024年小升初数学暑假专题训练专题1圆柱与圆锥教师版北师大版docx、2024年小升初数学暑假专题训练专题1圆柱与圆锥学生版北师大版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。


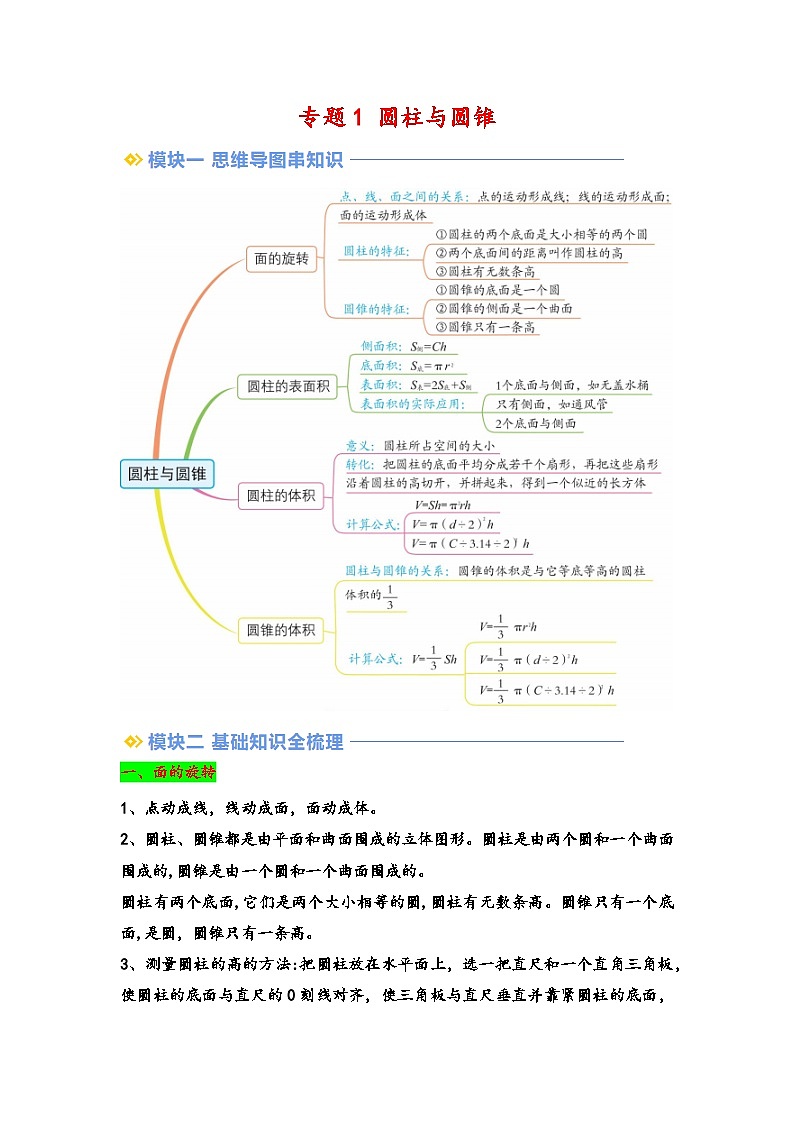
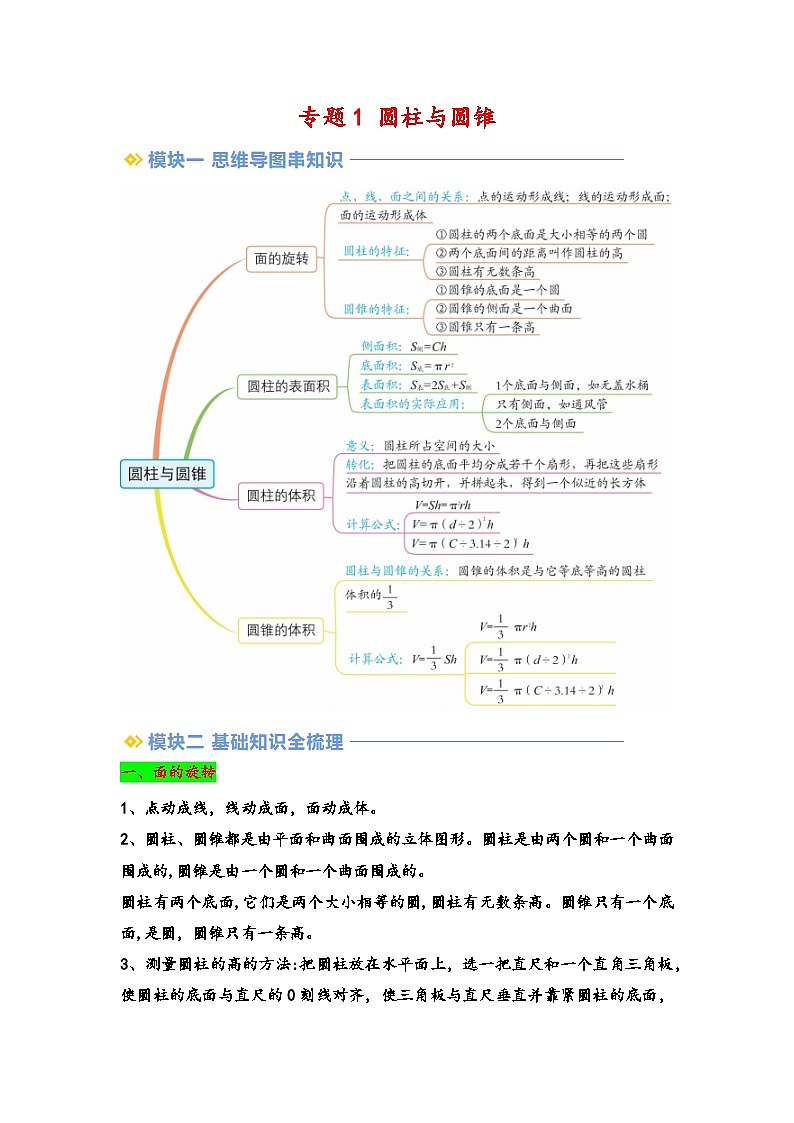
一、面的旋转
1、点动成线，线动成面，面动成体。
2、圆柱、圆锥都是由平面和曲面围成的立体图形。圆柱是由两个圆和一个曲面围成的,圆锥是由一个圆和一个曲面围成的。
圆柱有两个底面,它们是两个大小相等的圆,圆柱有无数条高。圆锥只有一个底面,是圆，圆锥只有一条高。
3、测量圆柱的高的方法:把圆柱放在水平面上，选一把直尺和一个直角三角板，使圆柱的底面与直尺的0刻线对齐，使三角板与直尺垂直并靠紧圆柱的底面，此时圆柱的另一个底面对准的刻度值即是圆柱的高。
4、测量圆锥的高的方法:把圆锥放在水平面上，在圆锥的顶点上放一个平面的东西，比如一块木板，并与底面平行，测量一下这两个平面间的距离，这两个平面间的距离就是圆锥的高。
二、圆柱的表面积
1、圆柱的侧面积。
圆柱的侧面如果沿高剪开得到一个长方形。
长方形的长就是圆柱的底面的周长，长方形的宽就是圆柱的高。
圆柱的侧面积=底面周长×高，用字母表示:S侧=Ch
2、圆柱的表面积。
圆柱的表面积=侧面积+两个底面积
圆柱的表面积公式：S表=2πr²+2πrh。
圆柱的表面积=侧面积+两个底面积（S表=S侧+2S底）；
圆柱的底面积=圆的面积，也就是S底=πr²。
三、圆柱的体积
1、意义：圆柱形物体所占空间的大小叫作圆柱的体积。
2、圆柱的体积的计算公式。
把一个圆柱的底面平均分成若干个相等的扇形，再把这些扇形按照等分线沿高剪开，等分成若干份，就可以拼成一个近似的长方体。
长方体的体积= 长 × 宽×高
↓ ↓ ↓ ↓
圆柱的体积=底面周长的一半×半径底面积×高
用字母表示：V=S×h
V=πr2×h
3、不规则物体的体积。
计算不规则物体的体积，可以借助圆柱形容器和水，给圆柱形容器里装适量的水，量出水的高度，把不规则物体放入容器完全浸入水中，并且水不被溢出，这时测量水的高度，上升的水的体积就是不规则物体的体积。
四、圆锥的体积
1、意义：圆锥形物体所占空间的大小叫作圆锥的体积。
2、圆锥的体积公式。
一个圆锥和一个圆柱的底面积和高都相等，将圆锥形容器装满沙子，再倒入圆柱形容器，3次可以倒满。所以说圆锥的体积等于与它等底等高的圆柱体积的13。
圆锥的体积=圆柱的体积×13
用字母表示为V=13Shπr2h×13

一．选择题
1．（2024春•伊通县期中）一个饮料瓶（如图所示），容积是。瓶子里饮料的高度是，将这个饮料瓶盖子拧紧倒置放平，空余部分的高度是。这个饮料瓶的底面积是 。
A．120B．0.12C．12D．1.2
2．（2024•淮滨县模拟）乐乐把一个圆柱展开，得到一个长方形和两个圆，如图（单位：，这个圆柱的高是 。
A．18.84B．9.42C．12.56D．16
3．（2024春•云浮期中）如果圆锥的底面半径扩大到原来的2倍，高缩小到原来的，则体积是原来的
A．2倍B．1倍C．D．
4．（2024春•瑞安市期中）有一张长，宽的长方形纸片，聪聪沿着长卷一圈刚好围成圆柱的侧面，明明沿着宽卷一圈，也刚好围成圆柱的侧面，比较两个圆柱的侧面积和体积，
A．侧面积和体积都相同。B．侧面积和体积都不相同。
C．侧面积不同，体积相同。D．侧面积相同，体积不同。
5．（2024春•鹿城区期中）甲、乙两个圆锥的高之比是，直径之比是，那么甲、乙两个圆锥的体积之比是
A．B．C．D．
6．（2024春•西安期中）一个底面半径是的圆锥，它的高如果增加，它的体积将会增加 。
A．339.12B．113.04C．37.68D．12.56
二．填空题
7．（2024春•鹿城区期中）在一个棱长是4分米的正方体木料中，削出一个最大的圆柱。这个圆柱的体积是 立方分米，这根木料的利用率是 。
8．（2024春•商水县期中）在一个棱长是的正方体水箱中盛满水，再将水全部倒入一个底面积是，高是的圆柱形水桶中，水深 。
9．（2024春•商水县期中）一个底面积是的圆柱形水桶中装有水，水中放一个底面半径为，高为的圆锥，且完全浸没在水中。如果把圆锥从水桶中取出来，水面会下降 。
10．（2024•永寿县模拟）一个圆柱形水桶，从里面量底面半径是10厘米，高是40厘米，里面水深30厘米，把一个底面半径是5厘米的圆锥形铁块完全浸没在水中，这时水面上升1厘米。这个圆锥形铁块的体积是 立方厘米，高是 厘米。
11．（2024春•迁安市期中）一根长2米的圆柱形木料，把它锯成两个小圆柱后，表面积比原来增加了12.56平方分米。这根木料原来的体积是 立方分米。
12．（2024春•蚌埠期中）如图，将一个圆锥沿底面直径和高切分成完全相同的两部分，表面积比原来多了60平方分米，圆锥的高是5分米，圆锥的体积是 立方分米，比和它等底等高的圆柱体积少 立方厘米。
三．判断题
13．（2024春•凤翔区期中）一枚硬币厚2毫米，将10枚这样的硬币摞成一个圆柱，这个圆柱的高是20厘米。
14．（2024春•礼泉县期中）旋转后会得到一个圆台。
15．（2024春•邢台期中）一个圆柱的底面直径是5厘米，若高减少2厘米，则侧面积减少了62.8平方厘米。
16．（2024春•广平县期中）把一个圆柱削成最大的圆锥后体积减少了36立方厘米，这个圆锥的体积是18立方厘米。
四．计算题
17．（2024春•富平县期中）求下面图形的体积。
（1）（2）
18．（2024春•灌云县期中）计算如图立体图形的体积。
五．操作题
19．（2024春•仁寿县期中）一个圆柱的侧面积是，高是，请在如图的方格纸上画出这个圆柱的两个底面。（每个小方格的面积表示
六．解答题
20．（2024春•邵阳期中）元代的一种圆形钱币（如图）直径约为8厘米，厚度为4毫米，正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来，求垒起来的钱币的体积大约是多少立方厘米。
21．（2024春•临汾期中）在一个底面半径是10厘米的圆柱形状的容器中装着一些水，水里放了一个底面直径10厘米的圆锥形状的铅锤，当铅锤从容器中取出后，容器中水面下降5毫米，铅锤的高是多少厘米？
22．（2024•怀化模拟）一个圆柱形木桶的底面内直径为，组成木桶的木板长短不一，高度分别有、、。
（1）如果将这个水桶水平放置，盛满水（如图一），那么水的体积是多少升？
（2）如果将木桶倾斜（如图二），重新加水，使水在木桶中呈现图三的形状，这时水的体积又是多少升？
23．（2022•靖边县）沙漏又称沙钟，是我国古代一种计量时间的仪器，它是根据沙从一个容器到另一个容器的数量来计算时间，如图展示了一个沙漏记录时间的情况。
（1）求出沙漏此时上部分的体积。
（2）如果再过1分，沙漏上部的沙子就可以全部被漏到下部，那么现在已经计量了多少分钟？
24．（2023•无棣县）一个平面图形经过平移或旋转可以形成立体图形。例如，分别将长方形、圆作为底面，向上平移可以得到长方体、圆柱（如图，它们的体积均可以用“底面积高”进行计算；将一个长4厘米，宽3厘米的长方形，绕着长旋转一周，可以得到一个圆柱（如图。
（1）将一个底面直径 厘米的圆作为底面，向上平移 厘米，也可以形成图2中的圆柱。
（2）将一个两条直角边均为4厘米的直角三角作为底面，向上平移5厘米，形成一个立体图形（如图，它体积是多少立方厘米？
25．（2023秋•松北区期末）已知冰融化成水后，体积会减少。现有一块立方厘米的冰，经过一段时间后，全部融化成水。
（1）这块冰融化成水后，水的体积是多少立方厘米？
（2）一张长方形铁皮如图1所示，把图中阴影部分剪下，刚好做成一个带盖的圆柱形铁桶（接缝忽略不计），底面圆的直径为8厘米。现在将（1）的水全部倒入这个带盖的圆柱形铁桶（如图中，求此时水面的高度与圆柱形铁桶高度的比值；
（3）如图3，在（2）的条件下，把一个底面半径为1厘米的圆柱体铁块垂直放入圆柱形铁桶中，当它的一个底面在水中与圆柱形铁桶底面完全接触时仍有露出水面。如果再把这个圆柱体的铁块熔成一个与之等底面积圆锥体铁块，求这个圆锥体铁块的高度。