高考数学大一轮复习精讲精练(新高考地区)2.4幂函数和二次函数(精讲)(原卷版+解析)

这是一份高考数学大一轮复习精讲精练(新高考地区)2.4幂函数和二次函数(精讲)(原卷版+解析)，共17页。


【知识储备】
1．幂函数
(1)幂函数的定义
一般地，函数y＝xα叫做幂函数，其中x是自变量，α为常数．
(2)常见的五种幂函数的图象
(3)幂函数的性质
①幂函数在(0，＋∞)上都有定义；
②当α>0时，幂函数的图象都过点(1,1)和(0,0)，且在(0，＋∞)上单调递增；
③当α<0时，幂函数的图象都过点(1,1)，且在(0，＋∞)上单调递减；
④当α为奇数时，y＝xα为奇函数；当α为偶数时，y＝xα为偶函数．
2．二次函数
(1)二次函数解析式的三种形式
一般式：f(x)＝ax2＋bx＋c(a≠0)．
顶点式：f(x)＝a(x－m)2＋n(a≠0)，顶点坐标为(m，n)．
零点式：f(x)＝a(x－x1)(x－x2)(a≠0)，x1，x2为f(x)的零点．
(2)二次函数的图象和性质
【题型精讲】
【题型一 幂函数的图像与性质】
例1 (2023·江西高三月考）已知函数是幂函数，直线过点，则的取值范围是（ ）
A．B．C．D．
例2 (2023·全国·高三测试）图中C1、C2、C3为三个幂函数在第一象限内的图象，则解析式中指数的值依次可以是（ ）
A．、、B．、、C．、、D．、、
例3 (2023·黑龙江·哈九中高三开学考试）已知幂函数的图象过点，且，则a的取值范围是______．
例4 (2023·北京人大附中高三月考）设则“的图象经过”是“为奇函数”的（ ）
A．充分不必要件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【题型精练】
1. (2023·河北·邢台市第二中学高三开学考试）幂函数在上单调递增，则______．
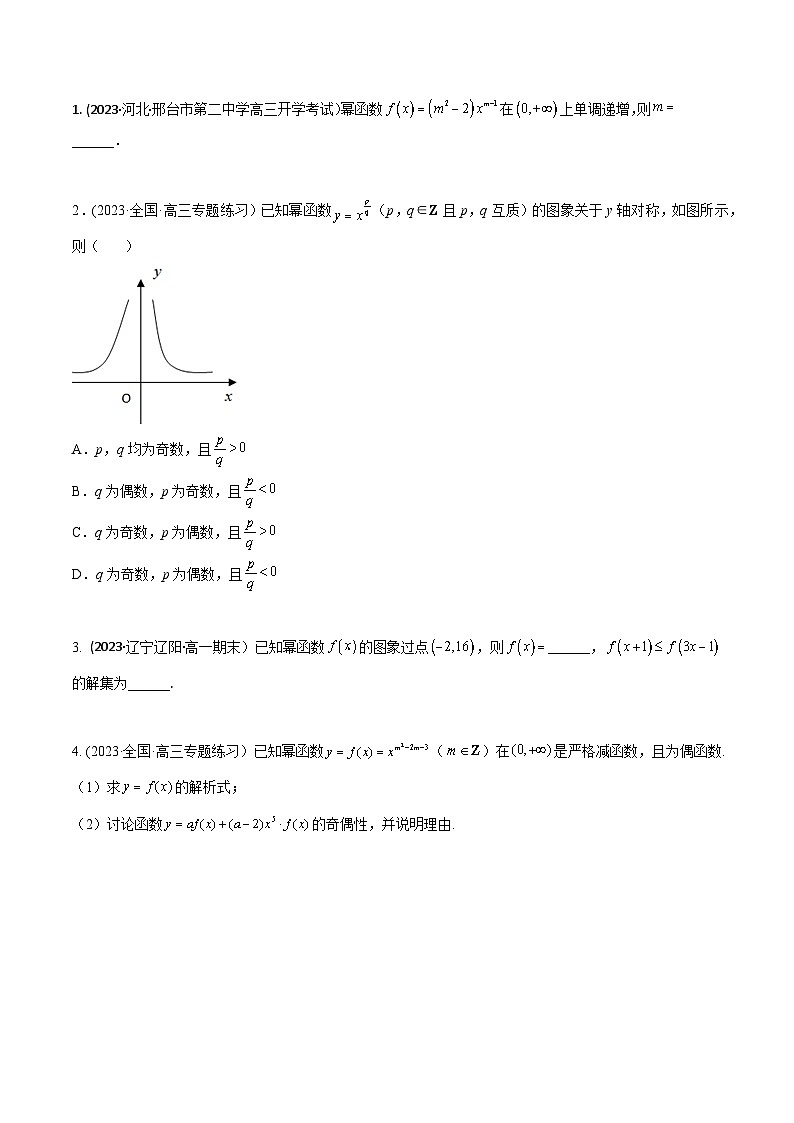
2．(2023·全国·高三专题练习）已知幂函数（p，q∈Z且p，q互质）的图象关于y轴对称，如图所示，则（ ）
A．p，q均为奇数，且
B．q为偶数，p为奇数，且
C．q为奇数，p为偶数，且
D．q为奇数，p为偶数，且
3. (2023·辽宁辽阳·高一期末）已知幂函数的图象过点，则______，的解集为______.
4. (2023·全国·高三专题练习）已知幂函数（）在是严格减函数，且为偶函数.
（1）求的解析式；
（2）讨论函数的奇偶性，并说明理由.
【题型二 二次函数的图像与性质】
例5 (2023·河南安阳·高三月考）已知二次函数，满足，.
(1)求函数的解析式；
(2)求在区间上的值域.
例6 (2023·浙江高三专题练习）若函数在内不单调，则实数a的取值范围是__________．
例7 (2023·全国高三专题练习）已知函数，函数，对于任意，总存在，使得成立，则实数a的取值范围是（ ）
A．B．C．D．
【题型精练】
1．(2023·全国·高三专题练习）已知函数，若函数在R上为减函数，则实数a的取值范围为（ ）
A．B．C．D．
2. (2023·浙江台州市·高三期末）已知函数是偶函数，则的值域是__________.
3. (2023·全国高三模拟）已知函数为定义在上的偶函数，当时，函数的最小值为1，则（ ）
A．3B．C．1D．2
【题型三 含参二次函数最值讨论】
例8 (2023·全国高三专题练习）设求函数的最小值的解析式.
例9 (2023·山东·广饶一中高三开学考试）已知函数.
(1)若，求不等式的解集；
(2)已知在上单调递增，求的取值范围；
(3)求在上的最小值.
【题型精练】
1．(2023·贵州毕节·高三月考）已知函数．
(1)当时，解关于x的不等式；
(2)函数在上的最大值为0，最小值是，求实数a和t的值．
函数
y＝ax2＋bx＋c
(a>0)
y＝ax2＋bx＋c
(a<0)
图象
(抛物线)
定义域
R
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac－b2,4a)，＋∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(4ac－b2,4a)))
对称轴
x＝－eq \f(b,2a)
顶点
坐标
eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)，\f(4ac－b2,4a)))
奇偶性
当b＝0时是偶函数，当b≠0时是非奇非偶函数
单调性
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递减；
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递增
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递增；
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递减
2.4 幂函数和二次函数
【题型解读】
【知识储备】
1．幂函数
(1)幂函数的定义
一般地，函数y＝xα叫做幂函数，其中x是自变量，α为常数．
(2)常见的五种幂函数的图象
(3)幂函数的性质
①幂函数在(0，＋∞)上都有定义；
②当α>0时，幂函数的图象都过点(1,1)和(0,0)，且在(0，＋∞)上单调递增；
③当α<0时，幂函数的图象都过点(1,1)，且在(0，＋∞)上单调递减；
④当α为奇数时，y＝xα为奇函数；当α为偶数时，y＝xα为偶函数．
2．二次函数
(1)二次函数解析式的三种形式
一般式：f(x)＝ax2＋bx＋c(a≠0)．
顶点式：f(x)＝a(x－m)2＋n(a≠0)，顶点坐标为(m，n)．
零点式：f(x)＝a(x－x1)(x－x2)(a≠0)，x1，x2为f(x)的零点．
(2)二次函数的图象和性质
【题型精讲】
【题型一 幂函数的图像与性质】
例1 (2023·江西高三月考）已知函数是幂函数，直线过点，则的取值范围是（ ）
A．B．C．D．
答案：D
【解析】由是幂函数，知：，又在上，
∴，即，则且，
∴.故选：D.
例2 (2023·全国·高三测试）图中C1、C2、C3为三个幂函数在第一象限内的图象，则解析式中指数的值依次可以是（ ）
A．、、B．、、C．、、D．、、
答案：D
【解析】由幂函数在第一象限内的图象，结合幂函数的性质，
可得：图中C1对应的，C2对应的，C3对应的，
结合选项知，指数的值依次可以是．
故选：D.
例3 (2023·黑龙江·哈九中高三开学考试）已知幂函数的图象过点，且，则a的取值范围是______．
答案：
【解析】设，
则，
所以，
在上递增，且为奇函数，
所以.
故答案为：
例4 (2023·北京人大附中高三月考）设则“的图象经过”是“为奇函数”的（ ）
A．充分不必要件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
答案：C
【解析】（1）由，
由的图像经过，则的值为，此时为奇函数.
又当为奇函数时，则的值为，此时的图象经过.
所以“的图象经过”是“为奇函数”的充要条件故选：C
（2）因为函数在上是增函数，所以，即，又因为函数在上是增函数，所以，所以，故.故选：C
【题型精练】
1. (2023·河北·邢台市第二中学高三开学考试）幂函数在上单调递增，则______．
答案：
【解析】由题意得，解得．
故答案为：.
2．(2023·全国·高三专题练习）已知幂函数（p，q∈Z且p，q互质）的图象关于y轴对称，如图所示，则（ ）
A．p，q均为奇数，且
B．q为偶数，p为奇数，且
C．q为奇数，p为偶数，且
D．q为奇数，p为偶数，且
答案：D
【解析】因函数的图象关于y轴对称，于是得函数为偶函数，即p为偶数，
又函数的定义域为，且在上单调递减，则有0，
又因p、q互质，则q为奇数，所以只有选项D正确.
故选：D
3. (2023·辽宁辽阳·高一期末）已知幂函数的图象过点，则______，的解集为______.
答案：
【解析】依题意，设，则，解得，于是得，
显然是偶函数，且在上单调递增，而，
即有，解得或，
所以的解集为.
故答案为：；
4. (2023·全国·高三专题练习）已知幂函数（）在是严格减函数，且为偶函数.
（1）求的解析式；
（2）讨论函数的奇偶性，并说明理由.
答案：（1）；（2）当时，为偶函数；当时，为奇函数；当且时，为非奇非偶函数.理由见解析.
【解析】（1）因为幂函数（）在是严格减函数，
所以，即 ，解得：，
因为，所以，
当时，，此时为奇函数，不符合题意；
当时，，此时为偶函数，符合题意；
当时，，此时为奇函数，不符合题意；
所以，
（2），
令
当时，，，此时是奇函数，
当时，，此时是偶函数，
当且时，，，
，，此时是非奇非偶函数函数.
【题型二 二次函数的图像与性质】
例5 (2023·河南安阳·高三月考）已知二次函数，满足，.
(1)求函数的解析式；
(2)求在区间上的值域.
答案：(1)(2)
【解析】(1)解：由可得，
，
由得，
所以，解得，所以.
(2)解：由（1）可得：，
则的图象的对称轴方程为，，
又因为，，
所以，在区间上的值域为.
例6 (2023·浙江高三专题练习）若函数在内不单调，则实数a的取值范围是__________．
答案：
【解析】由题意得的对称轴为，
因为函数在内不单调，所以，得．
故答案为：．
例7 (2023·全国高三专题练习）已知函数，函数，对于任意，总存在，使得成立，则实数a的取值范围是（ ）
A．B．C．D．
答案：C
【解析】因为，
所以，即的值域为[1,2]，
因为对于任意，总存在，使得成立，
所以的值域为[1,2]是在上值域的子集，
当时，在上为增函数，所以，所以，
所以，解得，
当时，在上为减函数，所以，所以
所以，解得，
综上实数a的取值范围是，
故选：C
【题型精练】
1．(2023·全国·高三专题练习）已知函数，若函数在R上为减函数，则实数a的取值范围为（ ）
A．B．C．D．
答案：B
【解析】因为函数在R上为减函数，
所以，解得，
所以实数a的取值范围为，
故选：B.
2. (2023·浙江台州市·高三期末）已知函数是偶函数，则的值域是__________.
答案：
【解析】因为是偶函数，
所以有，代入得：，解得：.
所以，
故答案为：.
3. (2023·全国高三模拟）已知函数为定义在上的偶函数，当时，函数的最小值为1，则（ ）
A．3B．C．1D．2
答案：D
【解析】由题意知，得，整理得，所以，所以，，
令，则．易知在上是增函数，所以．
因为在上的最小值是1，所以在上的最小值是1，
当时，，解得或（舍去）；
当时，，不合题意，舍去．
综上，，
故选：D．
【题型三 含参二次函数最值讨论】
例8 (2023·全国高三专题练习）设求函数的最小值的解析式.
答案：
【解析】，，
函数图像的对称轴为直线，
∴当时，即1≤t<2时，
.
当，即时，在上是减函数，
∴.
当时，在上是增函数，
∴.
综上：.
例9 (2023·山东·广饶一中高三开学考试）已知函数.
(1)若，求不等式的解集；
(2)已知在上单调递增，求的取值范围；
(3)求在上的最小值.
答案：(1)(2)(3)
【解析】(1)
解：当时，函数，
不等式，即，解得或，
即不等式的解集为.
(2)
解：由函数，可得的图象开口向上，且对称轴为，
要使得在上单调递增，则满足，
所以的取值范围为.
(3)
解：由函数，可得的图象开口向上，且对称轴为，
当时，函数在上单调递增，所以最小值为；
当时，函数在递减，在上递增，
所以最小值为；
当时，函数在上单调递减，所以最小值为，
综上可得，在上的最小值为.
【题型精练】
1．(2023·贵州毕节·高三月考）已知函数．
(1)当时，解关于x的不等式；
(2)函数在上的最大值为0，最小值是，求实数a和t的值．
答案：(1)
(2)或
【解析】(1)
当时，不等式，
即为，
即，所以，
所以或，
所以原不等式的解集为．
(2)，
由题意或，这时解得，
若，则，所以；
若，即，
所以，则，
综上，或．
2. (2023·全国高三专题练习）求二次函数在上的最小值.
答案：当时，最小值为；当时，最小值为；当时，最小值为
【解析】由题意，函数，可得在区间递减递增，
（1）当时，函数在区间递减，所以
（2）当时，在区间递增，所以
（3）当时，在区间递减，在区间递增，
所以函数
y＝ax2＋bx＋c
(a>0)
y＝ax2＋bx＋c
(a<0)
图象
(抛物线)
定义域
R
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac－b2,4a)，＋∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(4ac－b2,4a)))
对称轴
x＝－eq \f(b,2a)
顶点
坐标
eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)，\f(4ac－b2,4a)))
奇偶性
当b＝0时是偶函数，当b≠0时是非奇非偶函数
单调性
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递减；
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递增
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递增；
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递减