初中13.4课题学习 最短路径问题教学ppt课件

这是一份初中13.4课题学习 最短路径问题教学ppt课件，文件包含134课题学习最短路径问题pptx、134mp4等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

1. 通过将实际生活中的最短路径问题转化成数学中抽象的几何问题，将“路径和最小”问题用数学符号中的点、线段等表达，培养学生的模型观念．2．通过利用轴对称、平移变换解决最短路径的问题，体会图形的变换在解决最值问题中的作用，感悟化归思想．
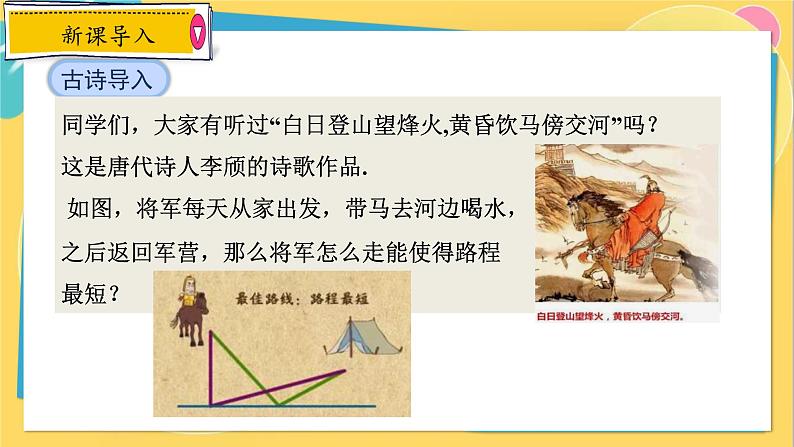
同学们，大家有听过“白日登山望烽火,黄昏饮马傍交河”吗？这是唐代诗人李颀的诗歌作品. 如图，将军每天从家出发，带马去河边喝水，之后返回军营，那么将军怎么走能使得路程最短？
请同学们观看一段视频：
同学们，在我们的生活中经常会有这样的经历，比如绿地里本来没有路，但是走的人多了，就出现了路，这是为什么呢？如果用我们的数学知识来解释这种行为，是什么呢？
我们尝试通过画图，找到最短路径．1．如图，在直线l上求作一点C，使得CA＋CB最短．
C是直线l上的一个动点．我们不妨先任意画一个点C，连接CA，CB.我们的目标：找到一个点C，使得CA＋CB最短．同学们可以观察到：当点C是线段AB和直线l的交点，即点A，C，B共线时，CA＋CB最短．依据：两点之间，线段最短
接下来，我们用这样的方法，研究数学史上经典的“将军饮马问题”．
2．请同学们阅读课本85页问题1，思考以下问题：(1)这是一个实际问题，请将实际问题抽象为数学问题．(2)和我们刚才的问题有什么不同？
图形语言：把A，B两地看成两个点，把河边l近似看成一条直线，C为直线l上的一个动点．文字语言：在直线l上求作一点C，使CA＋CB最短
点A，B在直线l的同侧
(3)能否通过图形的变换(轴对称、平移等)，将问题转化为我们研究过的问题呢？怎么转化？
能．作法如下：①作点B关于直线l的对称点B′；②连接AB′交直线l于点C；③点C即为所求的点
(4)如何证明这条路径最短？
如图，为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，只需证明AC＋CB请同学们阅读课本86页问题2.1．你能从实际背景中抽象出数学问题，构建数学模型吗？
我们可以把河的两岸看成两条平行线a和b，N为直线b上的一个动点，MN垂直于直线b，交直线a于点M，由此问题可以转化为：当点N在直线b的什么位置时，AM＋MN＋NB最小
2．能否通过图形的变换(轴对称、平移等)，将问题转化为我们研究过的问题呢？怎么转化？
将AM沿与河岸垂直的方向平移，点M移动到点N，点A移动到点A′，则AA′＝MN，AM＋NB＝A′N＋NB.这样，问题就转化为：当点N在直线b的什么位置时，A′N＋NB最小
3．利用已学知识，你能确定桥MN的位置吗？在你的数学模型中画图说明．
如图，在点N处造桥MN，所得路径最短．为了证明点N的位置即为所求，我们不妨在直线b上另外任意取一点N′，过点N′作N′M′⊥a，垂足为M′，连接AM′，A′N′，N′B，在△A′N′B中，因为A′B提疑惑：你有什么疑惑？
知识点1：最短路径问题(重点)
最短路径的求解原理：两点之间，线段最短．
注：(1)求直线异侧的两点与直线上一点所连线段和的最小值：连接两点，与直线的交点即为所求；(2)求直线同侧的两点与直线上一点所连线段和的最小值：作其中一点关于这条直线的对称点，连接对称点与另一点，与这条直线的交点即为所求．
解决“造桥选址”问题，一般用平移的方法，利用平移前后的对应线段相等，把未知的线段转移到一条直线上，再结合“两点之间，线段最短”解决问题．
知识点2：“造桥选址”问题(难点)
题型一 最短路径问题
例1：已知线段AB及直线l，在直线l上确定一点P，使PA＋PB最小．下面作图正确的是(　　)
例2：如图，在△ABC中，AB＝AC，AD，CE是△ABC的两条中线，点P是AD上的一个动点，则线段________的长度等于BP＋EP的最小值．
例3：如图，河岸CP，DQ，ER，FS互相平行，CD和EF是与河岸垂直的两座桥，A，B两点表示村庄，折线ACDEFB是A，B两村的最短路程．若∠ACP＝70°，则∠BFS的度数为(　　)A．100°　　　　　B．110°　　　　　C．120°　　　　　D．130°
题型二 造桥选址问题
本节课研究了什么问题？解决了几个问题？主要用到了什么数学知识？同学们，我们这节课的问题看似很难，实际上还是利用转化思想，转化为我们之前学过的知识，课后希望大家再回顾一下．
研究了最短路径问题和造桥选址问题．解决了两个问题．主要用到两点之间，线段最短和连接直线外一点与直线上各点的所有线段中，垂线段最短