2024辽宁中考数学二轮中考考点研究 5.4 正方形 (课件)

这是一份2024辽宁中考数学二轮中考考点研究 5.4 正方形 (课件)，共20页。PPT课件主要包含了第1题图，第2题图，第3题图，正方形与中点四边形，正方形，垂直平分且相等，中点四边形，∠ABC＝90°，∠ADC＝90°，例3题图①等内容，欢迎下载使用。

与正方形有关的证明与计算
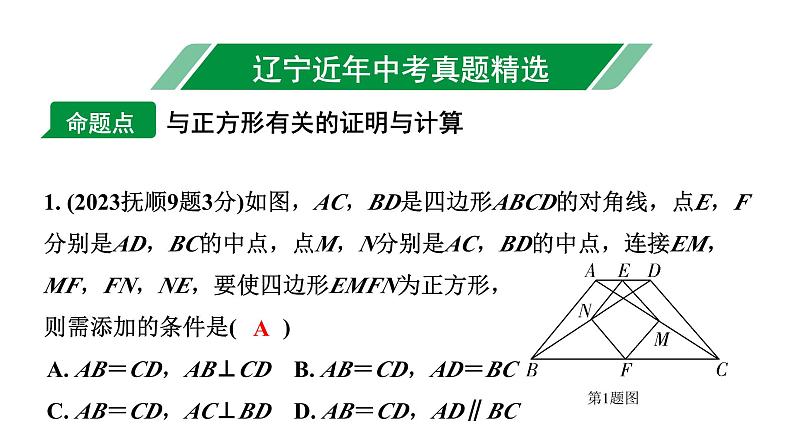
1. (2023抚顺9题3分)如图，AC，BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点，连接EM，MF，FN，NE，要使四边形EMFN为正方形，则需添加的条件是(　　)
A. AB＝CD，AB⊥CD B. AB＝CD，AD＝BCC. AB＝CD，AC⊥BD D. AB＝CD，AD∥BC
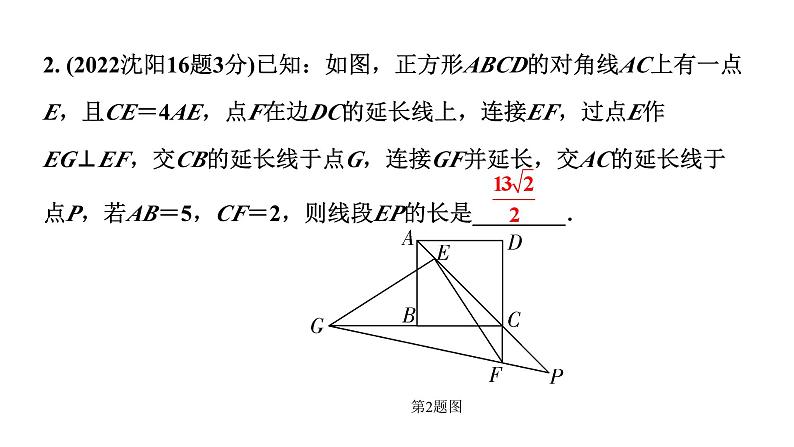
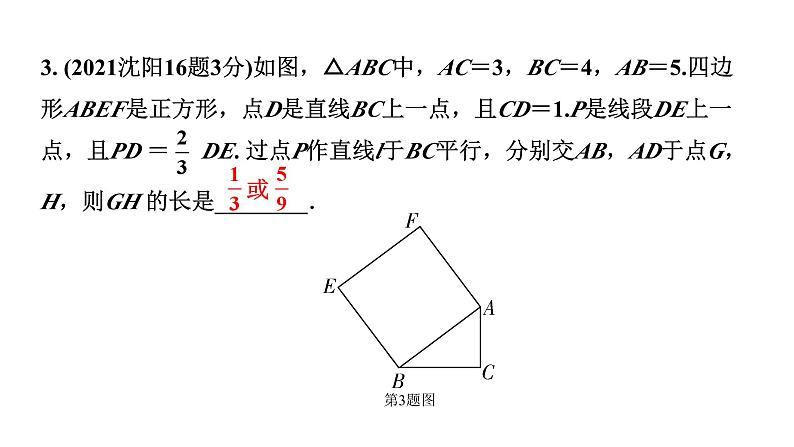
2. (2022沈阳16题3分)已知：如图，正方形ABCD的对角线AC上有一点E，且CE＝4AE，点F在边DC的延长线上，连接EF，过点E作EG⊥EF，交CB的延长线于点G，连接GF并延长，交AC的延长线于点P，若AB＝5，CF＝2，则线段EP的长是________．
【对接教材】北师：九上第一章P20～P29；人教：八下第十八章P58～P69.
1.边四条边相等,对边平行2.角：四个角都是直角3.对角线对角线相等且互相垂直平分,对角线平分一组对角4.对称性：既是轴对称图形又是中心对称图形，有　　　条对称轴
1.有一组邻边相等，并且有一个角是直角的平行四边形是正方形（定义）2.有一组邻边相等的　　　　是正方形（北师独有）3.对角线互相垂直的矩形是正方形（北师独有）4.有一个角是直角的　　　　是正方形（北师独有）5.对角线相等的菱形是正方形（北师独有）6.对角线互相　　　　　　　　的四边形是正方形
面积：S＝a2（a表示正方形边长）＝　　　　（m表示对角线的长）
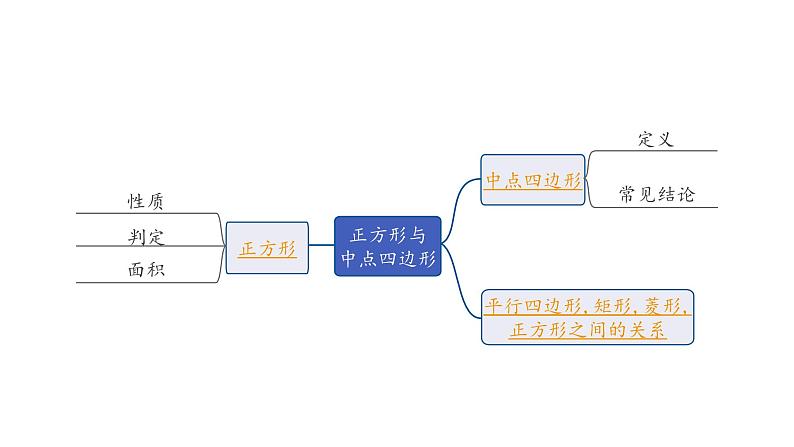
1. 定义：依次连接任意一个四边形各边中点所得的四边形叫做中点四边形2. 常见结论：
平行四边形，矩形，菱形，正方形之间的关系：
例1 四边形ABCD的对角线AC、BD相交于点O.
(1)已知AB＝AD，请添加一个条件____________(写出一个即可)，使平行四边形ABCD为正方形；
【判定依据】________________________________________________________________________________________________________．
(2)请添加一个条件________________________________________(写出一个即可)，使矩形ABCD为正方形；
【判定依据】______________________________________________．
(3)请添加一个条件______________________________________________________(写出一个即可)，使菱形ABCD为正方形．
AB＝AD或AB＝BC或AD＝DC或BC＝CD
有一组邻边相等的矩形是正方形
AC⊥BD，【判定依据】对角线互相垂直的矩形是正方形．
∠ABC＝90°或∠DAB＝90°或∠BCD＝90°或
有一个角是直角的菱形是正方形
AC＝BD，【判定依据】对角线相等的菱形是正方形
例2 四边形ABCD是正方形，对角线AC，BD相交于点O.
例3 已知在正方形ABCD中，点E、F分别是BC、CD边上的一点．
(1)如图①，若∠EAF＝45°，猜想EF、BE、DF之间的数量关系，并证明；
解：(1)EF＝BE＋DF；证明：如解图，延长CB至点M，使BM＝DF，连接AM，
(2)如图②，以点A为中心，将△ADF按逆时针方向旋转得△ABG.连接AC，FG，交于点N，点M为GF的中点，连接MB.下列结论：
(3)如解图，过点F作FK⊥CA于点K，设DF＝2x，则AP＝5x，由旋转性质得：BG＝DF＝2x，∠ABG＝∠D＝90°，
∵四边形ABCD是正方形，∴∠ABC＝90°，∠DCB＝90°，∠DCA＝45°，∴∠ABC＋∠ABG＝180°，∠ABC＝∠DCB，∴点C，B，G在同一条直线上，