
初中北师大版2 矩形的性质与判定同步达标检测题
展开1.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A. 2B. 3C. 4D. 5
2.如图,在△ABC中,∠ABC=90°,AB=8,BC=12,D为AC边上的一个动点,连接BD,E为BD上的一个动点,连接AE,CE,当∠ABD=∠BCE时,线段AE的最小值是( )
A. 3
B. 4
C. 5
D. 6
3.已知四边形ABCD的对角线相交于点O,则下列条件中不能判定它是矩形的是( )
A. AB=CD,AB//CD,∠BAD=90∘
B. AO=CO,BO=DO,AC=BD
C. ∠BAD=∠ABC=90∘,∠BCD+∠ADC=180∘
D. ∠BAD=∠BCD,∠ABC=∠ADC=90∘
4.如图,在△ABC中,∠BAC=90°,AB=8,AC=6,M为BC上的一动点,ME⊥AB于E,MF⊥AC于F,N为EF的中点,则MN的最小值为( )
A. 4.8B. 2.4C. 2.5D. 2.6
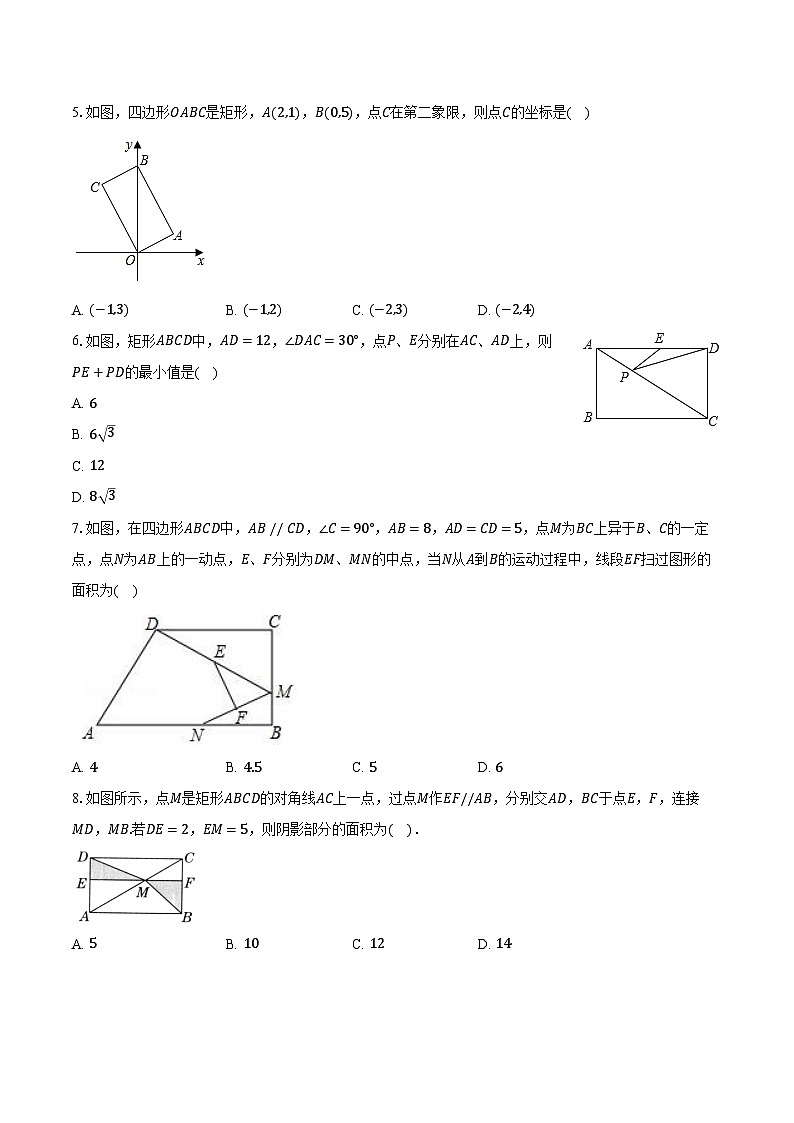
5.如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是( )
A. (−1,3)B. (−1,2)C. (−2,3)D. (−2,4)
6.如图,矩形ABCD中,AD=12,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( )
A. 6
B. 6 3
C. 12
D. 8 3
7.如图,在四边形ABCD中,AB // CD,∠C=90°,AB=8,AD=CD=5,点M为BC上异于B、C的一定点,点N为AB上的一动点,E、F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为( )
A. 4B. 4.5C. 5D. 6
8.如图所示,点M是矩形ABCD的对角线AC上一点,过点M作EF//AB,分别交AD,BC于点E,F,连接MD,MB.若DE=2,EM=5,则阴影部分的面积为( ).
A. 5B. 10C. 12D. 14
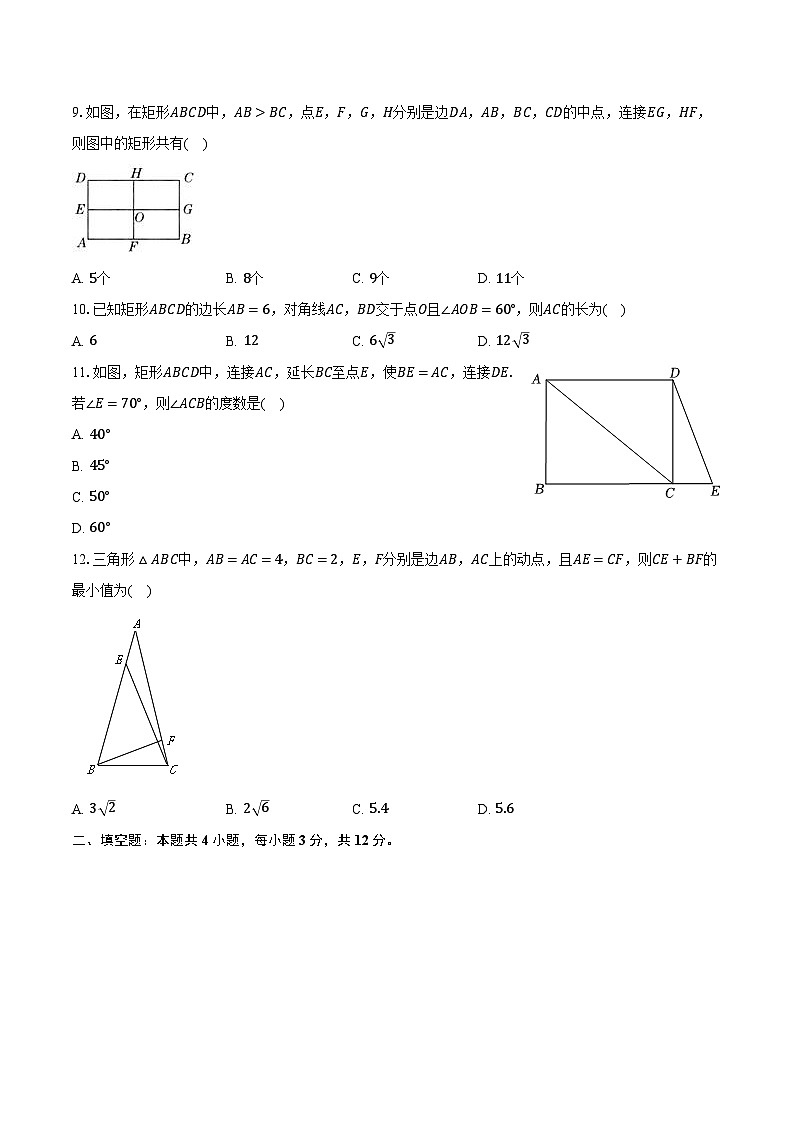
9.如图,在矩形ABCD中,AB>BC,点E,F,G,H分别是边DA,AB,BC,CD的中点,连接EG,HF,则图中的矩形共有( )
A. 5个B. 8个C. 9个D. 11个
10.已知矩形ABCD的边长AB=6,对角线AC,BD交于点O且∠AOB=60°,则AC的长为( )
A. 6B. 12C. 6 3D. 12 3
11.如图,矩形ABCD中,连接AC,延长BC至点E,使BE=AC,连接DE.若∠E=70°,则∠ACB的度数是( )
A. 40°
B. 45°
C. 50°
D. 60°
12.三角形△ABC中,AB=AC=4,BC=2,E,F分别是边AB,AC上的动点,且AE=CF,则CE+BF的最小值为( )
A. 3 2B. 2 6C. 5.4D. 5.6
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,D是AB上一点,DE⊥AC于点E,DF⊥BC于点F,连接EF,则EF的最小值为________cm.
14.如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若MF=AB,则∠DAF= ______度.
15.如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将△EBF沿EF对折后,点B落在点P处,则点P到点D的最短距离为______.
16.已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于C′,DC′交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC延长线上一点A′(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为______度.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
18.(本小题8分)
如图,在四边形ABCD中,AD//BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
(1)当运动时间为t秒时,用含t的代数式表示以下线段的长:AP=____,BQ=____;
(2)当运动时间为多少秒时,四边形PQCD为平行四边形?
(3)当运动时间为多少秒时,四边形ABQP为矩形?
19.(本小题8分)
四边形ABCD中,∠A=∠B=90°,点E在边AB上,点F在AD的延长线上,且点E与点F关于直线CD对称,过点E作EG//AF交CD于点G,连接FG,DE.
(1)求证:四边形DEGF是菱形;
(2)若AB=10,AF=BC=8,求四边形DEGF的面积.
20.(本小题8分)
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把ΔBAE沿BE向矩形内部折叠,点A的对应点A′恰好落在∠BCD的平分线上.
(1)请利用没有刻度的直尺和圆规在图①中作出点A′;(注:不写作法,保留作图痕迹)
(2)在图②中求线段CA′的长.
21.(本小题8分)
如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹)
22.(本小题8分)
在□ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点,连接AF、CH、AG、CE,AF、CE相交于点M,AG、CH相交于点N.
(1)求证:四边形AMCN是平行四边形;
(2)若四边形AMCN是矩形,连接AC、BD,则AC、BD满足的数量关系是___________.
23.(本小题8分)
如图,在矩形ABCD中,BC=6,AB=9,E为AD的中点,连接CE,过点E作CE的垂线交AB于点F,交CD的延长线于点G,连接CF.
(1)求证:CF=CG;
(2)求EF的长.
24.(本小题8分)
下面是证明直角三角形的一个性质的两种添加辅助线的方法,选择其中一种,完成证明.
25.(本小题8分)
点O为矩形ABCD的中心.
(1)命题1:如图①,过点O的直线EF⊥AC,分别交AD,BC于点E,F,则四边形AFCE是菱形.
命题2:如图②,P,Q两点在AB,CD上,且线段PQ过点O,过点O的直线EF⊥PQ,分别交AD,BC于点E,F,则四边形PFQE是菱形.
请先判断两个命题的真假,并选择一个真命题进行证明.
(2)若把图①的四边形AFCE的面积记为S1,图②的四边形PFQE的面积记为S2,则S1_________S2.(填“>”或“<”或“=”)
答案和解析
1.【答案】B
【解析】本题考查了三角形的中位线定理,直角三角形斜边上的中线,熟练掌握三角形中位线定理是解题的关键.
根据三角形中位线定理求得DE长度,再利用直角三角形斜边上的中线求得DF长度,即可得到结论.
解:∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∵BC=14,
∴DE=12BC=7,
∵∠AFB=90°,AB=8,
∴DF=12AB=4,
∴EF=DE−DF=7−4=3,
故选:B.
2.【答案】B
【解析】解:如图,取BC的中点T,连接AT,ET.
∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵∠ABD=∠BCE,
∴∠CBD+∠BCE=90°,
∴∠CEB=90°,
∵CT=TB=6,
∴ET=12BC=6,AT= AB2+BT2= 82+62=10,
∵AE≥AT−ET,
∴AE≥4,
∴AE的最小值为4,
故选:B.
如图,取BC的中点T,连接AT,ET.首先证明∠CEB=90°,求出AT,ET,根据AE≥AT−ET,可得结论.
本题考查直角三角形斜边中线的性质,勾股定理等知识,解题的关键是求出AT,ET的长,属于中考常考题型.
3.【答案】C
【解析】【分析】
本题考查的是矩形的判定定理,但考生应注意的是由矩形的判定引申出来的各图形的判定.难度一般.矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形.(2)有三个角是直角的四边形是矩形.(3)对角线互相平分且相等的四边形是矩形.据此判断.
【解答】
解:A.一个角为直角的平行四边形为矩形,故A正确;B.∵AO=CO,BO=DO,则四边形ABCD是平行四边形,又AC=BD,则四边形ABCD是矩形,故B正确;
C.∠BCD+∠ADC=180°,但∠BCD不一定与∠ADC相等,根据矩形的判定定理,故C不正确;
D.因为四边形内角和为360°,且∠BAD=∠BCD,∠ABC=∠ADC=90°,故可得到四个内角都是90°,根据矩形的判定(有三个角是直角的四边形是矩形),故D正确.
故选C.
4.【答案】B
【解析】解:过点A作AM⊥BC于点M′,
∵在△ABC中,∠BAC=90°,AB=8,AC=6,
∴BC= 82+62=10,
∴AM′=8×610=245.
∵ME⊥AB于E,MF⊥AC于F,
∴四边形AEMF是矩形,
∴AM=EF,MN=12AM,
∴当MN最小时,AM最短,此时点M与M′重合,
∴MN=12AM′=125=2.4.
故选:B.
过点A作AM⊥BC于点M′,根据勾股定理求出BC的长,再由三角形的面积公式求出AM′的长.根据题意得出四边形AEMF是矩形,故可得出AM=EF,MN=12AM,当MN最小时,AM最短,此时M与M′重合,据此可得出结论.
本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,解答时求出AM的最小值是关键.
5.【答案】D
【解析】【分析】
本题考查了矩形的性质,全等三角形的判定和性质,坐标与图形的性质,正确的作出辅助线是解题的关键.
过C作CE⊥y轴于E,过A作AF⊥y轴于F,得到∠CEO=∠AFB=90°,根据矩形的性质得到AB=OC,AB//OC,根据全等三角形的性质得到CE=AF,OE=BF,BE=OF,于是得到结论.
【解答】
解:过C作CE⊥y轴于E,过A作AF⊥y轴于F,
∴∠CEO=∠AFB=90°,
∵四边形ABCO是矩形,
∴AB=OC,AB//OC,
∴∠ABF=∠COE,
∴△OCE≌△BAF(AAS),
同理△BCE≌△OAF,
∴CE=AF,OE=BF,BE=OF,
∵A(2,1),B(0,5),
∴AF=CE=2,BE=OF=1,OB=5,
∴OE=4,
∴点C的坐标是(−2,4),
故选:D.
6.【答案】B
【解析】解:如图,将线段AD沿AC翻折得到线段AF,过点F作FH⊥AD于H,连接PF.
∵∠DAC=30°,AD=12,
由翻折可知,∠CAF=∠DAC=30°,AF=AD=12,PF=PD,
∵PD+PE=FP+PE,
又∵FP+PE≥FH,
∴PD+PD的最小值就是线段FH的长,
在Rt△AFH中,∵∠AHF=90°,∠HAF=60°,AF=12,
∴AH=6,FH=6 3,
∴PE+PD的最小值为6 3,
故选:B.
如图,将线段AD沿AC翻折得到线段AF,过点F作FH⊥AD于H,连接PF.证明PF=PD,推出PD+PE=FP+PE≥FH,求出FH即可解决问题.
本题考查轴对称最短问题,垂线段最短,矩形的性质,解直角三角形等知识,解题的关键是学会利用轴对称解决最值问题,属于中考常考题型.
7.【答案】A
【解析】【分析】
本题考查的是三角形中位线定理、勾股定理的应用,根据中位线定理得到点F的运动轨迹是解题关键.首先作出辅助线,得到点F的运动轨迹是△ABM的中位线,从而得到线段EF扫过图形即为△EFH,由中位线定理求得EH长,再结合勾股定理中位线定理求得HF边上的高EL即可.
【解答】
解:如图,连接AM,取AM,BM中点H,G,连接EH,EG,过E作EK⊥CD于K,过H作HT⊥AB于T,作DS⊥AB于S,作EL⊥HF于L.
∵E为DM中点,F为NM中点,且N在A,B之间运动,则F的运动轨迹是线段HG,即线段EF扫过图形为△EHG,
∵HG是△ABM的中位线,
∴HG=12AB=4,
∵∠C=90°,AB//CD,
∴∠B=90°,
∴四边形DCBS为矩形,
∴BS=CD=5,BC=DS,
∴AS=AB−BS=3,
由勾股定理DS=BC= 52−32=4,
∵EH分别为DM,AM中点,
∴EK,HT分别为△DCM,△ABM的中位线,
∴EK=12CM,HT=12BM,
∴EK+HT=12(CM+BM)=12BC=2,
∴EL=2,
∴△EHF的面积为12×4×2=4.
故选A.
8.【答案】B
【解析】解:如图所示,作MP⊥AB于点P,并延长PM,交DC于点Q,则四边形DEMQ、四边形QMFC、四边形AEMP、四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC−S△AMP−S△MCF=S△ADC−S△AEM−S△MQC,
∴S矩形DEMQ=S矩形MPBF.
∵DE=2,EM=5,
∴S▵DEM=S▵MFB=12×2×5=5.
∴S阴影=5+5=10.
9.【答案】C
【解析】【分析】
本题主要考查矩形的判定,难度一般.矩形是指有一个内角是直角的平行四边形.
设EG和HF相交于O,找出图中四边形DEOH、EAFO、HOGC、OFBG、DAFH、HFBC、DEGC、EABG、ABCD为矩形.
【解答】
解:设EG与HF相交于点O,
∵矩形ABCD中,点E,F,G,H分别是边DA,AB,BC,CD的中点,
∴DC//EG//AB,AD//FH//BC,
∴∠DAF=∠DEG=∠HOG=∠HFB=90°
∴四边形DEOH,EAFO,HOGC,OFBG,DAFH,HFBC,DEGC,EABG,ABCD为矩形;
则图中矩形有矩形DEOH,EAFO,HOGC,OFBG,DAFH,HFBC,DEGC,EABG,ABCD,共9个.
故选C.
10.【答案】B
【解析】【分析】
本题考查了矩形的性质,等边三角形的判定和性质,掌握矩形的性质是解题的关键.
由矩形的性质可得AC=BD,AO=BO=CO=DO,可证△AOB是等边三角形,可得AO=BO=AB=6,即可求解.
【解答】
解:∵四边形ABCD是矩形,
∴AC=BD,AO=BO=CO=DO,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AO=BO=AB=6,
∴AC=2AO=12,
故选:B.
11.【答案】A
【解析】解:连接BD,交AC于O,
∵矩形ABCD,
∴BD=AC,OB=OC,
∵BE=AC,
∴BD=BE,
∴∠BDE=∠BED=70°,
∴∠CBD=180°−∠BDE−∠BED=40°,
∵OB=OC,
∴∠ACB=∠CBD=40°.
故选:A.
连接BD,交AC于O,由矩形的性质得BD=AC,OB=OC,从而得出BD=BE,利用等边对等角求得∠BDE=∠BED=70°,从而由三角形内角和定理求得∠CBD=40°,即可由等边对等角求解.
本题考查矩形的性质,等腰三角形的性质,三角形内角和定理.正确作出辅助线,构造等腰三角形是解题的关键.
12.【答案】B
【解析】【分析】
本题主要考查的是平行线的性质,全等三角形的判定与性质,两点之间线段最短,矩形的判定和性质等有关知识.
作AG//BC,截取AG=BC,连接GE,GC,作GH⊥BC,AM⊥BC,证明△GAE≌△BCF,推出BF=EG,可得当G,E,C在同一直线上时,GE+CE=CG,此时值最小,即CE+BF的值最小,求出CG的长,可得结论.
【解答】
解:作AG//BC,截取AG=BC,连接GE,GC,作GH⊥BC交CB延长线于H,AM⊥BC与M,
∵AB=AC=4
∴∠ACB=∠ABC
∵AG//BC
∴∠GAB=∠ABC
∴∠GAE=∠BCF
∵AG=BC=2,∠GAE=∠BCF,AE=CF
∴△GAE≌△BCF
∴GE=BF
当G,E,C在同一直线上时,GE+CE=CG,此时值最小,即CE+BF的值最小
∵GH⊥BC,AM⊥BC,AG//BC
∴四边形AMHG是矩形
∴MH=AG=2,AM=GH
∵AB=AC=4,BC=2,AM⊥BC
∴CM=1,AM= 15
∴CH=3
∴CG= 15+32=2 6
∴CE+BF的最小值为2 6
13.【答案】2.4
【解析】【分析】
本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键.连接CD,根据勾股定理求出AB的长,然后证明四边形CFDE是矩形,得到EF=CD,得到当CD⊥AB时,线段EF的值最小,然后利用面积法求出CD的长即可.
【解答】
解:如图,连接CD.
∵∠ACB=90°,AC=3 cm,BC=4 cm,
∴AB= 32+42=5cm,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CFDE是矩形,
∴EF=CD.
由垂线段最短可得,当CD⊥AB时,线段CD的值最小,即线段EF的值最小,
此时,S▵ABC=12BC⋅AC=12AB⋅CD,
即12×4×3=12×5⋅CD,
解得CD=2.4 cm,
∴EF最小=2.4 cm.
14.【答案】18
【解析】解:连接DM,如图:
∵四边形ABCD是矩形,
∴∠ADC=90°.
∵M是AC的中点,
∴DM=AM=CM,
∴∠FAD=∠MDA,∠MDC=∠MCD.
∵DC,DF关于DE对称,
∴DF=DC,
∴∠DFC=∠DCF.
∵MF=AB,AB=CD,DF=DC,
∴MF=FD.
∴∠FMD=∠FDM.
∵∠DFC=∠FMD+∠FDM,
∴∠DFC=2∠FMD.
∵∠DMC=∠FAD+∠ADM,
∴∠DMC=2∠FAD.
设∠FAD=x°,则∠DFC=4x°,
∴∠MCD=∠MDC=4x°.
∵∠DMC+∠MCD+∠MDC=180°,
∴2x+4x+4x=180.
∴x=18.
故答案为:18.
连接DM,利用斜边上的中线等于斜边的一半可得△AMD和△MCD为等腰三角形,∠DAF=∠MDA,∠MCD=∠MDC;由折叠可知DF=DC,可得∠DFC=∠DCF;由MF=AB,AB=CD,DF=DC,可得FM=FD,进而得到∠FMD=∠FDM;利用三角形的外角等于和它不相邻的两个内角的和,可得∠DFC=2∠FMD;最后在△MDC中,利用三角形的内角和定理列出方程,结论可得.
本题主要考查了矩形的性质,折叠问题,三角形的内角和定理及其推论,利用三角形内角和定理列出方程是解题的关键.
15.【答案】10
【解析】【分析】
先根据勾股定理计算ED的长,当E、P、D共线时,DP最小,即最短距离是此时PD的长.
本题考查了矩形的性质,勾股定理,翻折变换的性质,利用数形结合的思想,根据图形确定点P到点D的最短距离解决问题.
【解答】
解:如图,连接PD,DE,
∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=8,BE=3,
∴AE=5,
∵AD=12,
∴DE= 52+122=13,
由折叠得:EB=EP=3,
∵EP+DP≥ED,
∴当E、P、D共线时,DP最小,
∴DP=DE−EP=13−3=10;
故答案为:10.
16.【答案】45
【解析】解:设∠EDC=x,∠GDF=y,
由折叠性质可知,∠EDG=x,∠ADF=∠CDF=2x+y,
由∠ADG=90°,得2x+y+y=90°,
∴x+y=45°,
故∠EDF=x+y=45°,
故答案为:45.
设∠EDC=x,∠GDF=y,根据折叠性质可知,∠EDG=x,∠ADF=∠CDF=2x+y,然后利用∠ADG=90°列出2x+y+y=90°求得x+y的值即可求得答案.
本题考查了长方形的性质及折叠的性质,解题的关键是了解折叠不变量,并根据题意得到2x+y+y=90°,难度中等.
17.【答案】证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形.
【解析】本题是以开放型试题,主要考查了对矩形的判定,等腰三角形的性质,及角平分线的定义等知识点的综合运用.
根据等腰三角形的性质可得AD⊥BC,∠BAD=∠CAD,又由角平分线的定义结合平角定义可得∠DAE=90°,利用已知条件和矩形判定的条件即可求证.
18.【答案】解:(1)tcm;(26−3t)cm;
(2)由题意可得:PD=AD−AP=(24−t)cm,QC=3tcm,
∵AD//BC,
∴PD//QC,
设当运动时间为t秒时PD=QC,此时四边形PQCD为平行四边形.
由PD=QC得,24−t=3t,
解得t=6,
∴当运动时间为6秒时,四边形PQCD为平行四边形.
(3)∵AD//BC,
∴AP//BQ,
设当运动时间为t秒时AP=BQ,四边形ABQP为平行四边形.
由AP=BQ得:t=26−3t,
解得:t=132,
又∵∠B=90°
∴平行四边形ABQP为矩形.
∴当运动时间为132秒时,四边形ABQP为矩形.
【解析】【分析】
此题考查了平行四边形的判定与性质以及矩形的判定与性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.
(1)根据题意可直接得出;
(2)由在四边形ABCD中,AD//BC,可得当PD=CQ时,四边形PQCD是平行四边形,即可得方程:24−t=3t,解此方程即可求得答案;
(3)由在四边形ABCD中,AD//BC,∠B=90°,可得当AP=BQ时,四边形ABQP是矩形,即可得方程:t=26−3t,解此方程即可求得答案.
【解答】
解:(1)由题意知AP=tcm,BQ=(26−3t)cm,
故答案为tcm;(26−3t)cm;
(2)见答案;
(3)见答案.
19.【答案】证明:(1)∵点E与点F关于直线 CD对称,
∴FD=ED,FG=EG,且DG=DG,
∴△FDG≌△EDG(SSS),
∴∠EDG=∠FDG,
∵EG//AF,
∴∠EGD=∠FDG,
∴∠EGD=∠EDG,
∴ED=EG,
∴FD=ED=FG=EG,
∴四边形DEGF是菱形;
(2)连接FC,EC,
∵∠A=∠B=90°,
∴AF//CB,且AF=BC=8,
∴四边形ABCF是平行四边形,且∠A=90°,
∴四边形ABCF是矩形,
∴CE=CF=AB=10,
∴BE=6,
∴AE=4,
设FD=ED=FG=EG=x,则AD=8−x,
在Rt△ADE中,42+(8−x)2=x2,
∴x=5.
∴S=5×4=20.
【解析】(1)由折叠的性质可得FD=ED,FG=EG,可证△FDG≌△EDG,可得∠EDG=∠FDG,由平行线的性质可得∠EGD=∠FDG=∠EDG,可得ED=EG,可得结论;
(2)先证四边形ABCF是矩形,可得AB=CF,由折叠的性质可得CE=CF=10,由勾股定理可求BE,AE,DF的长,即可求解.
本题考查了菱形的判定和性质,全等三角形的判定和性质,勾股定理,折叠的性质等知识,灵活运用这些性质解决是本题的关键.
20.【答案】解:(1)如图所示,点 A′ 即为所求;
(2)如图所示,过点 A′ 作 A′M⊥BC 于点 M ,
∵ 点 A 的对应点 A′ 恰落在 ∠BCD 的平分线上,
∴ 设 CM=A′M=x ,则 BM=7−x ,
又由折叠的性质知 AB=A′B=5 ,
在直角△ A′MB 中,由勾股定理得到: A′M2=A′B2−BM2=25−(7−x)2 ,
∴25−(7−x)2=x2 ,
∴x=3 或 x=4 ,
在等腰 Rt △ A′CM 中, CA′= 2A′M ,
∴CA′=3 2 或 4 2 .
【解析】本题考查了矩形的性质,翻折变换(折叠问题).解题的关键是作出辅助线,构建直角△ A′MB 和等腰直角△ A′CM ,利用勾股定理将所求的线段与已知线段的数量关系联系起来.
(1)先作 ∠BCD 的角平分线,再以点 B 为圆心,以 AB 为半径画弧,以 E 为圆心,以 AE 为半径画弧与前弧交于点 A′ ,此时点 A′ 在 ∠BCD 的平分线上;
(2)过点 A′ 作 A′M⊥BC 于点 M .设 CM=A′M=x ,则 BM=7−x .在直角△ A′MB 中,由勾股定理得到: A′M2=A′B2−BM2=25−(7−x)2 .由此求得 x 的值,然后在等腰 Rt △ A′CM 中由 CA′= 2A′M 求解即可.
21.【答案】解:(1)如图①,点F,四边形AECF即为所求作.
(2)如图②,四边形EFGH即为所求作.
【解析】(1)连接AC,BD交于点O,连接OE,延长EO交CD于点F,点F即为所求作.
(2)连接AC,BD交于点O,连接OE,延长EO交CD于点G,以O为圆心OG为半径作弧交BC于点F,延长FO交AD于点H,连接EF,FG,GH,EH,四边形EFGH即为所求.
本题考查作图−复杂作图,平行四边形的性质,矩形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.【答案】解:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB//CD,
∵E是AB的中点,
∴AE=12AB,
同理CG=12CD,
∴AE=CG,
∵AE//CG,AE=CG,
∴四边形AECG为平行四边形,
∴EC//AG.
同理AF//CH.
∵EC//AG,AF//CH,
∴四边形AMCN为平行四边形.
(2)BD=3AC.
【解析】【分析】
本题考查了平行四边形的判定与性质,矩形的性质,三角形重心性质的运用,解题的关键是掌握平行四边形的判定方法以及三角形重心性质.
(1)证明四边形AFCH是平行四边形,可得AM//CN,证明四边形AECG是平行四边形,可得EC//AG.,进而得出四边形AMCN是平行四边形;
(2)连接BD,AC,根据三角形重心的知识即可解答.
【解答】
解:(1)见答案;
(2)连接BD,AC,
在□ABCD中,AC,BD互相平分,则O为AC,BD的中点
∵M,N分别是△ABC,△ADC的重心
∴B,M,N,D在同一直线上,且BM=2OM,DN=2ON
∵四边形AMCN是矩形
∴OA=OC=OM=ON
∴BD=3OM+3ON=3MN=3AC
23.【答案】解:(1)证明:根据题意,在矩形ABCD中,则
AB=CD,BC=AD,∠A=∠EDG=90°,
∵E为AD的中点,
∴AE=DE,
∵∠AEF=∠DEG,
∴△AEF≌△DEG,
∴EF=EG,DG=AF=12;
∵CE⊥FG,
∴CG=CF;
(2)∵四边形ABCD是矩形,
∴CD=AB=9,AE=12AB=12BC=3,
∠B=90°,
设AF=x,
由(1)得:△AEF≌△DEG,
∴DG=AF=x,
∴BF=9−x,CF=CG=9+x,
在Rt△CBF中:BC2+BF2=CF2,
∴62+(9−x)2=(9+x)2,
解得:x=1,
∴AF=1,
在Rt△EAF中:EF= AF2+EF2= 12+32= 10.
【解析】本题考查了矩形的性质,全等三角形的判定与性质,垂直平分线的性质,勾股定理等知识,解得关键是熟练根据所学的知识,正确得到CG=CF
(1)由题意,先证明△AEF≌△DEG,则EF=EG,DG=AF=12,利用等腰三角形的性质,求出CG=CF;
(2)设AF=x,可得DG=AF=x,BF=9−x,CF=CG=9+x,由BC2+BF2=CF2可求AF=1,再由EF= AF2+EF2即可求解.
24.【答案】证明:方法一:∵点O 是AC 边的中点,
∴OA=OC,
又∵OD=OB,
∴四边形ABCD是平行四边形,
∵∠ABC=90∘,
∴四边形ABCD是矩形,
∴AC=BD,
∴OB=12BD=12AC.
方法二:∵ BO 是斜边AC 的中线,
∴点O是AC 的中点,
∵ BC 的中点D,
∴ OD 是△ABC的中位线,
∴OD//AB,
,
∴ OD 垂直平分线BC ,
∴OB=OC,
∵OC=12AC,
∴BO=12AC.
【解析】【分析】
本题主要考查了矩形的性质与判定,三角形中位线的性质,线段垂直平分线的性质与判定等等,灵活运用所学知识是解题的关键.
方法一:先证明四边形ABCD是平行四边形,进而证明四边形ABCD是矩形,则由矩形的性质可得OB=12BD=12AC.
方法二:证明OD 是△ABC的中位线,得到OD//AB,则OD 垂直平分BC ,由线段垂直平分线的性质可得OB=OC=12AC.
25.【答案】1)两个命题均为真命题.命题1证明如下:
证明:∵点O为矩形ABCD的中心,
∴点O是AC的中点.
∵EF⊥AC,
∴EF是AC的垂直平分线.
∴FA=FC,EA=EC,OA=OC.
∵四边形ABCD是矩形,
∴AD//BC.
∴∠EAO=∠ECO.
在△AOE和▵COF中,∠EAO=∠FCO,AO=CO,∠AOE=∠COF.
∴▵AOE≌▵COF(ASA).
∴AE=CF.
∴AE=CE=CF=AF.
∴四边形AECF为菱形.
命题2证明:如图,连接AC,则经过点O,OA=OC
∵四边形是矩形
∴AB//CD
∴∠PAO=∠CQO
又∠POA=∠QOC
∴▵POA≅▵QOC
∴OP=OQ
同命题1,可证明▵AOE≅▵COF,得OE=OF
又EF⊥PQ
∴四边形PFQE为菱形.
(2)如图,E′F′⊥AC,由图知,OC>OQ,OE′>OE
∴OE′•OC>OQ•OE
∵EF=2OE,PQ=2OQ,AC=2OC,E′F′=2OE′
∴AC•EFAC•E′F′>PQ•EF
∵S1=12AC•E′F′,S2=12PQ•EF
∴S1>S2
【解析】【分析】(1)命题1证明:由点O为矩形ABCD的中心,可证EF是AC的垂直平分线,于是FA=FC,EA=EC,OA=OC,进一步证▵AOE≌▵COF(ASA),得AE=CF,于是四边形AECF为菱形.命题2证明:连接AC,则经过点O,OA=OC,四边形是矩形,可得∠PAO=∠CQO,求证▵POA≅▵QOC,得OP=OQ,同命题1,可证明▵AOE≅▵COF,得OE=OF,得证四边形PFQE为菱形.
(2)如图,E′F′⊥AC,由图知,OC>OQ,OE′>OE,所以OE′•OC>OQ•OE,得AC•E′F′>PQ•EF,由菱形面积公式,得S1>S2.
本题考查中矩形的性质、垂直平分线的性质,菱形的判定,菱形的面积计算,全等三角形判定和性质,添加辅助线,构造全等三角形求证线段及角相等是解题的关键.
性质:直角三角形斜边上的中线等于斜边的一半.
已知:如图,在▵ABC中,∠ABC=90∘,BO 是斜边AC 的中线.
求证:BO=12AC.
方法一
证明:如图,延长BO 至点D,使得OD=OB,连接AD,CD.
方法二
证明:如图,取BC 的中点D,连接OD .
浙教版九年级上册第1章 二次函数1.1 二次函数优秀达标测试: 这是一份浙教版九年级上册<a href="/sx/tb_c12231_t7/?tag_id=28" target="_blank">第1章 二次函数1.1 二次函数优秀达标测试</a>,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学九年级上册2 矩形的性质与判定同步达标检测题: 这是一份数学九年级上册2 矩形的性质与判定同步达标检测题,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中北师大版第一章 特殊平行四边形2 矩形的性质与判定课后复习题: 这是一份初中北师大版第一章 特殊平行四边形2 矩形的性质与判定课后复习题,共39页。试卷主要包含了单选题,解答题,填空等内容,欢迎下载使用。













