初中数学沪科版八年级下册第16章 二次根式16.1 二次根式获奖课件ppt

这是一份初中数学沪科版八年级下册第16章 二次根式16.1 二次根式获奖课件ppt，文件包含沪科版数学八年级下册161《二次根式》第1课时课件pptx、沪科版数学八年级下册161《二次根式》第1课时教案docx等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。

1.什么是一个数的平方根？如何表示？
2. 平方根的性质是什么？
①16的平方根是 ； ②0的平方根是 ；③5的平方根是 ； ④–7有平方根吗？
一个正数有两个平方根，它们互为相反数；0的平方根为0；负数没有平方根.
1.什么是一个数的算术平方根？如何表示？
2. 算术平方根的性质是什么？
①16的算术平方根是 ；②0的算术平方根是 ；③5的算术平方根是 .
一个正数有一个算术平方根；0的算术平方根为0；负数没有算术平方根.
用带有根号的式子填空，看看写出的结果有什么特点？(1)如图①为正方形图片，若面积为2 m²，则边长为　 m；(2)如图②为长方形游泳池，若长是宽的2倍，面积为110 m2， 则它的宽为　　 m.
用带有根号的式子填空，看看写出的结果有什么特点？
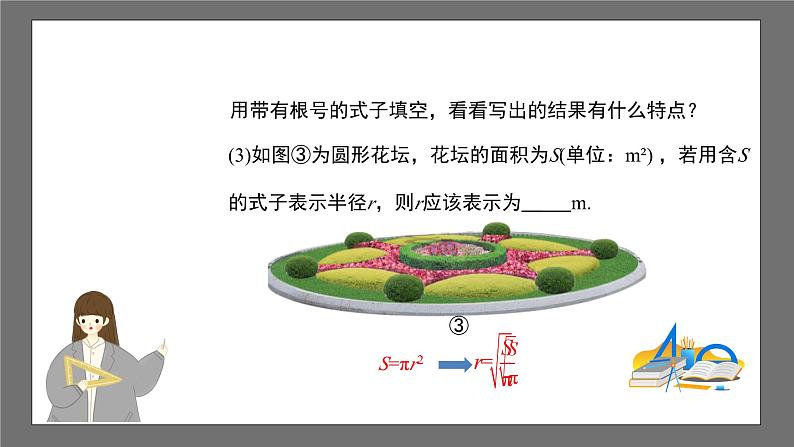
(3)如图③为圆形花坛，花坛的面积为S(单位：m²) ，若用含S的式子表示半径r，则r应该表示为　 m.
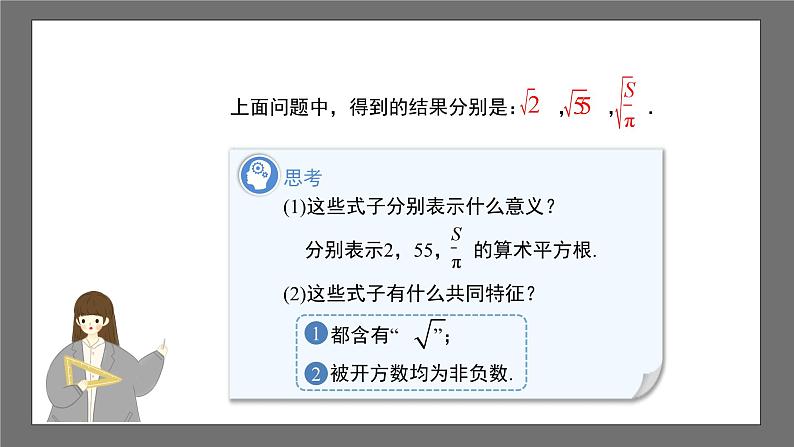
(1)这些式子分别表示什么意义？
(2)这些式子有什么共同特征？
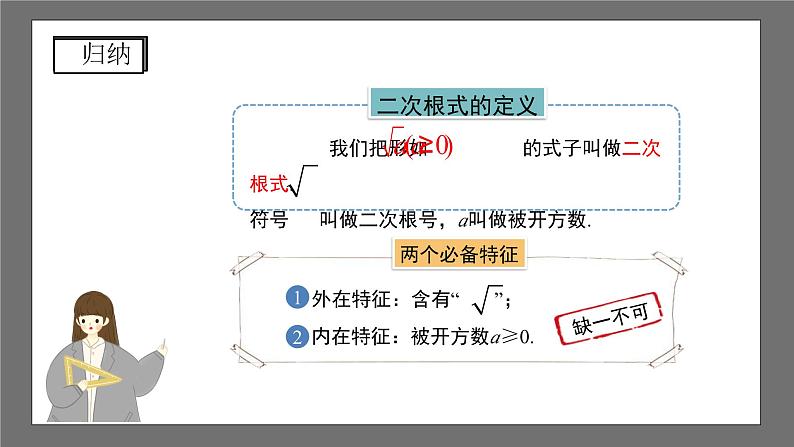
内在特征：被开方数a≥0.
下列各式中，哪些是二次根式？哪些不是？
对二次根式的进一步认识
从形式上看必须含有“ ”；二次根式实质上是非负数的算术平方根；a既可以是一个数，也可以是一个式子；a≥0，且 ；形如 的式子也是二次根式.
当a为何值时，下列根式有意义？(1) (2)
解：(1)要使 有意义，必须x+3≥0. 解这个不等式，得 x≥–3.即当x≥–3时， 在实数范围内有意义.
(2)因为x为任何实数时都有x2≥0. 所以当x为一切实数时， 在实数范围内都有意义.
【例2】当x是什么实数时，下列各式有意义？
解：(1)由x+4≥0，且 x–2≠0，得x≥– 4，且 x≠2；
(2)由–x2≥0，得x=0.
②若分母中有字母，保证分母不等于0.
1.下列各式中，哪些是二次根式？哪些不是？
解：(1)(4)是二次根式；(2)(3)(5)(6)不是二次根式.
是含二次根式的代数式，不是二次根式.
2.当x取何值时，下列式子在实数范围内有意义?
(3)由x≥0，且x–1≥0 ，可得x≥1.
二次根式有意义的条件：
若分母中有字母，保证分母不等于0.
教科书第4页习题16.1第1、2题