初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质评课课件ppt

这是一份初中数学人教版八年级上册13.1.2 线段的垂直平分线的性质评课课件ppt，共26页。PPT课件主要包含了复习引入，问题探究，例题讲解，变式练习，课堂练习，课堂小结，课后作业等内容，欢迎下载使用。

学习目标 1．能用尺规作出已知线段的垂直平分线； 2．进一步了解尺规作图的一般步骤和作图语言，理解 作图的依据； 3．能用尺规作出已知轴对称图形的对称轴； 4．能够运用尺规作图的方法解决简单的作图问题. 学习重点　　能够运用尺规作图的方法解决简单的作图问题.
复习回顾：线段垂直平分线的有关性质.
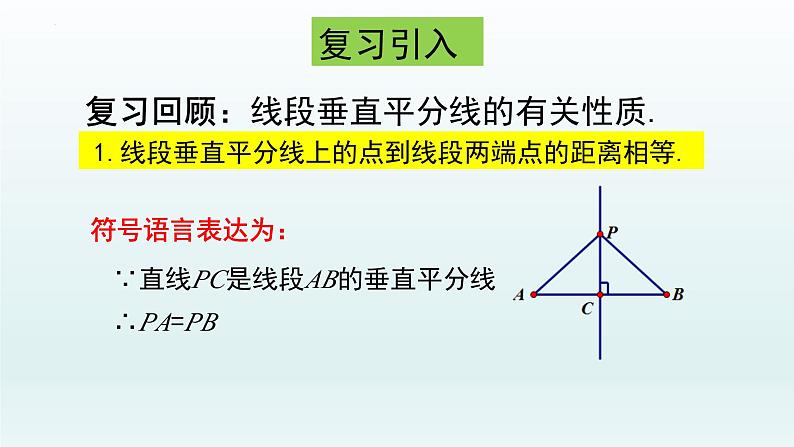
1.线段垂直平分线上的点到线段两端点的距离相等.
∵直线PC是线段AB的垂直平分线
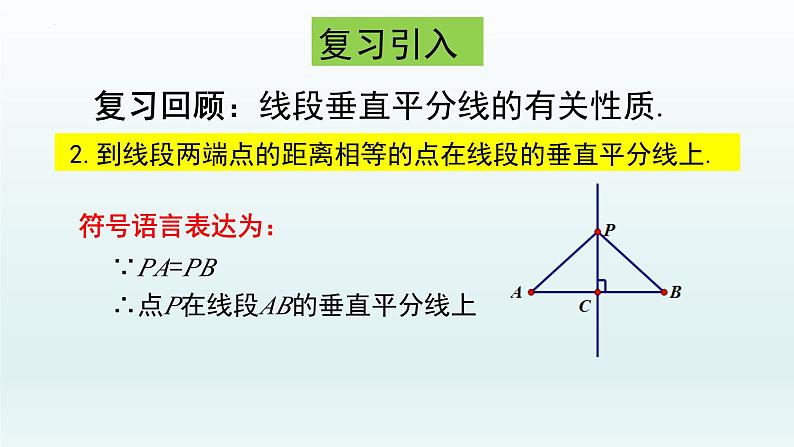
2.到线段两端点的距离相等的点在线段的垂直平分线上.
∴点P在线段AB的垂直平分线上
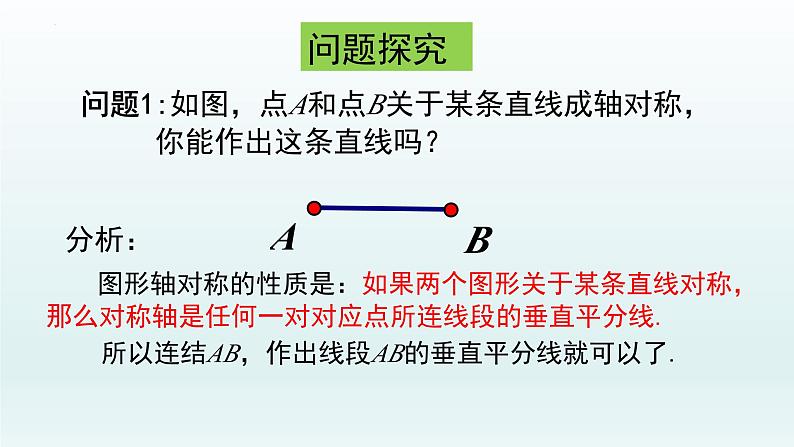
问题1:如图，点A和点B关于某条直线成轴对称， 你能作出这条直线吗？
图形轴对称的性质是：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.
所以连结AB，作出线段AB的垂直平分线就可以了.

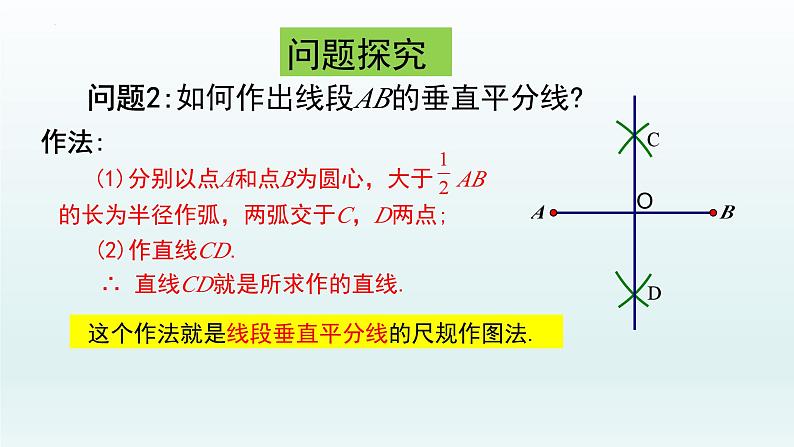
问题2:如何作出线段AB的垂直平分线呢?
因为线段垂直平分线上的点到线段两端点的距离相等.
所以要作出线段AB的垂直平分线，只要找到两个到A、B距离相等的点，点C和点D，再由两点确定一直线就可知直线CD就是线段AB的垂直平分线了.
如何找到点C和点D呢？
问题2:如何作出线段的垂直平分线?
连结CA、CB、DA、DB，
则CA=CB，DA=DB.
为了方便，我们使作点C和作点D时所取的半径相等，这样作一次弧就可以同时得到点C和点D了.再由两点确定一直线可知:直线CD就是所求作的线段AB的垂直平分线了.
问题2:如何作出线段AB的垂直平分线?
∴ 直线CD就是所求作的直线.
这个作法就是线段垂直平分线的尺规作图法.
由作图和分析可知：CD垂直平分AB，也就是说CD与AB的交点O是AB的中点，且CD⊥AB.
所以，线段垂直平分线的尺规作图法，也是线段的中点和线段的垂线的尺规作图法.
例1：尺规作图：经过已知直线外一点作这条直线的垂线
已知：直线AB和AB外一点C（如图）
观察上一探究的图形，我们可以发现：点C相当于上一探究中CD上的一点.
只要我们找到上一探究中AB对应的线段DE，然后作出线段DE的垂直平分线就可以了.
求作：AB的垂线，使它经过点C.
所以任意取一点K，使点K和点C在AB的两旁；
这时CD＝CE，点C就在线段DE的垂直平分线上.
接着再作DF=EF，则点F也在线段DE的垂直平分线上.
由两点确定一直线知：直线CF就是线段DE的垂直平分线，所以CF⊥AB.
以点C为圆心，CK的长为半径作弧，交AB于点D和点E，则DE为探究中AB对应的线段了.
变式：问：如果点C在直线AB上，那么过点C怎样作出AB的垂线？
(1)任意取一点Ｋ，使点K和点C在AB的两旁.
∴ 直线CF就是所求作的垂线.
(2)以点Ｃ为圆心，CK的长为半径作弧，交 AB于点D和点E.
已知：直线AB和AB上一点C（如图）
问：若点C在直线AB上，那么过点C怎样作出AB的垂线？
同样找到例题中的线段DE就可以了.
这时以点C为圆心，任意长为半径作弧，交AB于点D和点E，就可以得到例题中的线段DE了.
已知：直线AB和AB上一点C（如图）求作：AB的垂线，使它经过点C.
问：若点C在直线AB上，那过点C怎样作出AB的垂线？
(1)以点C为圆心，任意长为半径作弧， 交AB于点D和点E；
∴ 直线CF即为所求作的垂线.
（1）经过已知直线外一点 作这条直线的垂线
（2）经过已知直线上一点 作这条直线的垂线
归纳：这两种情况就是“经过一点作已知直线的垂线” 的所有情况.
1.如图，已知点A、点B以及直线l.用尺规作图的方法在直线l上 求作一点P，使PA＝PB.(保留作图痕迹，不要求写出作法)；
因为要使PA＝PB，所以点P在线段AB的垂直平分线上；
∴ 点P为所求作的点.
因为又要满足点P在直线l上，所以点P为线段AB的垂直平分线与直线l的交点.
2.如图，小河边有两个村庄,要在河岸边建一自来水厂向A村与B 村供水,若要使厂部到A,B的距离相等,则应选在哪里?
因为要使厂部到A,B的距离相等，所以厂部在线段AB的垂直平分线上；
∴ 点P就是厂部应选的位置.
因为厂部又要在河岸边建，因此厂部为线段AB的垂直平分线与河岸CD的交点.
3.如图，某地有两所大学和两条交叉的公路．图中点M，N表示大学，OA， OB表示公路，现计划修建一座仓库，希望仓库到两所大学的距离相等， 到两条公路的距离也相等，你能确定出仓库P应该建在什么位置吗？请 在图中画出点P的位置(保留作图痕迹，不要求写出作法)．
因为要满足仓库到两所大学的距离相等，所以仓库在线段MN的垂直平分线上；
因为又要满足仓库到两条公路的距离相等，所以仓库在∠AOB的平分线上；
因此，仓库P为线段MN的垂直平分线与∠AOB的平分线的交点.
∴ 点P就是仓库应选的位置.
厂部到A,B的距离相等
仓库到两所大学的距离相等
三题都是要作一点到两点距离相等的意思 所以都可以通过作线段的垂直平分线来解决.
作一点到两点距离相等则作线段的垂直平分线
仓库到两条公路的距离相等
作一点到角两边的距离相等则作角的平分线
4.尺规作图： 如图，五角星是轴对称图形，请作出它的一条对称轴.
所以找出这个五角星的一对对应点A和B，连结AB，作出线段AB的垂直平分线m，则直线m就是这个五角星的一条对称轴.
因为轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.
∴ 直线m即为所求作的一条对称轴.
类似地，你能作出这个五角星的其他对称轴吗？
归纳：作轴对称图形的一条对称轴的步骤
所以：直线m就是轴对称图形的一条对称轴.
(1)找出轴对称图形的一对对应点A和B;
(3)作出线段AB的垂直平分线m.
5.作出下列图形的一条对称轴，和同学比较一下，你们作出的对称轴 一样吗？
跟五角星一样，找出每个图形的一对对应点A和B，作出线段AB的垂直平分线m，则直线m就是所求作的一条对称轴了.
轴对称图形的对称轴可能是一条，也可能是两条，还可能是三条、四条甚至是无数条.轴对称图形的对称轴的条数是由图形本身的特点决定的,不一定是唯一的.
课本P64：1.练习22.习题13.1复习巩固第2题