人教版八年级上册13.1.2 线段的垂直平分线的性质背景图ppt课件

这是一份人教版八年级上册13.1.2 线段的垂直平分线的性质背景图ppt课件，共17页。PPT课件主要包含了线段的垂直平分线，PAPB，P1AP1B，本节课你有哪些收获等内容，欢迎下载使用。

在106国道某段的同侧，有两个工厂A、B，为了便于两厂的工人看病，市政府计划在公路边上修建一所医院，使得两个工厂到医院的距离相等，问医院的院址应选在何处？
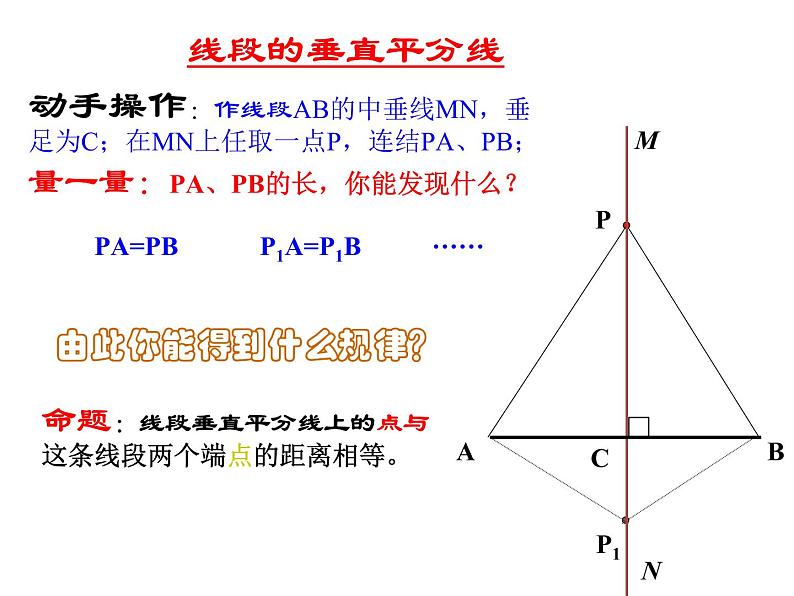
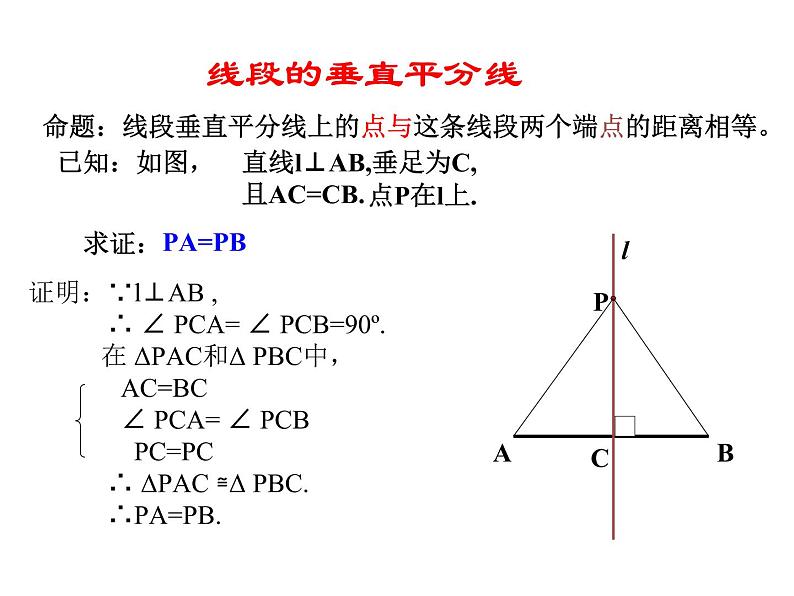
命题：线段垂直平分线上的点与这条线段两个端点的距离相等。
由此你能得到什么规律？
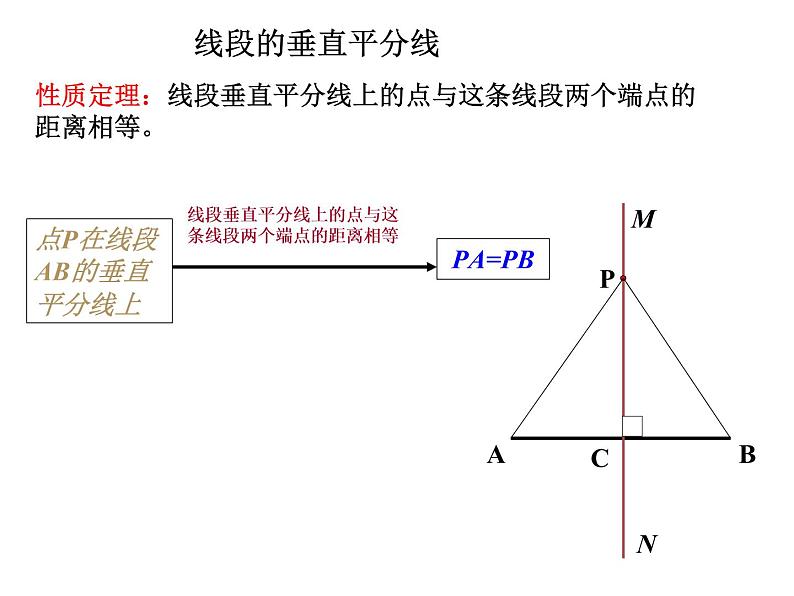
点P在线段AB的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
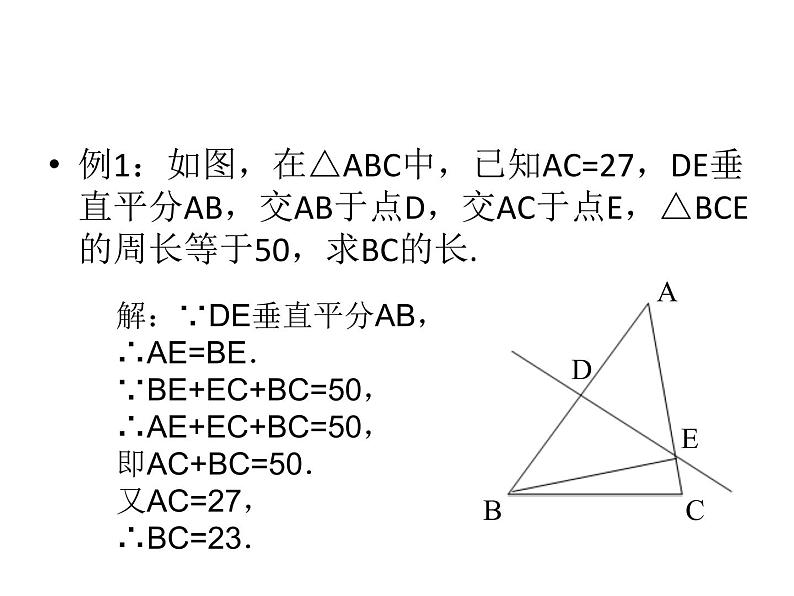
例1：如图，在△ABC中，已知AC=27，DE垂直平分AB，交AB于点D，交AC于点E，△BCE的周长等于50，求BC的长.
解：∵DE垂直平分AB，∴AE=BE．∵BE+EC+BC=50，∴AE+EC+BC=50，即AC+BC=50．又AC=27，∴BC=23．
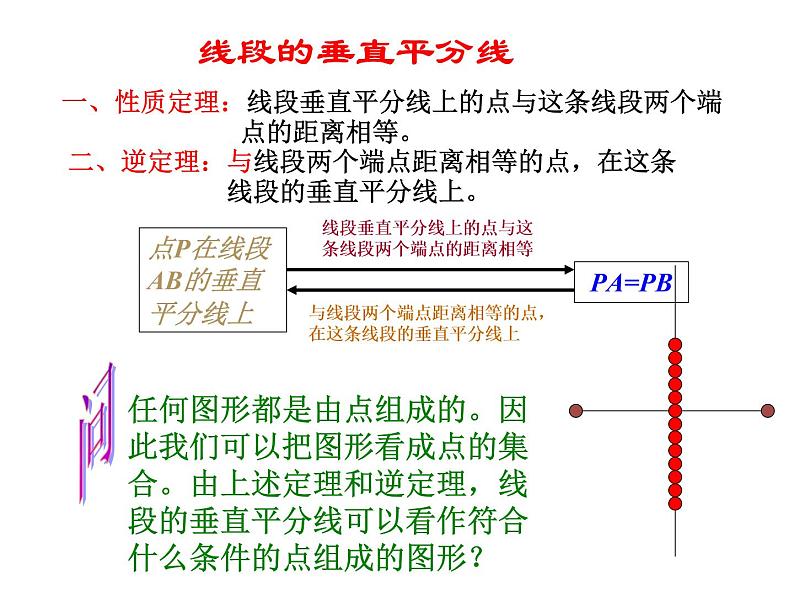
性质定理：线段垂直平分线上的点与这条线段两个端 点的距离相等。
逆命题：与一条线段两个端点距离相等的点，在这条线 段的垂直平分线上。
二、逆定理：与线段两个端点距离相等的点，在这条 线段的垂直平分线上。
线段的垂直平分线
一、性质定理：线段垂直平分线上的点与这条线段两个端 点的距离相等。
任何图形都是由点组成的。因此我们可以把图形看成点的集合。由上述定理和逆定理，线段的垂直平分线可以看作符合什么条件的点组成的图形？
三、 线段的垂直平分线的集合定义： 线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合
解：是.∵　AB =AC，∴　点A 在线段BC 的垂直平分线上．∵　MB =MC，∵　点M 在线段BC 的垂直平分线上，∴　直线AM 是线段BC 的垂直 平分线．
　　例2　如图，AB =AC，MB =MC．直线AM 是线段 BC 的垂直平分线吗？并说明理由.
在106国道某段的同侧，有两个工厂A、B，为了便于两厂的工人看病，市政府计划在公路边上修建一所医院，使得两个工厂的工人都没意见，问医院的院址应选在何处？
1.这节课你学到了哪些知识？2.你觉得这些知识在具体的题目中如何运用？3.你还有哪些困惑？
教材习题13.1第6、9题．
1．判断下列语句的对错（1）如图直线MN垂直平分线段AB，则AE=AF （ ） （2）如图线段MN被直线AB垂直平分，则ME=NE（ ）（3）如图PA=PB，则直线MN是线段AB的垂直平分线（ ）
2．在锐角△ABC内，一点P满足PA=PB=PC，则P是△ABC （ ） A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点
3．已知，D是直角△ABC斜边AC的中点，ED垂直AC于点D， ∠ EAB: ∠ EAC=2:3，求∠ ACB的度数。