八年级下册数学 专题03 梯子模型、对角互补模型和梯形中位线定理（原卷版+解析版）

这是一份八年级下册数学 专题03 梯子模型、对角互补模型和梯形中位线定理（原卷版+解析版），文件包含专题03梯子模型对角互补模型和梯形中位线定理原卷版docx、专题03梯子模型对角互补模型和梯形中位线定理解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
模型一: 如图所示,线段AC的两个端点在坐标轴上滑动，LACB= ZAOC= 90°AC的中点为P,连接 OP、BP、OB,则当 O、P、B三点共线时,此时线段 OB最大值。

即已知 RtAACB中AC、BC的长,就可求出梯子模型中 OB的最值
模型二: 如图所示,矩形ABCD 的顶点 A、B分别在边 OM、ON上,当点A在边 OM上运动时,点 B随之在 ON上运动，且运动的过程中矩形 ABCD形状保持不变，AB的中点为P,连接 OP、PD、OD,则当 O、P、D三点共线时,此时线段 OD 取最大值

四边形中对角互补模型
对角互补模型：即四边形或多边形构成的几何图形中，相对的角互补。主要分为含90°与120°的两种对角互补类型。该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形全等或者相似.
模型一：含90°的全等型
1.如图1，已知∠AOB＝∠DCE＝90º，OC平分∠AOB.则可以得到如下几个结论：
①CD＝CE，②OD＋OE＝OC，③S=S+S=OC.
2.如图2，已知∠DCE的一边与AO的延长线交于点D，∠AOB＝∠DCE＝90º，OC平分∠AOB.
则可得到如下几个结论：①CD＝CE，②OE－OD＝OC，③S-S=OC.
图1 图2 图3
模型二、：含60°与120°的全等型
如图3，已知∠AOB＝2∠DCE＝120º，OC平分∠AOB.则可得到如下几个结论：
①CD＝CE，②OD＋OE＝OC，③S+S=OC.
梯形中位线定理
（1）定义：连接梯形两腰中点的线段叫做梯形的中位线
（2）性质定理：梯形的中位线平行于两底，并且等于两底和的一半。
【类型1：梯子模型】
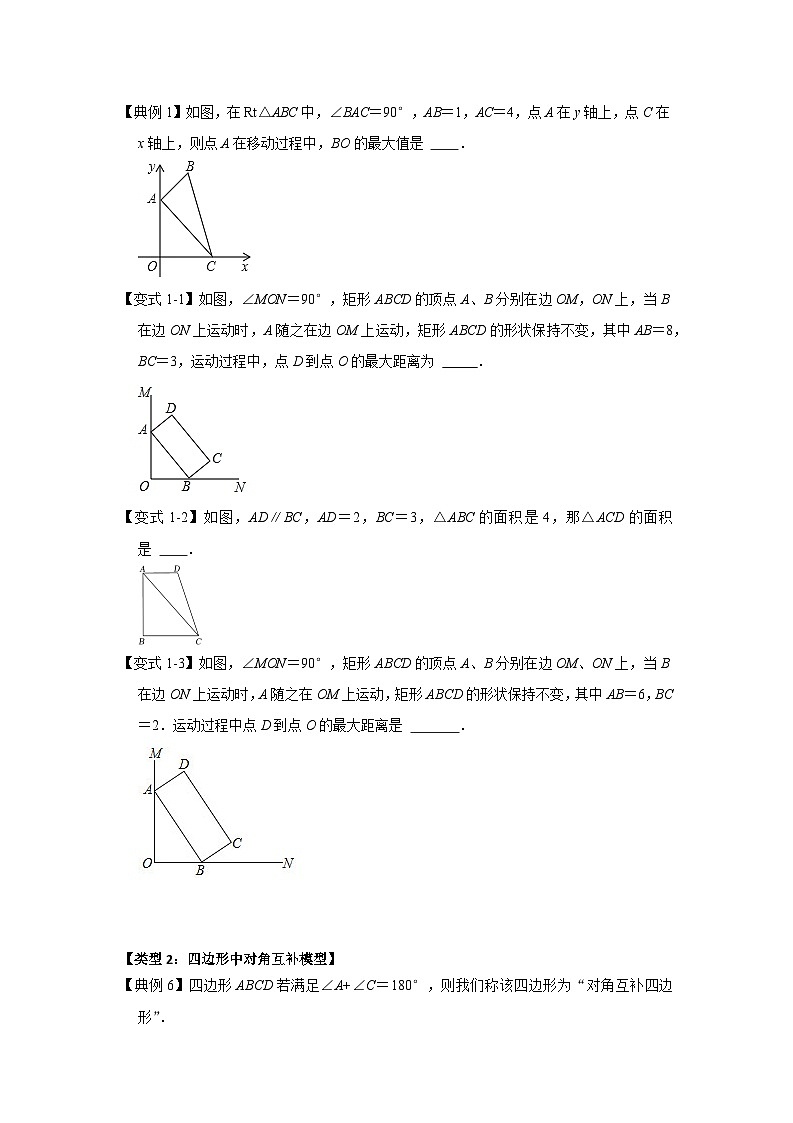
【典例1】如图，在Rt△ABC中，∠BAC＝90°，AB＝1，AC＝4，点A在y轴上，点C在x轴上，则点A在移动过程中，BO的最大值是 ．
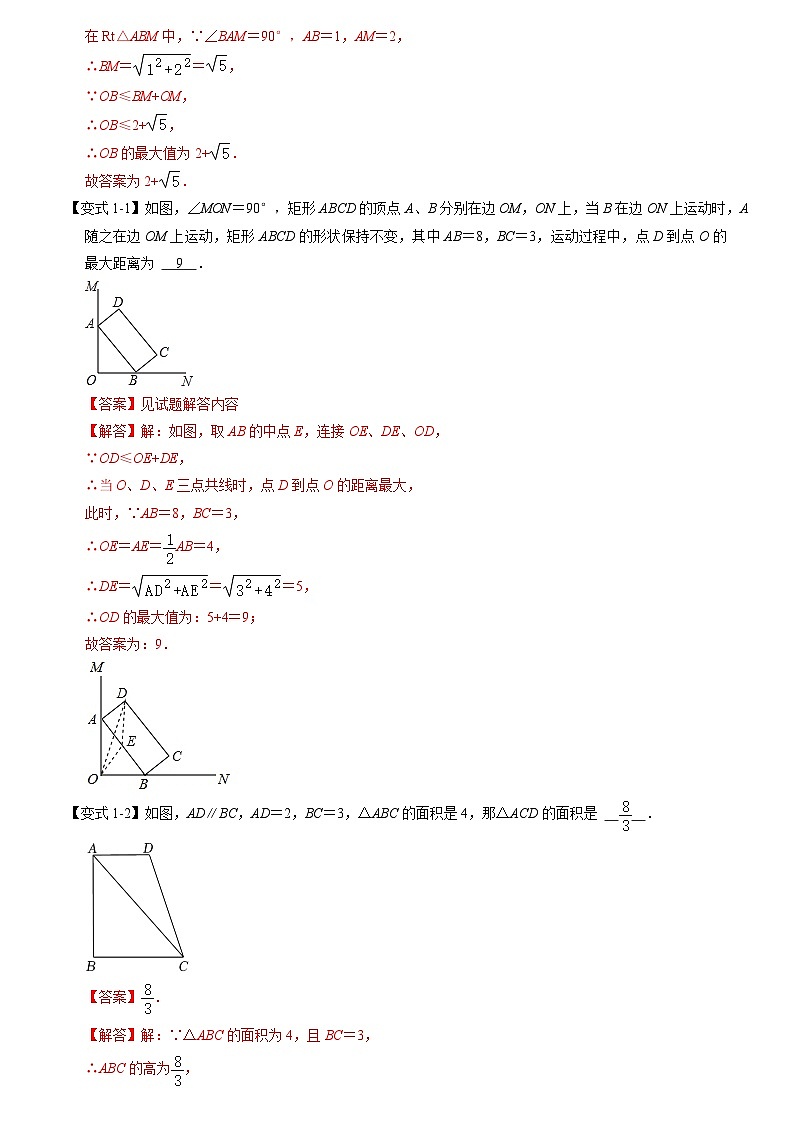
【变式1-1】如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB＝8，BC＝3，运动过程中，点D到点O的最大距离为 ．
【变式1-2】如图，AD∥BC，AD＝2，BC＝3，△ABC的面积是4，那△ACD的面积是 ．
【变式1-3】如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝6，BC＝2．运动过程中点D到点O的最大距离是 ．
【类型2：四边形中对角互补模型】
【典例6】四边形ABCD若满足∠A+∠C＝180°，则我们称该四边形为“对角互补四边形”．
（1）四边形ABCD为对角互补四边形，且∠B：∠C：∠D＝2：3：4，则∠A的度数为 ；
（2）如图1，四边形ABCD为对角互补四边形，∠BAD＝∠BCD＝90°，AB＝AD．
求证：AC平分∠BCD．
小云同学是这么做的：延长CD至M，使得DM＝BC，连AM，可证明△ABC≌△ADM，得到△ACM是等腰直角三角形，由此证明出AC平分∠BCD，还可以知道CB、CD、CA三者关系为： ；
（3）如图2，四边形ABCD为对角互补四边形，且满足∠BAD＝60°，AB＝AD，试证明：
①AC平分∠BCD；
②CA＝CB+CD；
如图3，四边形ABCD为对角互补四边形，且满足∠ABC＝60°，AD＝CD，则BA、BC、BD三者关系为： ．
、【变式2-1】四边形ABCD若满足∠A+∠C＝180°，则我们称该四边形为“对角互补四边形”．
（1）如图1，四边形ABCD为对角互补四边形，且满足∠BAD＝90°，AB＝AD，求∠ACB的度数．小云同学是这么做的：延长CB至M，使得BM＝CD，连AM，可证明△CAD≌△MAB，通过判断△MAC的形状，可以得出结论．
①在图1中按要求完成作图；
②△MAC的形状为 ；
③∠ACB＝ ；
（2）如图2，四边形ABCD为对角互补四边形，且满足∠BAD＝60°，AB＝AD，试证明：CA＝CB+CD；
（3）如图3，等腰△ABD、等腰△CDE的顶角分别为∠BAD、∠C，点B在线段CE上，且∠BAD与∠C互补．请你判断∠DAE与∠DBC的数量关系并证明．
【变式2-2】已知：在四边形ABCD中，∠A+∠C＝180°，DB平分∠ADC．
（1）求证：AB＝BC；
（2）如图2，若∠ADB＝60°，试判断△ABC的形状，并说明理由；
（3）如图3，在（2）得条件下，在AB上取一点E，BC上取一点F，连接CE、AF交于点M，连接EF，若∠CMF＝60°，AD＝EF＝7，CD＝8（CF＞BF），求AE的长．
【变式2-3】（1）探究：如图1，在△ABC和△ADE都是等边三角形，点D在边BC上．
①求∠DCE的度数；
②直接写出线段CD，CE，AC之间的数量关系；
（2）应用：如图2，在四边形ABCD中，AB＝BC，∠ABC＝60°，P是四边形ABCD内一点，且∠APC＝120°，求证：PA+PC+PD≥BD；
（3）拓展；如图3，在平面直角坐标系中，点A的坐标为（﹣4，0），点B是y轴上一个动点，以AB为边在AB的下方作等边△ABC，求OC的最小值．
【类型3：梯形中位线定理】
【典例3】如图，已知在梯形ABCD中，AB∥CD．
（1）若AD＝BC，且AC⊥BD，AC＝6，求梯形ABCD的面积；
（2）若CD＝3，M、N分别是对角线AC、BD的中点，联结MN，MN＝2，求AB的长．
【变式3-1】在梯形ABCD中，AB∥CD，AC、BD相交于点O，若AC＝5，BD＝12，中位线长为，△AOB的面积为S1，△COD的面积为S2，则＝ ．
【变式3-2】已知梯形的中位线长10cm，它被一条对角线分成两段，这两段的差为4cm，则梯形的两底长分别为 cm， cm．
17．如图，在梯形ABCD中，AD∥BC，BC＝12，AB＝DC＝8．∠B＝60°．
（1）求梯形的中位线长．
（2）求梯形的面积．
1．如图，△ABC为等边三角形，以AB为边向△ABC外侧作△ABD，使得∠ADB＝120°，再以点C为旋转中心把△CBD沿着顺时针旋转至△CAE，则下列结论：
①D、A、E三点共线；②△CDE为等边三角形；③DC平分∠BDA；④DC＝DB+DA，其中正确的有（ ）
A．4个B．3个C．2个D．1个
2．如图，正方形ABCD，点P是对角线AC上一点，连接BP，过P作PQ⊥BP，PQ交CD于Q，连接BQ交AC于G，若AP＝，Q为CD中点，则下列结论：
①∠PBC＝∠PQD；②BP＝PQ；③∠BPC＝∠BQC；④正方形ABCD的面积是16；
其中正确结论的个数是（ ）
A．4B．3C．2D．1
3．如图，∠MON＝90°，矩形ABCD的顶点A、B分别在OM、ON上，当点B在ON上移动时，点A随之移动，AB＝2，BC＝1，运动过程中，点D到点O的最大距离为 ．
4．在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝4．如图，将直角顶点B放在原点，点A放在y轴正半轴上，当点B在x轴上向右移动时，点A也随之在y轴上向下移动，当点A到达原点时，点B停止移动，在移动过程中，点C到原点的最大距离为 ．
5．如图，已知点A和点B分别是x轴正半轴，y轴正半轴上动点，且AB＝2，以B为直角顶点在第一象限作等腰直角△ABP，则点P到原点的最大距离为 ．
6．如图，Rt△AOB的两直角边OA，OB分别在x轴和y轴上，且点A，B的坐标分别是（3，0）和（0，4），点C是半圆ACB上任意一点，则点O，C的最大距离为 ．
7．在学习三角形中位线定理时，小丽发现作以下辅助线能够证明三角形中位线定理．
已知：如图1，在△ABC中，点D，E分别是边AB，AC的中点，连接DE．
求证：DE∥BC，．
证明：（小丽的辅助线作法）延长DE到F，使EF＝DE，连接DC、AF、FC．…
（1）请在图1中画出小丽所说的辅助线，并补全三角形中位线定理的证明过程；
（2）三角形中位线定理应用：如图2，在梯形ABCD中，AD∥BC，点E，F分别是AB，CD的中点，则线段AD，EF，BC之间的数量关系是 ．
8．我们规定：一组邻边相等且对角互补的四边形叫做“完美四边形”．
（1）在①平行四边形，②菱形，③矩形，④正方形中，一定为“完美”四边形的是 （请填序号）；
（2）在“完美”四边形ABCD中，AB＝AD，∠B+∠D＝180°，连接AC
①如图1，求证：AC平分∠BCD；
小明通过观察、实验，提出以下两种想法，证明AC平分∠BCD：
想法一：通过∠B+∠D＝180°，可延长CB到E，使BE＝CD，通过证明△AEB≌△ACD，从而可证AC平分∠BCD；
想法二：通过AB＝AD，可将△ACD绕点A顺时针旋转，使AD与AB重合，得到△AEB，可证C，B，E三点在一条直线上，从而可证AC平分∠BCD．
请你参考上面的想法，帮助小明证明AC平分∠BCD；
②如图2，当∠BAD＝90°，用等式表示线段AC，BC，CD之间的数量关系，并证明．
9．如图，点P（3m﹣1，﹣2m+4）在第一象限的角平分线OC上，AP⊥BP，点A在x轴正半轴上，点B在y轴正半轴上．
（1）求点P的坐标．
（2）当∠APB绕点P旋转时，
①OA+OB的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值．
②请求出OA2+OB2的最小值．
10．如图，在等边△ABC中，作∠ACD＝∠ABD＝45°，边CD、BD交于点D，连接AD．
（1）请直接写出∠CDB的度数；
（2）求∠ADC的度数；
（3）用等式表示线段AD、BD、CD三者之间的数量关系，并证明．
11．基本模型
在任意四边形中，出现一组对角互补，则为对角互补模型．
解题思路：
1．过互补角的顶点作旋转构造全等或相似；
2过互补角的顶点作双垂线构造全等或相似．
问题：
如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，BD平分∠ABC．
结论：①AD＝CD；②AB+BC＝BD；③S四边形ABCD＝BD2
请证明【基本模型】中的结论．
求证：①AD＝CD；②AB+BC＝BD；③S四边形ABCD＝BD2．
12．如图，正方形ABCD中，点E，F分别是边AB，BC上的两个动点，且正方形ABCD的周长是△BEF周长的2倍．连接DE，DF分别与对角线AC交于点M，N．
（1）若AE＝2，CF＝3，求EF的长；
（2）求证；∠EFN+∠EMN＝180°；
（3）若＝2，BE＝3，求EF的长．
13．在四边形ABCD中，△EAF的两边AE，AF分别交直线CB，DC于点E，F，已知，且AB＝AD，∠B+∠D＝180°．
（1）如图1，当△EAF全部位于四边形ABCD的内部时，试探究EF与BE，DF之间的数量关系．为了引发同学的思考，数学刘老师给出了此题的部分解法作为提示：证明：如图2，将△ABE绕点A旋转到△ADG处．
∴AE＝AG，∠BAE＝∠DAG，∠B＝∠ADG，BE＝GD，
∵∠B+∠ADC＝180°，
∴∠ADG+∠ADC＝180°，
∴G，D，F三点共线．
…
请你将上述证明过程补充完整，并写出结论；
（2）如图3，当△EAF旋转到如图所示的位置时，那么（1）中的结论是否成立？若成立，请写出证明过程；如若不成立，请写出正确的结论，并证明．
14．在四边形ABCD中，∠B+∠D＝180°，对角线AC平分∠BAD．
（1）如图1，若∠DAB＝120°，且∠B＝90°，试探究边AD、AB与对角线AC的数量关系为 ；
（2）如图2，若将（1）中的条件“∠B＝90°”去掉，（1）中的结论是否成立？请说明理由；
（3）如图3，若∠DAB＝90°，若AD＝3，AB＝7，求线段AC的长和四边形ABCD的面积．