八年级下册数学 专题02 正方形中十字架模型（原卷版+解析版）

这是一份八年级下册数学 专题02 正方形中十字架模型（原卷版+解析版），文件包含专题02正方形中十字架模型原卷版docx、专题02正方形中十字架模型解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
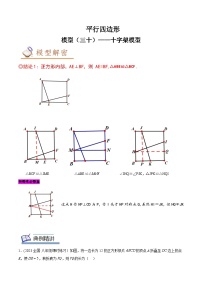
分别连接正方形的两组对边上任意两点，得到的两条线段（如：图1中的线段AF与BE，图2中的线段EF与MN，图3中的线段BE与AF）满足：若垂直，则相等。
【典例1】问题情境：苏科版八年级下册数学教材第94页第19题第（1）题是这样一个问题：
如图1，在正方形ABCD中，点E、F分别在边BC、CD上，且AE⊥BF，垂足为M．那么AE与BF相等吗？
（1）直接判断：AE BF（填“＝”或“≠”）；
在“问题情境”的基础上，继续探索：
问题探究：
（2）如图2，在正方形ABCD中，点E、F、G分别在边BC、CD和DA上，且GE⊥BF，垂足为M．那么GE与BF相等吗？证明你的结论；
问题拓展：
（3）如图3，点E在边CD上，且MN⊥AE，垂足为H，当H在正方形ABCD的对角线BD上时，连接AN，将△AHN沿着AN翻折，点H落在点H′处．
①四边形AHNH′是正方形吗？请说明理由；
②若AB＝6，点P在BD上，BD＝3BP，直接写出PH′+AN的最小值为 ．
【变式1-1】如图，在正方形ABCD中，点E、F分别在边CD，AD上，BE与CF交于点G，若BC＝4，DE＝AF＝1，则CG的长是（ ）
A．2B．C．D．
【变式1-2】如图，点E、F、G分别是正方形ABCD的边AD、BC、AB上的点，连接DG，EF，GF．且EF＝DG，DE＝2AG，∠ADG的度数为α，则∠EFG的度数为（ ）
A．αB．2αC．45°﹣αD．45°+α
【变式1-3】如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF中，正确结论的个数为（ ）
A．4个B．3个C．2个D．1个
1．在矩形纸片ABCD中，AB＝5，BC＝8，可以裁出一个最大正方形的边长是（ ）
A．4B．5C．6D．8
2．如图所示，E、F、G、H分别为正方形ABCD的边AB，BC，CD，DA上的点，且AE＝BF＝CG＝DH＝AB，则图中阴影部分的面积与正方形ABCD的面积之比为（ ）
A．B．C．D．
3．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（ ）
A．2.5B．2C．D．
4．如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE与BF相交于O；下列结论：
（1）AE＝BF；（2）AE⊥BF；（3）AD＝OE；（4）S△AOB＝S四边形DEOF．
其中正确的有（ ）
A．4个B．3个C．2个D．1个
5．如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE＝DF，AE、BF相交于点O，下列结论：①AE＝BF，②BO＝OE，③AE⊥BF，④∠ABO＝∠FAO，⑤S四边形DEOF＝S△AOB中，正确的有（ ）
A．1个B．2个C．3个D．4个
6．如图，正方形ABCD，点E，F在对角线AC上，连接BE、DF，满足BE∥DF，过点E作EG⊥DF，垂足为G，若DG＝4，EG＝3，则AD＝ ．

7．已知正方形ABCD的边长为4，CE＝DF＝3，DE和AF相交于点G，连接BG，点H是线段AE的中点，连接HG，若∠HGB＝∠DAF，则GB＝ ．
8．如图，正方形ABCD的对角线AC、BD相交于点O，M是AD上的一点，连接OM，过点O作ON⊥OM，交CD于点N，若四边形MOND的面积是3，则AB的长为 ．
9．如图，在正方形ABCD中，点E，F分别是BC，CD上的点，AE与BF相交于点G，连接AC交BF于点H．若CE＝DF，BG＝GH，AB＝2，则△CFH的面积为 ．
10．如图，四边形ABCD是正方形，点E、N分别在DC、BC上，点F在CB的延长线上．△ADE≌△DCN，将△ADE顺时针旋转n度后，恰好与△ABF重合．
（1）请写出n的值；
（2）连结EF，试求出∠AFE的度数；
（3）猜想线段AE和DN的数量关系和位置关系，并说明理由．
11．【探索发现】（1）如图1，正方形ABCD的对角线相交于点O，点O又是正方形A1B1C1O的一个顶点，而且这两个正方形的边长相等，我们知道，无论正方形A1B1C1O绕点O怎么转动，总有△AEO≌△BFO，连接EF，求证：AE2+CF2＝EF2；
【类比迁移】（2）如图2，矩形ABCD的中心O是矩形A1B1C1O的一个顶点，A1O与边AB相交于点E，CO与边CB相交于点F，连接EF，矩形A1B1C1O可绕着点O旋转，判断（1）中的结论是否成立，若成立，请证明，若不成立，请说明理由；
【迁移拓展】（3）如图3，在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝4cm，直角∠EDF的顶点D在边AB的中点处，它的两条边DE和DF分别与直线AC，BC相交于点E，F，∠EDF可绕着点D旋转，当BF＝1cm时，直接写出线段EF的长度．
12．如图，已知四边形ABCD是正方形，点F是DC边上的动点（不与端点重合），点E在线段AF上，AD＝m2+1，AE＝2m，DE＝m2﹣1，M为线段BF的中点，点N在线段AF上（不与点F重合），且MN＝BF．
（1）求证：BN⊥AF；
（2）随着点F的运动，试猜想AB﹣AN的值是否是发生变化，若不变，请求出定值，若变化，请说明理由．
13．（1）如图1，在正方形ABCD中，AE、DF相交于点O且AE⊥DF则AE和DF的数量关系为 ．
（2）如图2，在正方形ABCD中，E、F、G分别是边AD、BC、CD上的点，BG⊥EF，垂足为H．求证：EF＝BG．
（3）如图3，在正方形ABCD中，E、F、M分别是边AD、BC、AB上的点，AE＝2，BF＝5，BM＝1，将正方形沿EF折叠，点M的对应点恰好与CD边上的点N重合，求CN的长度．
14．（1）如图①，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过A点作AG⊥EB，垂足为G，求证：OE＝FO；
（2）如图②，若点E在AC的延长线上，AG⊥EB，交EB的延长线于G．AG的延长线交DB的延长线于F，其他条件不变，则结论“OE＝OF”还成立吗？若成立，请给予证明，若不成立，请说明理由．
15．综合与实践：
如图，在正方形ABCD中，点E是边AB上的一个动点（点E与点A，B不重合），连接CE，过点B作BF⊥CE于点G，交AD于点F．
（1）如图1，求证：△ABF≌△BCE；
（2）如图2，当点E运动到AB中点时，连接DG，求证：DC＝DG；
（3）如图3，若AB＝4，连接AG，当点E在边AB上运动的过程中．AG是否存在最小值，若存在，请直接写出AG最小值，及此时AE的值；若不存在，请说明理由．
16．如图1，P为正方形ABCD的边BC上一动点（P与B、C不重合），点Q在CD边上，且BP＝CQ，连接AP、BQ交于点E．
（1）求证：AP⊥BQ；
（2）当P运动到BC中点处时（如图2），连接DE，请你判断线段DE与AD之间的关系，并说明理由；
（3）如图3，在（2）的条件下，过A点作AM⊥DE于点H，交BQ、CD于点N、M，若AB＝2，求QM的长度．
17．如图，在正方形ABCD中，E是边AB上的点，连接CE，过点D作DF⊥CE，分别交BC，CE于点F、G．
（1）求证：CE＝DF；
（2）若AB＝3，图中阴影部分的面积和与正方形ABCD的面积之比为2：3，则△DCG的面积为
，CG+DG的长为 ．
18．如图1，已知正方形ABCD和正方形AEFG有公共顶点A，连接BE，DG．
（1）请判断BE与DG的数量关系与位置关系，并证明你的结论．
（2）如图2，已知AB＝4，，当点F在边AD上时，求BE的长．
19．如图1，在正方形ABCD中，，点E在边BC上，连接AE，且∠BAE＝30°，点F是AE的中点．
（1）求AE的长；
（2）过点F作直线GH，分别交AB，CD于点G，H，且GH＝AE，求AG的长；
（3）如图2，过点F作AE的垂线，分别交AB，BD，CD于点M，O，N，连接OE，求∠AEO的度数．
20．如图，Rt△ABC两条外角平分线交于点D，∠B＝90°，过点D作DE⊥BA于点E，DF⊥BC于点F．
（1）求证：四边形BFDE是正方形；
（2）若BF＝6，点C为BF的中点，直接写出AE的长．
21．在正方形ABCD中，P是边BC上一动点（不与点B、C重合），E是AP的中点，
过点E作MN⊥AP，分别交AB、CD于点M，N．
（1）判定线段MN与AP的数量关系，并证明；
（2）连接BD交MN于点F．
①根据题意补全图形；
②用等式表示线段ME，EF，FN之间的数量关系，直接写出结论 EF＝EM+FN ．
22．如图1，正方形ABCD中，点P为线段BC上一个动点，若线段MN垂直AP于点E，交线段AB于M，CD于N，证明：AP＝MN；
如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB、AP、BD、DC于点M、E、F、N．
（1）求证：EF＝ME+FN；
（2）若正方形ABCD的边长为2，则线段EF的最小值＝ ，最大值＝ ．