2024年高中数学(必修第一册)5.3诱导公式精品讲义(学生版+解析)

这是一份2024年高中数学(必修第一册)5.3诱导公式精品讲义(学生版+解析)，共10页。

1 诱导公式
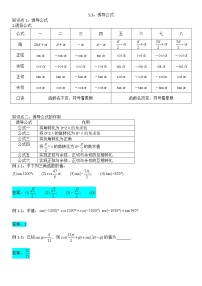
(1) 公式(一) sinα+2kπ=sinα; cs (α+2kπ)=cs α ; tan (α+2kπ)=tan α.
(2) 公式(二) sin (π+α)=−sin α ; cs (π+α)=−cs α ; tan (π+α)=tan α.
若P1(x , y)，则P2(−x , −y).
(3) 公式(三) sin (−α)=−sin α ; cs (−α)=cs α ; tan (−α)=−tan α.
若P1(x , y)，则P3(x , −y).
(4) 公式(四) sin (π−α)=sin α ; cs (π−α)=−cs α ; tan (π−α)=−tan α.
若P1(x , y)，则P4(−x , y).
(5) 公式(五) sin (π2−α)=cs α ; cs (π2−α)=sin α.
若P1(x , y)，则P5(y , x).
(6) 公式(六) sin (π2+α)=csα ; cs (π2+α)=−sin α.
若P1(x , y)，则P6(−y , x).
利用以上6组公式，最好结合图象，利用对称性和全等三角形进行理解消化.
2 诱导公式口诀：奇变偶不变，符号看象限
(奇偶指的是π2∙n+α中整数n是奇数还是偶数，看象限时把α看作锐角)
sin π2∙n+α= (−1)n2 sin α , n为偶数−1n+12cs α , n为奇数 cs (π2∙n+α)= (−1)n2 cs α , n为偶数−1n+12sin α , n为奇数

【题型一】求具体角度的三角函数值
【典题1】 sin780°+cs210°+tan225°的值为 ．

【题型二】诱导公式的使用
【典题1】 设f(n)=cs(nπ2+π4)，则f(1)+f(2)+f(3)+…+f(2018)等于 ．
【典题2】 已知cs(π6−α)=34，则sin(α−2π3)= ．
【典题3】 已知g(θ)=cs(−θ−π2)⋅sin(7π2+θ)sin(2π−θ)．
(1)化简g(θ)；
(2)若g(π3+θ)=13 , θ∈(π6 , 7π6)，求g(5π6+θ)的值；
(3)若g32π−θ−g(θ)=13 , θ∈(−π2 , π2)，求gθ−g(π2−θ)的值．
巩固练习
1(★) 若sinα=45，则 ( )
A．csπ2−α=45 B．sinπ2−α=35
C．sin(π+α)=45 D．sin(π−α)=−45
2(★) 在△ABC中，下列等式一定成立的是 ( )
A．sinA+B=−sinCB．csA+B=csC
C．csB+C2=sinA2D．sinB+C2=sinA2
3(★) sin(−17π6)+cs(−20π3)+tan(−53π6)= ．
4(★★) 已知sin(α−π3)=13，则cs(π6+α)= ．
5(★★) 已知sinθ , csθ是关于x的方程x2−ax+a=0(a∈R)的两个根．
(1)求cs3(π2−θ)+sin3(π2−θ)的值；
(2)求tan(π−θ)−1tanθ的值．


挑战学霸
sin21°+sin22°+sin23°+…+sin289°= .

诱导公式
1 诱导公式
(1) 公式(一) sinα+2kπ=sinα; cs (α+2kπ)=cs α ; tan (α+2kπ)=tan α.
(2) 公式(二) sin (π+α)=−sin α ; cs (π+α)=−cs α ; tan (π+α)=tan α.
若P1(x , y)，则P2(−x , −y).
(3) 公式(三) sin (−α)=−sin α ; cs (−α)=cs α ; tan (−α)=−tan α.
若P1(x , y)，则P3(x , −y).
(4) 公式(四) sin (π−α)=sin α ; cs (π−α)=−cs α ; tan (π−α)=−tan α.
若P1(x , y)，则P4(−x , y).
(5) 公式(五) sin (π2−α)=cs α ; cs (π2−α)=sin α.
若P1(x , y)，则P5(y , x).
(6) 公式(六) sin (π2+α)=csα ; cs (π2+α)=−sin α.
若P1(x , y)，则P6(−y , x).
利用以上6组公式，最好结合图象，利用对称性和全等三角形进行理解消化.
2 诱导公式口诀：奇变偶不变，符号看象限
(奇偶指的是π2∙n+α中整数n是奇数还是偶数，看象限时把α看作锐角)
sin π2∙n+α= (−1)n2 sin α , n为偶数−1n+12cs α , n为奇数 cs (π2∙n+α)= (−1)n2 cs α , n为偶数−1n+12sin α , n为奇数

【题型一】求具体角度的三角函数值
【典题1】 sin780°+cs210°+tan225°的值为 ．
【解析】 sin780°+cs210°+tan225°
=sin(720°+60°)+cs(180°+30°)+tan(180°+45°)
=sin60°−cs30°+tan45°
=32−32+1=1.
【点拨】角度负角化正角，大角化小角，小角化锐角.

【题型二】诱导公式的使用
【典题1】 设f(n)=cs(nπ2+π4)，则f(1)+f(2)+f(3)+…+f(2018)等于 ．
【解析】∵f(n+4)=cs[(n+4)π2+π4]=cs(nπ2+π4) ,
∴f(n)是以4为周期的函数，
又f(1)=−22 , f(2)=−22 , f(3)=22 , f(4)=22 ,
∴f1+f2+f3+…+f2018
=504f1+f2+f3+f4+f1+f2=−2．
【点拨】数值比较大项数比较多的时候，注意周期性.
【典题2】 已知cs(π6−α)=34，则sin(α−2π3)= ．
【解析】∵cs(π6−α)=34，
∴sinα−2π3=sin−π2−π6−α=−cs(π6−α)=−34.
【点拨】
① 注意到(π6−α)+(α−2π3)=−π2是π2的倍数，则可利用诱导公式，这属于整体代换，相当于令π6−α=t.
② 对公式的理解要注意一点:比如诱导公式sin (π2+α)=cs α中的α其实它可以是一数(如π4、π3)、一字母(如β、θ)或者一式子(如α2、β+π3)，利用公式要特别灵活.
【典题3】 已知g(θ)=cs(−θ−π2)⋅sin(7π2+θ)sin(2π−θ)．
(1)化简g(θ)；
(2)若g(π3+θ)=13 , θ∈(π6 , 7π6)，求g(5π6+θ)的值；
(3)若g32π−θ−g(θ)=13 , θ∈(−π2 , π2)，求gθ−g(π2−θ)的值．
【解析】 1 g(θ)=cs(θ+π2)sin(4π−π2+θ)sin(−θ)=−sinθ(−csθ)−sinθ=−csθ；
2∵θ∈π6 , 7π6， ∴π3+θ∈(π2 , 3π2)，
∵gπ3+θ=−cs(π3+θ)=13 ，即cs(π3+θ)=−13；
∴g5π6+θ=−cs5π6+θ=−cs(π2+π3+θ)=sin(π3+θ)；
∴当π3+θ∈(π2 , π)时，
g(5π6+θ)= sin(π3+θ)=1−cs2(π3+θ)=223；
当π3+θ∈(π , 3π2)，
g(5π6+θ) =sin(π3+θ)=−1−cs2(π3+θ)=−223；
(3) gθ−gπ2−θ=−csθ+csπ2−θ=sinθ−csθ
由g32π−θ−g(θ)=13，得−cs(32π−θ)+csθ=13，
整理得sinθ+csθ=13，
两边平方得：sinθ+csθ2=1+2sinθcsθ=19，即2sinθcsθ=−89<0，
∴sinθ－csθ2=1－2sinθcsθ=179⇒sinθ−csθ=±173，
∵θ∈(−π2 , π2)，
∴csθ>0 , sinθ<0，即sinθ－csθ <0，
则gθ−gπ2−θ=173．作
【点拨】在解题中综合法与分析法相结合.
巩固练习
1(★) 若sinα=45，则 ( )
A．csπ2−α=45 B．sinπ2−α=35
C．sin(π+α)=45 D．sin(π−α)=−45
【答案】 A
【解析】若sinα=45，所以cs(π2−α)=sinα=45，sin(π2−α)=csα=±35，
sin(π+α)=−sinα=−45，sin(π−α)=sinα=45．
故选：A．
2(★) 在△ABC中，下列等式一定成立的是 ( )
A．sinA+B=−sinCB．csA+B=csC
C．csB+C2=sinA2D．sinB+C2=sinA2
【答案】 C
【解析】在△ABC中，有A+B+C=π，
∴sin(A+B)=sinC，故A错误；cs(A+B)=﹣csC，故B错误；
csB+C2=cs(π−A2)=sinA2，故C正确；sinB+C2=sin(π−A2)=csA2，故D错误．
∴等式一定成立的是C．故选：C．
3(★) sin(−17π6)+cs(−20π3)+tan(−53π6)= ．
【答案】 −1+33
【解析】sin−17π6+cs−20π3+tan−53π6
=－sinπ6+cs4π3−tan5π6=−12−12+33=−1+33；
4(★★) 已知sin(α−π3)=13，则cs(π6+α)= ．
【答案】 −13
【解析】∵sin(α−π3)=13，
∴cs(π6+α)=cs[π2+(α−π3)]=－sin(α−π3)=−13，
5(★★) 已知sinθ , csθ是关于x的方程x2−ax+a=0(a∈R)的两个根．
(1)求cs3(π2−θ)+sin3(π2−θ)的值；
(2)求tan(π−θ)−1tanθ的值．
【答案】 (1) 1−2 (2) 2+1
【解析】依题意，△=－a2－4a≥0，解得a≥4或a≤0，
又sinθ+csθ=asinθ⋅csθ=a，
所以sinθ+csθ2=1+2sinθcsθ，即a2－2a－1=0，
解得a=1−2或a=1+2(舍去)，
因此sinθ+csθ=sinθcsθ=1−2．
(1)cs3(π2−θ)+sin3(π2−θ)
=sin3θ+cs3θ=(sinθ+csθ)(1－sinθcsθ)
=(1−2)[1－(1−2)]=2−2．
(2)tan(π－θ)−1tanθ=−sinθcsθ−csθsinθ=−sin2θ+cs2θsinθcsθ=−11−2=2+1．
挑战学霸
sin21°+sin22°+sin23°+…+sin289°= .
【解析】设S=sin21°+sin22°+sin23°+…+sin289° ①
又∵S=sin289°+sin288°+sin287°+…+sin21°
=cs21°+cs22°+cs23°+…+cs289° ②
由①+②得 2S=89，则S=892．