2021年新高考数学名校地市选填压轴题好题汇编（十九）（原卷版+解析版）

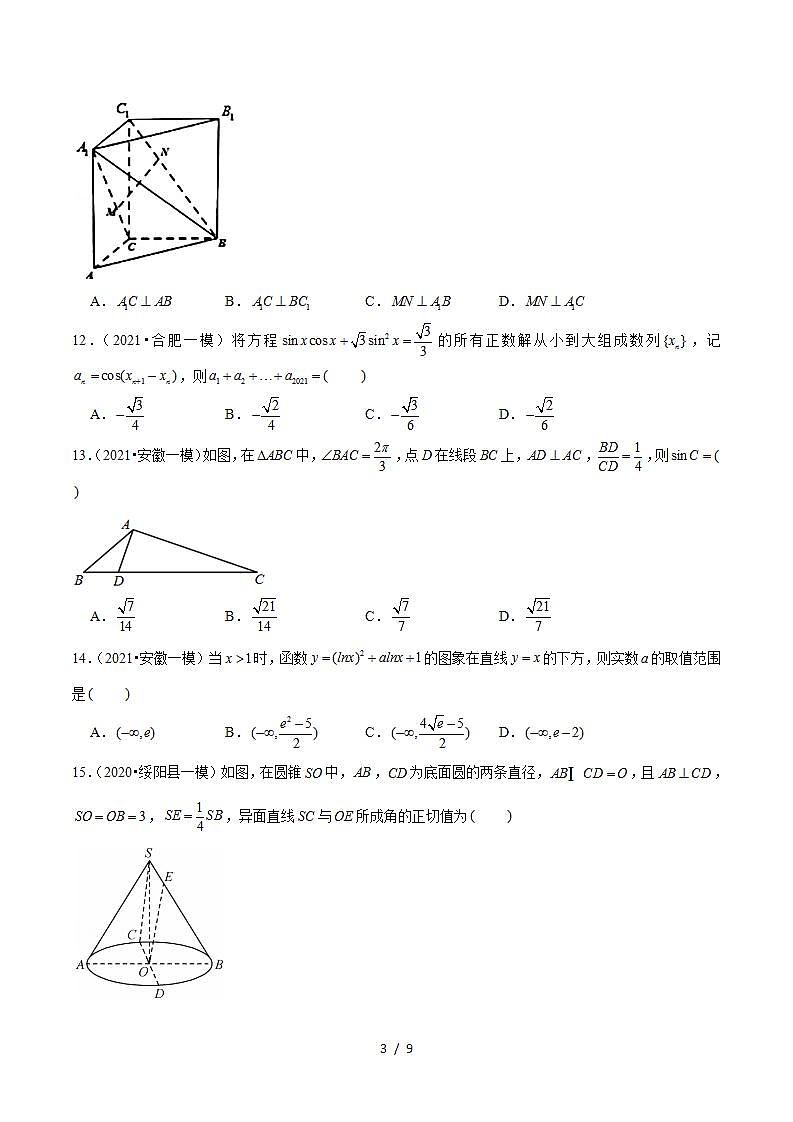
2021年新高考数学名校地市选填压轴题好题汇编（十九）一．选择题（共23小题）1．（2021•福州一模）分形几何学是一门以不规则几何形态为研究对象的几何学．如图，有一列曲线，，，．已知是边长为1的等边三角形，是对进行如下操作而得到：将的每条边三等分，以每边中间部分的线段为边，向外作等边三角形，再将中间部分的线段去掉，1，2，．记的周长为、所围成的面积为对于，下列结论正确的是　　A．为等差数列 B．为等比数列 C．，使 D．，使2．（2021•福州一模）已知函数，图象过，在区间上为单调函数，把的图象向右平移个单位长度后与原来的图象重合．设，且，若，则的值为　　A． B． C．1 D．3．（2021•泉州一模）已知曲线，直线与有且只有4个公共点、这些公共点从左到右依次为，，，，设，，，，则下列结论中错误的是　　A．或 B． C． D．4．（2021•厦门一模）已知双曲线的中心为，圆与双曲线的一条渐近线交于，两点．若，则双曲线的离心率为　　A． B． C． D．5．（2021•安庆二模）设抛物线的焦点为，过点作倾斜角为的直线交抛物线于点，（点位于轴上方），是坐标原点，记和的面积分别为，，则　　A．9 B．4 C．3 D．26．（2021•安庆二模）《九章算术》卷五《商功》中，把正四棱台形状的建筑物称为“方亭”，沿“方亭”上底面的一组对边作垂直于底面的两截面，去掉截面之间的几何体，将“方亭”的两个边角块合在一起组成的几何体称为“刍甍”．现记截面之间几何体体积为，“刍甍”的体积为，若，台体的体积公式为，其中、分别为台体的上、下底面的面积．则“方亭”的上、下底面边长之比为　　A． B． C． D．7．（2021•安庆二模）已知，且，的夹角为，若向量，则的取值范围是　　A．， B． C．， D．，8．（2021•安庆二模）对任意，，使得不等式成立的最大整数为　　A． B． C．0 D．19．（2021•安庆二模）设直三棱柱的所有顶点都在一个球面上，且球的体积是，，，则此直三棱柱的高是　　A． B．4 C． D．10．（2021•安庆二模）若曲线在点，（1）处的切线与直线平行，且对任意的，，，不等式恒成立，则实数的最大值为　　A． B． C． D．11．（2021•合肥一模）我国古代数学名著《九章算术》第五卷“商功”中，把底面为直角三角形的直三棱柱称为堑堵．如图，在堑堵中，，，分别是线段，上的点，且，，则下列说法正确的是　　A． B． C． D．12．（2021•合肥一模）将方程的所有正数解从小到大组成数列，记，则　　A． B． C． D．13．（2021•安徽一模）如图，在中，，点在线段上，，，则　　A． B． C． D．14．（2021•安徽一模）当时，函数的图象在直线的下方，则实数的取值范围是　　A． B． C． D．15．（2020•绥阳县一模）如图，在圆锥中，，为底面圆的两条直径，，且，，，异面直线与所成角的正切值为　　A． B． C． D．16．（2021•浙江模拟）已知函数，若，其中，则的最小值为　　A． B． C． D．17．（2021•浙江模拟）已知数列满足，则一定成立的是　　A． B． C． D．18．（2021•浙江模拟）如图，在中，，，，将绕边翻转至，使平面平面，是的中点，设是线段上的动点，则当与所成角取得最小值时，线段等于　　A． B． C． D．19．（2021•浙江模拟）如图，三棱锥的侧棱长都相等，底面与侧面都是以为斜边的等腰直角三角形，为线段的中点，为直线上的动点，若平面与平面所成锐二面角的平面角为，则的最大值是　　A． B． C． D．20．（2021•浙江模拟）已知椭圆，，分别是椭圆的左、右焦点，是椭圆的下顶点，直线交椭圆于另一点，若，则椭圆的离心率为　　A． B． C． D．21．（2020•诸暨市校级模拟）已知数列满足，，，则　　A．当时， B．当时， C．当时， D．当时，22．（2020•诸暨市校级模拟）已知函数，若恒成立，则实数的取值范围是　　A．， B．， C．， D．，23．（2021•1月份模拟）已知正六棱锥，是侧棱上一点（不含端点），记直线与直线所成角为，直线与平面所成角为，二面角的平面角为，则　　A．， B．， C．， D．，二．多选题（共5小题）24．（2021•福州一模）已知是双曲线在第一象限上一点，，分别是的左、右焦点，△的面积为．则以下结论正确的是　　A．点的横坐标为 B． C．△的内切圆半径为1 D．平分线所在的直线方程为25．（2021•福州一模）在数学中，双曲函数是一类与三角函数类似的函数．最基本的双曲函数是双曲正弦函数和双曲余弦函数等．双曲函数在物理及生活中有着某些重要的应用，譬如达芬奇苦苦思索的悬链线（例如固定项链的两端，使其在重力的作用下自然下垂，那么项链所形成的曲线即为悬链线）问题，可以用双曲余弦型函数来刻画．则下列结论正确的是　　A． B．为偶函数，且存在最小值 C．， D．，，且，26．（2021•泉州一模）已知函数，，则　　A．在上为增函数 B．当时，方程有且只有3个不同实根 C．的值域为 D．若，则，27．（2021•泉州一模）如图，已知正四棱柱的底面边长为1，侧棱长为2，点，分别在半圆弧，（均不含端点）上，且，，，在球上，则　　A．当点在的中点处，三棱锥的体积为定值 B．当点在的中点处，过，，三点的平面截正四棱柱所得的截面的形状都是四边形 C．球的表面积的取值范围为 D．当点在的三等分点处，球的表面积为28．（2021•厦门一模）已知函数，，若函数有3个不同的零点，，，且，则的取值可以是　　A． B． C． D．三．填空题（共22小题）29．（2021•福州一模）已知圆的方程为，过点的直线与圆交于，两点（点在第四象限）．若，则点的纵坐标为　　．30．（2021•福州一模）在三棱锥中，侧面与底面垂直，，，，．则三棱锥的外接球的表面积为　　．31．（2021•泉州一模）圆锥曲线光学性质（如图1所示）在建筑、通讯、精密仪器制造等领域有着广泛的应用．如图2，一个光学装置由有公共焦点，的椭圆与双曲线构成，一光线从左焦点发出，依次经过与的反射，又回到点历时秒；若将装置中的去掉，则该光线从点发出，经过两次反射后又回到点历时秒，若与的离心率之比为，则　　．32．（2021•泉州一模）若正数，满足，则的最小值为　　．33．（2021•厦门一模）已知三棱锥的四个顶点，，，均在球的球面上，，是边长为4的等边三角形，，分别是，的中点，，则　　，球的表面积是　　．34．（2021•厦门一模）已知直线与抛物线相交于，两点，抛物线的焦点为，则　　．35．（2021•安庆二模）已知，分别为双曲线的左、右焦点，过点作的一条渐近线的垂线，垂足为．连接，设直线，的斜率分别为，，若，则双曲线的离心率为　　．36．（2021•安庆二模）钝角的面积是，，，角的平分线交于点，则　　．37．（2021•安庆二模）已知函数，，为的一个零点，为图象的一条对称轴，且在，内不单调，则的最小值为　　．38．（2021•合肥一模）已知双曲线的两个焦点分别为，，是双曲线渐近线上一点，，点满足，且，则该双曲线的离心率等于　　．39．（2021•安徽一模）如图，，分别为双曲线的右顶点和右焦点，过作轴的垂线交双曲线于，且在第一象限，，，到同一条渐近线的距离分别为，，，且是和的等差中项，则的离心率为　　．40．（2021•安徽一模）如图，在三棱锥中，是边长为1的等边三角形，，点，，分别在棱，，上，平面平面，若，则三棱锥的外接球被平面所截的截面面积为　　．41．（2021•浙江模拟）已知实数，满足，则的最大值为　　．42．（2021•浙江模拟）是边长为6的正三角形，点满足，且，，，则的取值范围是　　．43．（2021•浙江模拟）已知直线与圆，若，直线与圆相交于，两点，则　　，若直线与圆相切，则实数　　．44．（2021•浙江模拟）中，，且对于，最小值为，则　　．45．（2021•浙江模拟）已知三边长分别为3，，，是平面内任意一点，则的最小值是　　．46．（2021•浙江模拟）已知圆，过点作两条互相垂直的直线，，其中交该圆于，两点，交该圆于，两点，则的最小值是　　，的最大值是　　．47．（2020•诸暨市校级模拟）如图，在直角三角形中，，，，为内一点，且，设，若，则　　；若，则　　．48．（2020•诸暨市校级模拟）已知函数，若，则的最大值是　　．49．（2020•诸暨市校级模拟）已知斜率为1的直线经过椭圆的左焦点，且与椭圆交于，两点，若椭圆上存在点，使得的重心恰好是坐标原点，则椭圆的离心率　　．50．（2020•诸暨市校级模拟）已知平面向量，，，若，且，则的取值范围是　　．