初中数学人教版九年级上册22.1.1 二次函数授课课件ppt

这是一份初中数学人教版九年级上册22.1.1 二次函数授课课件ppt，共25页。PPT课件主要包含了二次函数，一次函数，正比例函数，从特殊，到一般，描点法画图，观察图象特征，归纳函数性质，yx2，图象开口向上等内容，欢迎下载使用。

1.用描点法画二次函数y=ax2的图象，知道抛物线y=ax2是轴对称图形，知道抛物线y=ax2的开口方向与a的符号有关.
2.能根据图象说出抛物线y=ax2的开口方向、对称轴、顶点坐标，能根据a的符号说出顶点是抛物线的最高点还是最低点.
二次函数y=ax2+bx+c(a，b，c是常数，a≠0)
最简单的二次函数y=ax2
画二次函数 y=x2 的图象.
1.列表：在y = x2中，自变量x可以是任意实数.
用平滑曲线，自左向右顺次连接，向两端无限延伸.
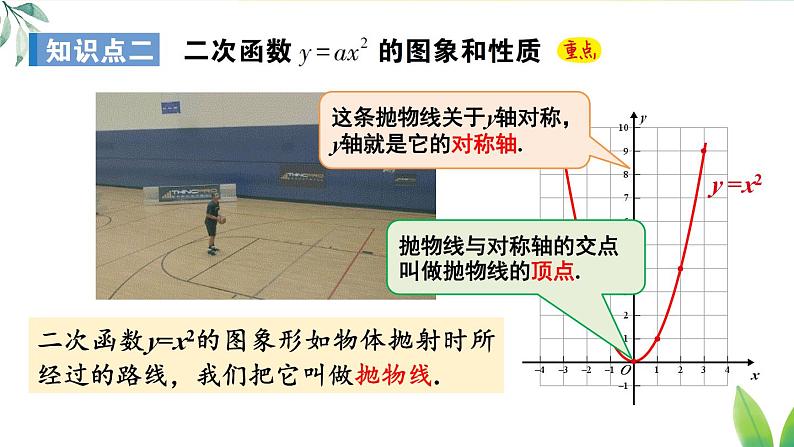
二次函数y=x2的图象形如物体抛射时所经过的路线，我们把它叫做抛物线.
这条抛物线关于y轴对称，y轴就是它的对称轴.
抛物线与对称轴的交点叫做抛物线的顶点.
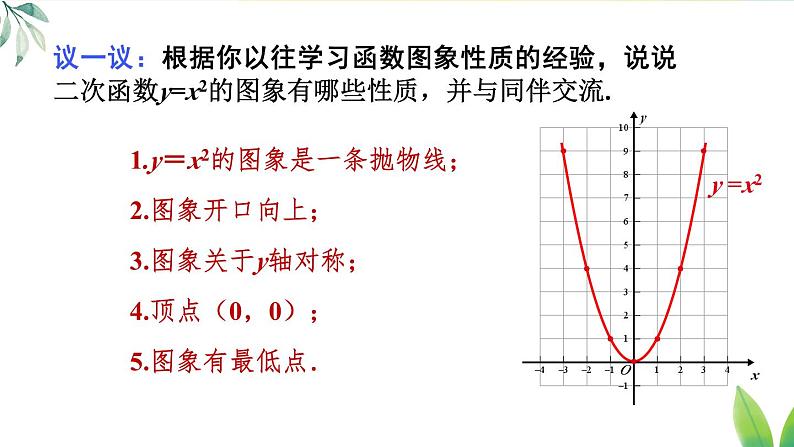
议一议：根据你以往学习函数图象性质的经验，说说二次函数y=x2的图象有哪些性质，并与同伴交流.
1.y＝x2的图象是一条抛物线；
3.图象关于y轴对称；
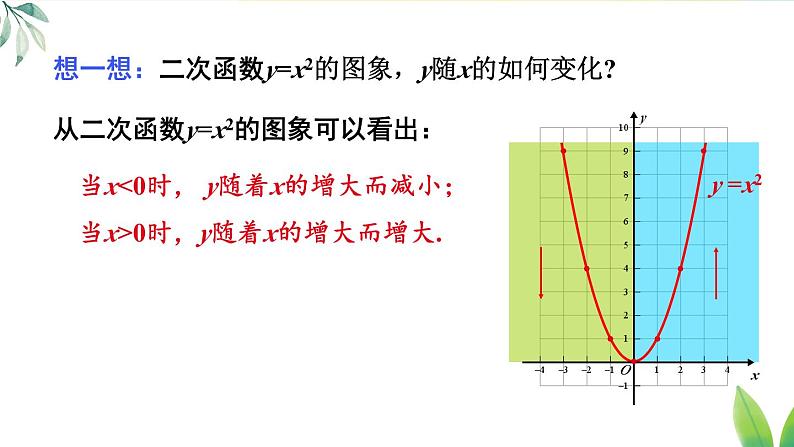
想一想：二次函数y=x2的图象，y随x的如何变化?
从二次函数y=x2的图象可以看出：
当x<0时， y随着x的增大而减小；
当x>0时，y随着x的增大而增大.
思考：（1）函数y= x2 ，y=2x2的图象与函数y=x2的图象相比，有什么共同点和不同点？
④顶点是抛物线的最低点；
⑤当x<0时， y随着x的增大而减小；当x>0时，y随着x的增大而增大.
思考：（2）当a>0时，二次函数y=ax2的图象有什么特点？
⑥a越大，抛物线的开口越小.
思考：（1）从函数y= x2 ，y=-x2，y=-2x2的图象，考虑这些抛物线有什么共同点和不同点？
④顶点是抛物线的最高点；
⑤当x<0时， y随着x的增大而增大；当x>0时，y随着x的增大而减小.
思考：（2）当a<0时，二次函数y=ax2的图象有什么特点？
⑥a越小，抛物线的开口越小.
说出下列抛物线的开口方向、对称轴和顶点： （1）y = 3x2；（2）y = -3x2 ；（3）y = x2；（4）y = - x2.
观察右面图象，抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数，开口相反，大小相同，它们关于x轴对称.
1. 函数y=2x2的图象的开口_______，对称轴是_______，顶点是________ . 在对称轴的左侧，y随x的增大而_______，在对称轴的右侧，y随x的增大而_______.
2. 函数y=-5x2的图象的开口_______，对称轴是_______，顶点是________ . 在对称轴的左侧，y随x的增大而_______，在对称轴的右侧，y随x的增大而_______.
3.如右图，观察函数y=(k-1)2的图象，则k的取值范围是_______.
4.已知下列二次函数 ①y=-x2；②y= x2；③y=15x2；④y=-4x2；⑤y=4x2.（1）其中开口向上的是________（填序号）；（2）其中开口向下且开口最大的是______（填序号）；（3）有最高点的是_______（填序号）.
5.若抛物线y=ax2(a≠0)，过点(-1，2).（1）则a的值是_______；（2）对称轴是_______，开口_______.（3）顶点坐标是_______，顶点是抛物线上的最_______点.抛物线在x轴的_______方(除顶点外).（4）若A(x1，y1)，B(x2，y2)在这条抛物线上，且x16.已知一次函数y=ax+b和二次函数y=ax2，其中a≠0，b<0，则下面选项中，图象可能正确的是（ ）
7.如图，二次函数y=2x2的图象经过点(0，0)，长方形ABCD的顶点A、B在x轴上，C、D恰好在二次函数的图象上，B点的横坐标为2，求图中阴影部分的面积之和．
解：∵二次函数y=2x2的图象经过点C，
∴当x=2时，y=2×22=8，即BC=8.
∵抛物线和长方形都是轴对称图形，且y轴为它们的对称轴，
∴在长方形ABCD内，左边阴影部分面积等于右边空白部分面积.
∴S阴影部分面积之和=2×8=16.
二次函数y=ax2的图象和性质
以对称轴为中心对称取点