

2023-2024学年甘肃省武威十七中教研联片七年级(下)第一次月考数学试卷(3月份)(含解析)
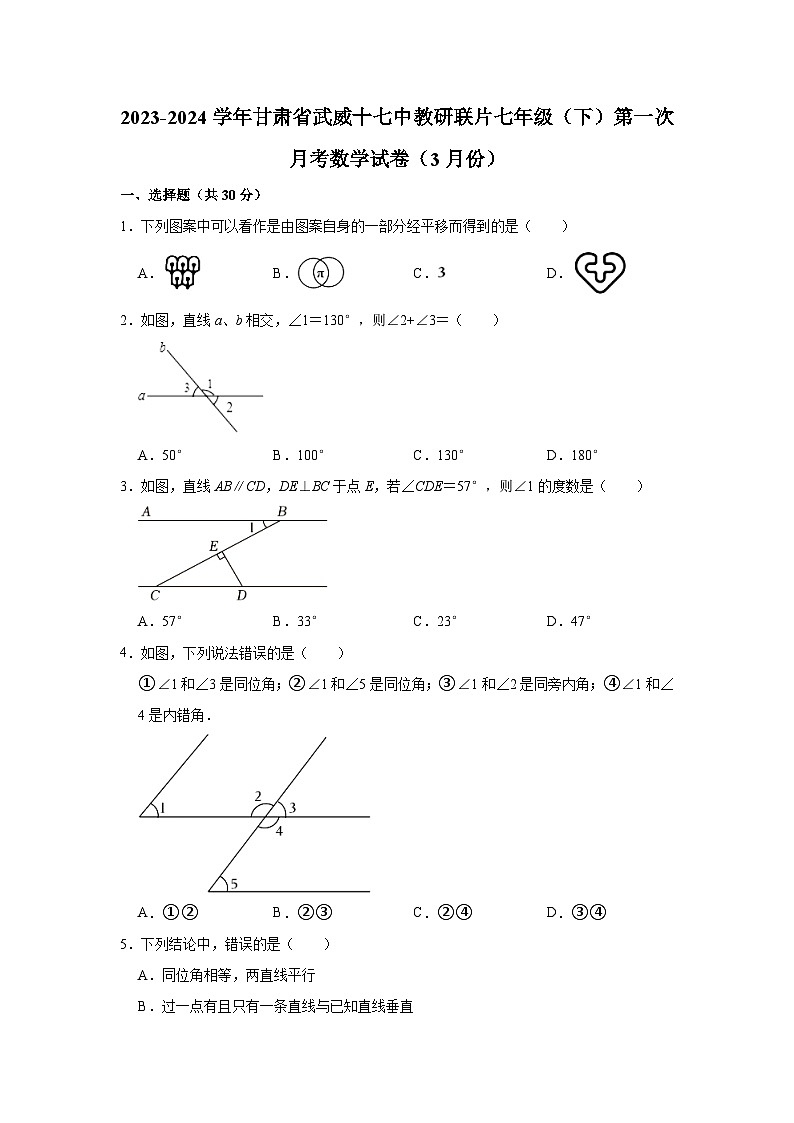
展开1.下列图案中可以看作是由图案自身的一部分经平移而得到的是( )
A.B.C.D.
2.如图,直线a、b相交,∠1=130°,则∠2+∠3=( )
A.50°B.100°C.130°D.180°
3.如图,直线AB∥CD,DE⊥BC于点E,若∠CDE=57°,则∠1的度数是( )
A.57°B.33°C.23°D.47°
4.如图,下列说法错误的是( )
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
A.①②B.②③C.②④D.③④
5.下列结论中,错误的是( )
A.同位角相等,两直线平行
B.过一点有且只有一条直线与已知直线垂直
C.同一平面内的两条直线不平行就相交
D.过一点有且只有一条直线与已知直线平行
6.如图,已知AB∥FE,∠ABC=75°,∠CDE=130°,则∠BCD的值为( )
A.80°B.40°C.30°D.25°
7.按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A.B.C.2D.3
8.下列各式中正确的是( )
A.B.C.D.
9.下列说法错误的是( )
A.﹣1的立方根是﹣1
B.算术平方根等于本身的数是±1,0
C.
D.3的平方根是±
10.有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1B.2C.3D.4
二、填空题(共24分)
11.的平方根是 ,﹣64的立方根是 .
12.比较大小: .
13.如果的平方根是±3,则= .
14.如图,在用数字标注的角中,∠4与 是同位角,与 是内错角,与 是同旁内角.
15.如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是 °.
16.如图,l1∥l2,直线AB截l1于点A,截l2于点B,BC⊥AB,若∠1=30°,则∠2= .
17.如图,AB∥CD,射线FE,FG分别与AB,CD交于点M,N,若∠F=∠FND=3∠EMB,则∠F的度数是 .
18.如图,若使得AB∥DC,则可以添加的一个条件是 .
三、计算和化简(共8分)
19.计算和化简:
(1);
(2)(﹣2x2)3+x2•x4﹣(﹣3x3)2.
四、解答题(共58分)
20.已知正数x的两个不同的平方根是2a+3和1﹣3a,y的立方根是﹣3,求x+y的值.
21.表示实数a,b的点在数轴上的位置如图所示,化简代数式的值.
22.已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是的整数部分,求a+2b+c的算术平方根.
23.如图,已知AB∥CD,∠4=3∠3,∠2=80°,求∠1的度数.
24.如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.求证:AC∥DF.
25.如图,已知∠1=∠3,∠2+∠3=180°,则AB∥DE.完成下面的说理过程(填空).
解:将∠2的邻补角记作∠4,则
∠2+∠4= ° .
又∵∠2+∠3=180°,
∴∠3=∠4 .
又∵∠1=∠3,
∴ = (等量代换),
∴AB∥DE .
26.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
27.将直角三角板OMN的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图,若∠BON=60°,求∠AOM的度数;
(2)若∠AOM=2∠COM,求∠AON的度数;
(3)将直角三角板OMN绕顶点O按逆时针方向旋转,在旋转过程中:当∠BON=120°时,求∠COM的度数.
参考答案
一、选择题(共30分)
1.下列图案中可以看作是由图案自身的一部分经平移而得到的是( )
A.B.C.D.
【分析】根据平移不改变图形的形状和大小,结合图案,对选项一一分析,排除错误答案.
解:观察图形可知;图案A是自身的一部分沿着直线运动而得到,是平移得到的;
故选:A.
【点评】本题考查了利用平移设计图案,图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.
2.如图,直线a、b相交,∠1=130°,则∠2+∠3=( )
A.50°B.100°C.130°D.180°
【分析】根据图形及∠1=130°可求出∠2和∠3的值,进而能得出∠2+∠3的值.
解:由图形可得:∠2=∠3=180°﹣∠1=50°,
∴∠2+∠3=100°.
故选:B.
【点评】本题考查了邻补角和对顶角的知识,比较简单,注意在计算角度时不要出错.
3.如图,直线AB∥CD,DE⊥BC于点E,若∠CDE=57°,则∠1的度数是( )
A.57°B.33°C.23°D.47°
【分析】根据直角三角形的两锐角互余得出∠DCE=33°,根据平行线的性质即可求解.
解:∵DE⊥BC,∠CDE=57°,
∴∠DCE=90°﹣∠CDE=90°﹣57°=33°,
∵AB∥CD,
∴∠1=∠ECD=33°,
故选:B.
【点评】本题考查了直角三角形的两锐角互余,平行线的性质,熟练掌握平行线的性质是解题的关键.
4.如图,下列说法错误的是( )
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
A.①②B.②③C.②④D.③④
【分析】根据同位角、同旁内角、内错角的定义判断.
解:①∠1和∠3是同位角是正确的;
②∠1和∠5不是同位角,原来的说法错误;
③∠1和∠2是同旁内角是正确的;
④∠1和∠4不是内错角,原来的说法错误.
故选:C.
【点评】本题考查了同位角、内错角、同旁内角,正确且熟练掌握同位角、内错角、同旁内角的定义和形状是解题的关键.
5.下列结论中,错误的是( )
A.同位角相等,两直线平行
B.过一点有且只有一条直线与已知直线垂直
C.同一平面内的两条直线不平行就相交
D.过一点有且只有一条直线与已知直线平行
【分析】根据平行线的性质与判定,平行公理,依次判断,即可求解.
解:A、同位角相等,两直线平行,正确,不符合题意,
B、过一点有且只有一条直线与已知直线垂直,正确,不符合题意,
C、同一平面内的两条直线不平行就相交,正确,不符合题意,
D、过直线外一点有且只有一条直线与已知直线平行,错误,符合题意,
故选:D.
【点评】本题考查了,平行线的性质与判定,平行公理,解题的关键是:熟练掌握相关定理.
6.如图,已知AB∥FE,∠ABC=75°,∠CDE=130°,则∠BCD的值为( )
A.80°B.40°C.30°D.25°
【分析】根据平行线的性质求出∠BFD的度数,由补角的定义求出∠CFD的度数,根据三角形外角的性质即可得出结论.
解:∵AB∥FE,
∴∠BFD=∠ABC=75°,
∴∠CFD=180°﹣∠BFD=105°,
又∵∠CDE=∠CFD+∠BCD,
∴∠BCD=∠CDE﹣∠CFD=130°﹣105°=25°.
故选:D.
【点评】本题考查的是平行线的性质,熟练掌握平行线的性质是解题关键.
7.按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A.B.C.2D.3
【分析】根据所给出的程序列出代数式,由实数混合运算的法则进行计算即可.
解:由所给的程序可知,当输入64时,=8,
∵8是有理数,
∴取其立方根可得到,=2,
∵2是有理数,
∴取其算术平方根可得到,
∵是无理数,
∴y=.
故选:A.
【点评】本题考查的是实数的运算,熟知有理数与无理数的概念是解答此题的关键.
8.下列各式中正确的是( )
A.B.C.D.
【分析】逐个判断各个选项,即可进行解答.
解:A、,故A不正确,不符合题意;
B、∵﹣4<0,∴无意义,故B不符合题意;
C、,故C正确,符合题意;
D、,故D不正确,不符合题意;
故选:C.
【点评】本题主要考查了算术平方根和立方根,解题的关键是掌握算术平方根和立方根的计算方法,以及算术平方根的被开方数不能为负数.
9.下列说法错误的是( )
A.﹣1的立方根是﹣1
B.算术平方根等于本身的数是±1,0
C.
D.3的平方根是±
【分析】根据算术平方根、平方根和立方根的概念判断即可.
解:A、﹣1的立方根是﹣1,说法正确,不符合题意;
A、算术平方根等于本身的数是1,0,原说法错误,符合题意;
C、=0.3,说法正确,不符合题意;
D、3的平方根是±,说法正确,不符合题意.
故选:B.
【点评】本题主要考查了算术平方根、平方根和立方根的概念,掌握其概念是解决此题的关键.
10.有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1B.2C.3D.4
【分析】利用对顶角的性质、两直线的位置关系、无理数的分类等知识分别判断后即可确定正确的选项.
解:①相等的角不一定是对顶角,原说法不正确,故不符合题意;
②两条平行线被第三条直线所截,同位角相等,故不符合题意;
③无理数包括正无理数、负无理数,0是有理数,故不符合题意;
④同一平面内,垂直于同一条直线的两条直线平行,所以命题正确;
所以真命题有1个;
故选:A.
【点评】此题主要考查了命题与定理,正确把握相关性质和定义是解题关键.
二、填空题(共24分)
11.的平方根是 ,﹣64的立方根是 ﹣4 .
【分析】根据算术平方根、平方根、立方根的定义解决此题.
解:∵,
∴的平方根是.
﹣64的立方根是﹣4.
故答案为:,﹣4.
【点评】本题主要考查算术平方根、平方根、立方根,熟练掌握算术平方根、平方根、立方根的定义是解决本题的关键.
12.比较大小: > .
【分析】利用作差法比较两个数的大小.
解:∵1<3<4,
∴1<<2,
∴﹣1>0,
∴﹣=>0,
∴>.
故答案为:>.
【点评】本题考查了实数大小的比较,此题的难点是利用“夹逼法”推知的取值范围.
13.如果的平方根是±3,则= 4 .
【分析】由平方根的定义可知=(±3)2,据此可得到a的值;将a的值代入,结合立方根的定义即可解答.
解:∵的平方根是±3,
∴=(±3)2=9,
∴a=81,
将a=81代入中,可得
=
=4.
故答案为:4.
【点评】本题考查算术平方根和平方根,掌握算术平方根和平方根的定义是解题的关键.
14.如图,在用数字标注的角中,∠4与 ∠1 是同位角,与 ∠2 是内错角,与 ∠3和∠5 是同旁内角.
【分析】根据同位角,内错角,同旁内角的定义,即可求解,
解:根据同位角,内错角,同旁内角的定义可得,
∠4与∠1是同位角,
∠4与∠1是内错角,
∠4与∠3 和∠5是同旁内角,
故答案为:∠1;∠2;∠3 和∠5.
【点评】本题考查了同位角,内错角,同旁内角的定义,解题的关键是:分清截线和被截线.
15.如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是 50 °.
【分析】根据对顶角相等可得∠BOD=∠AOC=75°,再根据角的和差关系求解.
解:∵∠AOC=75°,
∴∠BOD=∠AOC=75°,
∵∠1=25°,
∴∠2=∠BOD﹣∠1=75°﹣25°=50°,
故答案为:50.
【点评】本题考查对顶角的性质和角的和差关系,解题的关键是根据对顶角相等求出∠BOD的度数.
16.如图,l1∥l2,直线AB截l1于点A,截l2于点B,BC⊥AB,若∠1=30°,则∠2= 60° .
【分析】根据垂直的定义,平角的定义可求∠3,再根据两直线平行,同位角相等求出∠2.
解:如图.
∵BC⊥AB,
∴∠ABC=90°,
∵∠1=30°,
∴∠3=180°﹣∠ABC﹣∠1=60°.
∵l1∥l2,
∴∠2=∠3=60°.
故答案为:60°.
【点评】本题考查了平行线的性质,垂直的定义,平角的定义,是基础题,熟记性质是解题的关键.
17.如图,AB∥CD,射线FE,FG分别与AB,CD交于点M,N,若∠F=∠FND=3∠EMB,则∠F的度数是 108° .
【分析】过点F作FH∥AB,根据平行线的判定与性质求解即可.
解:如图,过点F作FH∥AB,
∵AB∥CD,
∴AB∥FH∥CD,
∴∠EMB=∠EFH,∠HFN+∠FND=180°,
∵∠EFN=∠FND=3∠EMB,
∴∠EFH=∠EFN,
∴∠HFN=∠EFN,
∴∠EFN+∠EFN=180°,
∴∠EFN=108°,
故答案为:108°.
【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
18.如图,若使得AB∥DC,则可以添加的一个条件是 ∠2=∠4(答案不唯一) .
【分析】由平行线的判定,即可得到答案.
解:若使得AB∥DC,由内错角相等,两直线平行,可以添加的一个条件是∠2=∠4(答案不唯一)
故答案为:∠2=∠4(答案不唯一).
【点评】本题考查平行线的判定,关键是掌握平行线的判定方法.
三、计算和化简(共8分)
19.计算和化简:
(1);
(2)(﹣2x2)3+x2•x4﹣(﹣3x3)2.
【分析】(1)先将乘方,0次幂,负整数幂化简,再进行计算即可;
(2)先根据幂的运算法则,将各项化简,再合并同类项即可.
解:(1)原式=﹣4+1﹣2
=﹣5;
(2)原式=﹣8x6+x6﹣9x6
=﹣16x6.
【点评】本题主要考查了实数的混合运算,幂的运算法则,合并同类项,解题的关键是掌握相关运算法则,以及同底数幂相乘(除),底数不变,指数相加(减);幂的乘方,底数不变,指数相乘;积的乘方,把每个因式分别乘方;合并同类项,字母和相同字母是指数不变,只把系数相加减.
四、解答题(共58分)
20.已知正数x的两个不同的平方根是2a+3和1﹣3a,y的立方根是﹣3,求x+y的值.
【分析】根据一个正数有两个平方根,它们互为相反数得出方程,求出a,即可求出x、y,代入x+y求出即可.
解:∵正数x的两个平方根分别是2a+3和1﹣3a,
∴2a+3+1﹣3a=0,
a=4,
∴x=(2×4+3)2=121,
∵y的立方根是﹣3,
∴y=(﹣3)3=﹣27,
∴x+y=121﹣27=94.
【点评】本题考查了平方根,立方根的应用,注意:一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根.
21.表示实数a,b的点在数轴上的位置如图所示,化简代数式的值.
【分析】直接利用绝对值的性质以及二次根式的性质、立方根的性质分别化简,进而得出答案.
解:由数轴可得:﹣1<b<0,1<a<2,
则1﹣a<0,b+1>0,a﹣2<0,
故原式=a﹣1+2﹣a﹣(b+1)+b
=a﹣1+2﹣a﹣b﹣1+b
=0.
【点评】此题主要考查了实数的运算,正确得出各式的符号是解题关键.
22.已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是的整数部分,求a+2b+c的算术平方根.
【分析】先根据平方根与立方根的概念可得2a﹣1与3a+b﹣9的值,估计的值,从而求出a+2b+c的值,最后求算术平方根即可.
解:∵2a﹣1的平方根是±3,
∴2a﹣1=9,2a=10,a=5,
∵3a+b﹣9的立方根是2,
∴3a+b﹣9=8,15+b﹣9=8,b=2,
∵,
∴c=﹣7,
∴a+2b+c=5+4﹣7=2,
∴a+2b+c的算术平方根为.
故答案为:.
【点评】此题考查了算术平方根、平方根、立方根的定义及求解,无理数的估算与整数部分的求解,解题的关键是二次根式的基本运算.
23.如图,已知AB∥CD,∠4=3∠3,∠2=80°,求∠1的度数.
【分析】根据两直线平行,同位角相等,结合∠4=3∠3,∠2=80°,求出∠3=20°,根据三角形外角定理得到∠2=∠3+∠5,即可求解,
解:如图,
∵AB∥CD,∠4=3∠3,
∴∠2=∠4+∠3=4∠3=80°,
∴∠3=20°,
∵∠2=∠3+∠5,
∴∠5=∠2﹣∠3=60°,
∴∠1=∠5=60°,
故答案为:∠1=60°.
【点评】本题考查了平行线的性质,三角形外角定理,解题的关键是:熟练掌握相关性质定理.
24.如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠C=∠D.求证:AC∥DF.
【分析】先由对顶角相等,得到:∠1=∠DMF,然后根据等量代换得到:∠2=∠DMF,然后根据同位角相等两直线平行,得到BD∥CE,然后根据两直线平行,同位角相等,得到∠C=∠DBA,然后根据等量代换得到:∠D=∠DBA,最后根据内错角相等两直线平行,即可得到DF与AC平行.
【解答】证明:∵∠1=∠DMF,∠1=∠2,
∴∠2=∠DMF,
∴BD∥CE,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠D=∠DBA,
∴AC∥DF.
【点评】本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.
25.如图,已知∠1=∠3,∠2+∠3=180°,则AB∥DE.完成下面的说理过程(填空).
解:将∠2的邻补角记作∠4,则
∠2+∠4= 180 ° 平角的定义 .
又∵∠2+∠3=180°,
∴∠3=∠4 同角的补角相等 .
又∵∠1=∠3,
∴ ∠1 = ∠4 (等量代换),
∴AB∥DE 同位角相等,两直线平行 .
【分析】证明∠1=∠4,根据平行线的判定解答即可.
解:由对顶角的性质得∠2+∠4=180°(平角的定义).
∠3=∠4(同角的补角相等).
∠1=∠4,
AB∥DE(同位角相等,两直线平行).
故答案为:180;平角的定义;同角的补角相等;∠1,∠4;同位角相等,两直线平行.
【点评】此题考查平行线的判定,关键是根据平行线的判定解答.
26.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
【分析】(1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;
(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.
解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
【点评】本题考查了平行线的性质,对顶角相等的性质,垂线的定义,(2)根据度数相等得到相等的角是关键.
27.将直角三角板OMN的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图,若∠BON=60°,求∠AOM的度数;
(2)若∠AOM=2∠COM,求∠AON的度数;
(3)将直角三角板OMN绕顶点O按逆时针方向旋转,在旋转过程中:当∠BON=120°时,求∠COM的度数.
【分析】(1)由已知条件:∠BON=60°,根据邻补角的定义可得出∠AON的度数,根据角平分线定义可得∠CON的度数,由∠MON=90°,即可得出答案;
(2)设∠COM=x°,用x表示出∠CON,再根据∠CON=90°列出方程求得x,进而求得∠AON;
(3)分两种情况:当ON在直线AB上方时,当ON在直线AB下方时,分别求出结果便可.
解:(1)∵∠BON=60°,∠MON=90°,
∴∠AOM=180°﹣60°﹣90°=30°,
(2)∵OC平分∠AON,
∴∠AOC=∠CON,
又∵∠AOM=2∠COM,
设∠COM=x,
∴∠AOM=2x,
∴∠CON=∠AOC=3x,
∵∠COM+∠CON=90°,
∴x+3x=90°,
解得x=22.5°,
∴∠AON=6x=135°;
(3)当ON在直线AB上方时,
∵∠BON=120°,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=30°,
∵∠MON=90°,
∴∠COM=60°,
当ON在直线AB下方时,
∵∠BON=120°,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=30°,
∵∠MON=90°,
∴∠COM=120°,
综上所述:∠COM的度数为60°或120°.
【点评】本题主要考查了角平分线的定义及角的计算,熟练掌握角平分线的定义及角的计算的方法进行求解是解决本题的关键.
甘肃省武威市凉州区武威第二十四中学教研联片2023-2024学年七年级下学期3月月考数学试题(原卷版+解析版): 这是一份甘肃省武威市凉州区武威第二十四中学教研联片2023-2024学年七年级下学期3月月考数学试题(原卷版+解析版),文件包含甘肃省武威市凉州区武威第二十四中学教研联片2023-2024学年七年级下学期3月月考数学试题原卷版docx、甘肃省武威市凉州区武威第二十四中学教研联片2023-2024学年七年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
2024年甘肃省武威市凉州区武威第七中学教研联片中考第一次模拟诊断数学模拟预测题(原卷版+解析版): 这是一份2024年甘肃省武威市凉州区武威第七中学教研联片中考第一次模拟诊断数学模拟预测题(原卷版+解析版),文件包含2024年甘肃省武威市凉州区武威第七中学教研联片中考第一次模拟诊断数学模拟预测题原卷版docx、2024年甘肃省武威市凉州区武威第七中学教研联片中考第一次模拟诊断数学模拟预测题解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
2024年甘肃省武威十一中教研联片九年级中考数学一模试卷+: 这是一份2024年甘肃省武威十一中教研联片九年级中考数学一模试卷+,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












