人教版九年级数学上册同步精品课堂 24.2.2 直线和圆的位置关系（课件）

这是一份人教版九年级数学上册同步精品课堂 24.2.2 直线和圆的位置关系（课件），共23页。

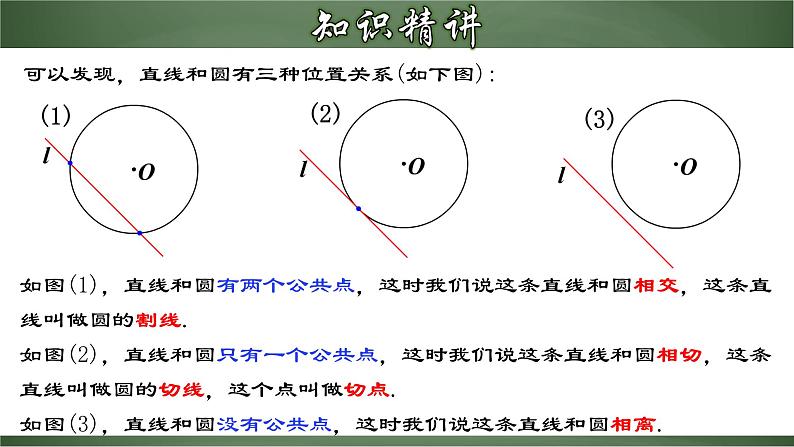
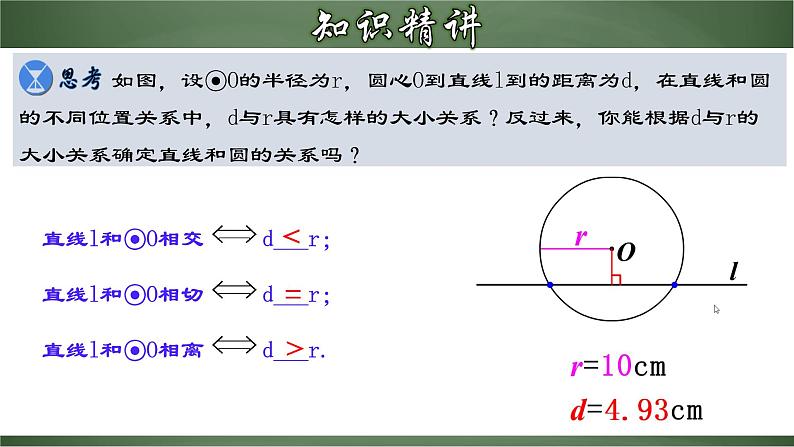
直线和圆的位置关系1.了解直线和圆的位置关系.2.了解直线与圆的不同位置关系时的有关概念.3.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的 数量关系.(重点）4.会运用直线和圆的三种位置关系的性质与判定进行有关计算.(难点）设⊙O的半径为r，点P到圆心的距离OP=d，d＞rd＝rd＜r1.若⊙O的直径为12cm，OD=8cm，则点D在⊙O____.2.如图，点B在直线AC上，且OA⊥AC，则OA＜___＜___，点O到直线AC的距离即为线段___的长.外OBOCOA 在太阳升起的过程中，太阳和海平线会有几种位置关系？如果我们把太阳看作一个圆，把海平线看作一条直线，由此你能得出直线和圆的位置关系吗？ 作一个圆，把直尺的边缘看成一条直线.固定圆，平移直尺，观察直线和圆有几种位置关系？他们的交点个数如何变化？可以发现，直线和圆有三种位置关系(如下图):如图(1)，直线和圆有两个公共点，这时我们说这条直线和圆相交，这条直线叫做圆的割线.如图(2)，直线和圆只有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点.如图(3)，直线和圆没有公共点，这时我们说这条直线和圆相离. 如图，设⊙O的半径为r，圆心O到直线l到的距离为d，在直线和圆的不同位置关系中，d与r具有怎样的大小关系？反过来，你能根据d与r的大小关系确定直线和圆的关系吗？＞＜=     例2.在平面直角坐标系中，圆心O的坐标为(-3，4)，以半径r在坐标平面内作圆，（1）当r 时，圆O与坐标轴有1个交点；（2）当r 时，圆O与坐标轴有2个交点；（3）当r 时，圆O与坐标轴有3个交点；（4）当r 时，圆O与坐标轴有4个交点； 例3.如图，P为正比例函数y=1.5x图象上的一个动点，☉P的半径为3，设点P的坐标为(x，y).(1)求OP与直线x=2相切时点P的坐标;(2)请直接写出☉P与直线x=2相交、相离时x的取值范围.解:(1)如图，过点P作直线x=2的垂线，垂足为A.当点P在直线x=2左侧时，PA=2-x=3，得x=-1∴P(-1，-1.5)当点P在直线x=2右侧时,AP=x-2=3，得x=5∴P(5，7.5)例3.如图，P为正比例函数y=1.5x图象上的一个动点，☉P的半径为3，设点P的坐标为(x，y).(1)求OP与直线x=2相切时点P的坐标;(2)请直接写出☉P与直线x=2相交、相离时x的取值范围.解:(2)当-15时， ☉P与直线x=2相离.1.☉O的半径是6，点O到直线l的距离为5，则直线l与☉O的位置关系为( )A.相离 B.相切 C.相交 D.无法确定2.已知☉O的半径是5，直线l是☉O的切线，则点O到直线l的距离是( )A.2.5 B.3 C.5 D.103.设☉O半径为3，点O到直线l的距离为d，若直线l与☉O没有公共点，则d应满足的条件是( )A.d<3 B.d>3 C.d≥3 D.d≤3CCB4.☉O的半径为2cm，直线l上有一点P，且PO=2cm，则☉O与l的位置关系是( )A.相离 B.相离或相切 C.相切 D.相切或相交5.在平面直角坐标系中,以点(-3，4)为圆心，4为半径的圆( )A.与x轴相交，与y轴相切 B.与x轴相离，与y轴相交C.与x轴相切，与y轴相交 D.与x轴相切，与y轴相离DC6.如图(1)，已知∠AOB=30°，P为0B上一点，且OP=5cm，以点P为圆心，以r=2.5cm为半径的圆和直线OA的位置关系是_____;以r=2cm为半径的圆和直线0A的位置关系是______;以r=4cm为半径的圆和直线OA的位置关系是______.7.如图(2)，两个同心圆，大圆的半径为5cm，小圆的半径为3cm,若大圆的弦AB与小圆相交，则弦AB的取值范围是____________.相切相离相交8＜AB≤108.如图，在平面直角坐标系中有一矩形OABC，点B的坐标为(4，2)，现有一圆同时和这个矩形的三边都相切(切点都在矩形的边上)，则此圆的圆心D的坐标为___________________________.(1,1)或(3,1)或(2,0)或(2,2)9.圆的直径是13cm，如果圆心与直线的距离分别是：(1) 4.5cm； (2) 6.5cm； (3) 8cm，那么直线和圆分别是什么位置关系？有几个公共点？解：∵ 圆的直径是13cm，∴ 圆的半径是6.5cm(1)∵ 4.5cm＜6.5cm，∴ 直线和圆相交，有两个公共点；(2)∵ 6.5cm＝6.5cm，∴ 直线和圆相切，只有一个公共点；(3)∵ 8cm＞6.5cm，∴ 直线和圆相离，没有公共点.10.如图，Rt△ABC，∠ACB=90°，AB=8cm,AC=4cm，CD⊥AB.(1)以点C为圆心作圆，当半径为多长时，直线AB和OC相切?(2)以点C为圆心，分别以2cm和4cm的长为半径作两个圆，直线AB和这两个圆分别有怎样的位置关系. 10.如图，Rt△ABC，∠ACB=90°，AB=8cm,AC=4cm，CD⊥AB.(1)以点C为圆心作圆，当半径为多长时，直线AB和OC相切?(2)以点C为圆心，分别以2cm和4cm的长为半径作两个圆，直线AB和这两个圆分别有怎样的位置关系. 小结梳理