2024年河南省驻马店市一模数学模拟试题（含解析）

这是一份2024年河南省驻马店市一模数学模拟试题（含解析），共21页。试卷主要包含了填空题，解答题，八年级抽取的学生测试成绩统计表等内容，欢迎下载使用。

1．下列各数中，比小的数是（ ）
A．B．C．D．0
2．杆秤是中国最古老也是现今人们仍然使用的衡量工具，由秤杆、秤砣、秤盘三个部分组成.秤砣、秤杆分别叫做“权”和“衡”，指的是做任何事都要权衡轻重.如图是常见的一种秤砣，则它的主视图是（ ）
A． B． C． D．
3．芯片制造过程中，需要在芯片表面上沉积各种薄膜层，如金属、绝缘体和半导体. 单位“埃”被用来描述薄膜的厚度，符号为“”.已知，即纳米的十分之一. 若将“”用科学记数法表示，则（ ）
A．8B．C．9D．
4．下列等式，成立的是（ ）
A．B．
C．D．
5．在“三角尺拼角”实验中，小聪把一副三角尺按如图所示的方式放置，则的度数为（ ）
A．B．C．°D．
6．若关于x的方程有两个不相等的实数根，则m的值可以是（ ）
A．0B．C．D．
7．如图，是半圆O的直径，C、D是半圆弧上两点，若，则的度数为（ ）

A．138°B．148°C．132°D．122°
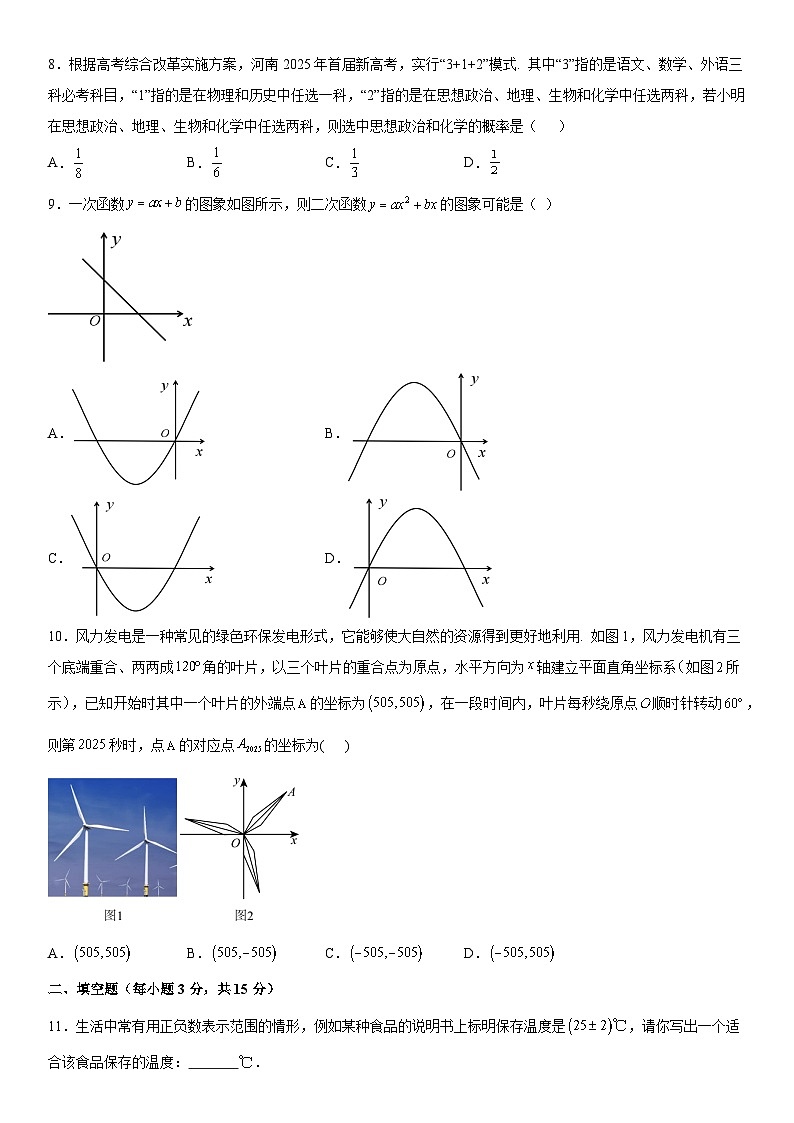
8．根据高考综合改革实施方案，河南2025年首届新高考，实行“3+1+2”模式. 其中“3”指的是语文、数学、外语三科必考科目，“1”指的是在物理和历史中任选一科，“2”指的是在思想政治、地理、生物和化学中任选两科，若小明在思想政治、地理、生物和化学中任选两科，则选中思想政治和化学的概率是（ ）
A．B．C．D．
9．一次函数的图象如图所示，则二次函数的图象可能是（ ）
A．B．
C．D．
10．风力发电是一种常见的绿色环保发电形式，它能够使大自然的资源得到更好地利用. 如图1，风力发电机有三个底端重合、两两成角的叶片，以三个叶片的重合点为原点，水平方向为轴建立平面直角坐标系如图所示，已知开始时其中一个叶片的外端点的坐标为，在一段时间内，叶片每秒绕原点顺时针转动，则第秒时，点的对应点的坐标为( )
A．B．C．D．
二、填空题（每小题3分，共15分）
11．生活中常有用正负数表示范围的情形，例如某种食品的说明书上标明保存温度是，请你写出一个适合该食品保存的温度： ．
12．若点在第二象限，则m的取值范围是 ．
13．香港国际六人板球赛（Hng Kng Internmtinml Cricket Sixes），是国际板球赛一大盛事. 在一次比赛中，甲、乙两支板球队队员的身高统计如图所示，则参加比赛的甲、乙两队队员的身高更整齐的是 队．（填“甲”或“乙”）
14．如图，平行四边形的对角线、交于点O，且，以O为圆心，分别以、的长为半径画弧交对角线于点E、F，若，，则图中阴影部分的面积为 ．
15．如图，正方形中，为边的中点，连接为边AD上一动点，将沿所在直线翻折，若点A的对应点恰好落在的边上，则线段的长为 ．
三、解答题（本大题共8个小题，共75分）
16．（1）计算：；
（2）化简：．
17．豫剧，是中国五大戏曲剧种之一、中国第一大地方剧种，是主要流行于河南省、河北、山东，传承已有上百年的历史，被西方人称赞是“东方咏叹调”、“中国歌剧”等．某校为了解七、八年级学生对豫剧文化的了解程度，组织了一次豫剧文化知识测试，七、八年级各抽取10名学生参加比赛，现对测试成绩（百分制）进行整理、描述和分析（成绩用x（分）表示），共分成四个等级（A：，B：，C：，D：）.下面给出了部分信息：

七年级参赛的学生等级的成绩为：、、、
八年级参赛的学生等级的成绩为：、、、、
七、八年级抽取的学生测试成绩统计表：
请根据相关信息，回答以下问题：
(1)填空： ， ；
(2)七年级参赛学生成绩扇形图中等级的圆心角度数是 ；
(3)在这次测试中，七年级学生小明与八年级学生小亮的成绩都是分，于是小明说：“我在七年级参赛小队的名次高于小亮在八年级参赛小队的名次.”你同意小明的说法吗？并说明理由．
18．如图，在中，，点D在上，且，连接．
(1)请用无刻度的直尺和圆规过点A作的垂线（保留作图痕迹，不写作法）；
(2)若（1）中所作的垂线交边于点E，连接． 求证：．
19．儿童放学归来早，忙趁东风放纸鸢． 某数学兴趣小组周末到空旷的草地上放风筝，并利用所学知识测量风筝的高度． 如图，在处用测角仪测得风筝的仰角为，保持风筝不动，沿方向前进到达处，又测得风筝的仰角为． 已知测角仪的高度为． 求风筝的高度（结果精确到． 参考数据：，，）
20．如图，在平面直角坐标系中，直线与双曲线交于A、B两点，其中A的坐标为，D是以点为圆心，半径长为1的圆上一动点，连接，E为的中点.
(1)求直线和双曲线的解析式；
(2)求线段长度的最小值．
21．围棋起源于中国，古代称为“弈”，是棋类鼻祖，围棋距今已有四千多年的历史. 中国象棋也是中华民族的文化瑰宝，它源远流长，趣味浓厚，基本规则简明易懂.国家“双减”政策实施后，某校为参加社团的同学去商场购买中国象棋和围棋. 其中购买40副象棋和20副围棋共花费2600元，已知购买1副象棋比1副围棋少花10元.
(1)求每副象棋和围棋的单价；
(2)随着社团活动的开展和同学们对棋类运动的热爱，学校决定再次购买40副围棋和副中国象棋，在购买时，恰逢商场推出了优惠活动，活动的方案如下：
方案一：购买围棋超过20副时，超过部分每购买1副围棋赠送1副中国象棋；
方案二：按购买总金额的八折付款．
分别求出按照方案一、二购买的总费用、关于m的函数关系式；
(3)若选择方案二购买更合算，求m的取值范围．
22．某公园要在小广场上建造一个喷泉景观.在小广场中央处垂直于地面安装一个高为1.25米的花形柱子，安置于柱子顶端A处的喷水向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过的任一平面上抛物线路径如图1所示．为使水流形状较为美观，设计成水流在距的水平距离为1米时到达最大高度，此时离地面2.25米．

(1)以点为原点建立如图2所示的平面直角坐标系，水流到水平距离为米，水流喷出的高度为米，求出在第一象限内的抛物线解析式（不要求写出自变量的取值范围）；
(2)张师傅正在喷泉景观内维修设备期间，喷水管意外喷水，但是身高1.76米的张师傅却没有被水淋到，此时他离花形柱子的距离为米，则的取值范围是______________；
(3)在平面内，把一个图形上的任意一点与另一个图形上任意一点之间的距离的最小值称为这两个图形的距离．为了美观，在离花形柱子4米处的地面处安装射灯，射灯射出的光线与地面成角，如图3所示，光线交汇点在花形柱子的正上方，其中光线所在的直线解析式为，求光线与抛物线水流之间的距离．
23．综合与实践
综合与实践课上，老师让同学们以“两个相似矩形的平移”为主题探究线段之间的数量关系：如图，矩形与矩形相似，其中，，点E、F在直线上，且点C、D、G、H在直线的同侧，矩形沿直线左右平移，O为的中点，直线与直线相交于点P（点P、D不重合），直线与直线相交于点Q（点Q、C不重合），试探究与之间的数量关系．
【操作判断】
（1）如图1，平移矩形，当，点A、E重合时，线段与之间的数量关系是 ；
【迁移探究】
（2）继续平移矩形，对任意正数k，（1）中的判断是否都成立，请就图2的情形说明理由；
【拓展应用】
（3）如图3，若，，，平移矩形，连接交于点M，当是直角三角形时，请直接写出OA的长．
参考答案与解析
1．A
【分析】本题考查了有理数比较大小，根据有理数的比较大小法则，进行比较即可．
【解答】解：∵，，，
∴，，，
故选：A．
2．A
【分析】
本题考查了三视图，解题关键是掌握三视图的确定方法，根据从正面看到的图形确定即可．
【解答】解：这个常见的一种秤砣的主视图是
故选A．
3．D
【分析】
本题考查了科学记数法，解题关键是明确科学记数法的表示方法，正确确定指数．
【解答】解：，
写出科学记数法为，
故选：D．
4．B
【分析】
本题考查了整式的运算，解题关键是掌握整式运算法则，准确进行计算；
根据完全平方公式、平方差公式、幂的运算，因式分解判断即可．
【解答】解：A. ，原选项不符合题意；
B. ，原选项符合题意；
C. ，原选项不符合题意；
D. ，原选项不符合题意；
故选：B．
5．C
【分析】
本题考查了三角形的外角的性质，根据三角形的外角的性质，即可求解．
【解答】解：，
故选：C．
6．A
【分析】
本题考查了一元二次方程根的判别式，根据方程有两个不相等的实数根，求出m的取值范围即可．
【解答】解：∵关于x的方程有两个不相等的实数根，
∴，
解得，，
在选项中，只有0符合题意，
故选：A．
7．C
【分析】
本题考查了圆周角的性质和圆内接四边形的性质，熟记直径所对圆周角为直角和圆内接四边形对角互补是解题关键．
连接，根据圆心角的性质求出的度数，再根据圆内接四边形的性质求出的度数即可．
【解答】解：连接，
∵是半圆O的直径，
∴，
∵，
∴，
∴，
故选：C．

8．B
【分析】
本题考查的是树状图法求概率．画出树状图，共有12种等可能的结果，其中小明选中地理和化学的结果有2种，再由概率公式求解即可．
【解答】
解：把思想政治、地理、生物和化学分别记为、、、，
画树状图如下：
共有12种等可能的结果，其中小明选中地理和化学的结果有2种，
小明选中地理和化学的概率是，
故选：B．
9．D
【分析】根据一次函数图像经过的象限以及与坐标轴的交点可知：，由此可知二次函数开口方向，坐标轴情况，依此判断即可．
【解答】解：观察一次函数图像可知，
∴二次函数开口向下，
对称轴，
故选：D．
【点拨】本题主要考查一次函数的图像以及二次函数的图像，根据一次函数图像经过的象限以及与坐标轴的交点情况判断a、b的正负是解题的关键．
10．C
【分析】
本题考查了旋转的性质，点的坐标，根据叶片每秒绕原点顺时针转动，找到规律，进而得出第时，点A的对应点的坐标与相同，且与点关于原点对称，即可求得点的对应点的坐标．
【解答】解：∵，
∴A在第一象限的角平分线上，
∵叶片每秒绕原点顺时针转动，
∴点A的坐标以每6秒为一个周期依次循环，
∵，
∴第时，点A的对应点的坐标与相同，且与点关于原点对称，
为．
故选：C．
11．25（答案不唯一）．
【分析】
本题考查了正负数的意义，根据给出的范围写出符合题的温度即可．
【解答】因为某种食品的说明书上标明保存温度是，
所以适合该食品保存的温度可以是，
故答案为：25（答案不唯一）．
12．
【分析】
本题考查了点的坐标的特征，运用第二象限点的横坐标为负，纵坐标为正求解即可．
【解答】解：点在第二象限，
∴，
∴，
故答案为：．
13．甲
【分析】
本题考查折线统计图以及方差，关键是掌握方差的意义，根据波动情况进行判断．
【解答】解：看甲、乙两队队员的身高哪个更整齐，主要是看两组数据的波动大小，
根据折线统计图可知，甲队的波动小，乙队的波动大，
故答案为：甲．
14．
【分析】
本题考查扇形面积的计算、平行四边形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
根据三角函数可以得到的度数，然后根据图形可知阴影部分的面积的面积扇形的面积），再代入数据计算即可．
【解答】
解：∵平行四边形ABCD的对角线AC、BD交于点O，，，，
，，
，
，
图中阴影部分的面积为：
，
故答案为：．
15．1或
【分析】先画出满足条件的，进行分类当讨论：当A的对称点落在上时， 结合折叠
性质以及正切定义进行列式计算，当A的的对称点落在上时，即点；此时P为上的连接交于一点，结合折叠性质，得直线是的平分线，根据角平分线的性质，得，根据正切定义，进行列式计算，得，再证明，再根据对应边成比例列式，代入数值进行计算，即可作答．
【解答】解：如图：以点B为圆心，为直径画圆，与分别相交于两点，且为，然后过点B分别作的垂直平分线交于
当A的的对称点落在上时，即点；此时P为上的连接
∵四边形是正方形
∴
则
即
∴
∵为边的中点，
∴
故
∴
如图：
当A的的对称点落在上时，即点；此时P为上的连接交于一点，
∵沿所在直线翻折
∴
即直线是的平分线，过点G作，
∴
∵四边形是正方形
∴
∴
则
设，
则
∵
∴
则中，得
即
解得
∵
∴
则
解得
综上：线段的长为1或
故答案为：1或
【点拨】本题考查了正方形与折叠问题，勾股定理，三角函数的定义，相似三角形的判定与性质及角平分线的性质，难度较大，综合性强，正确掌握相关性质内容是解题的关键．
16．（1）0，（2）
【分析】
本题考查了实数的运算以及分式的混合运算．
（1）分别化简绝对值、零指数幂、负指数幂再进行合并即可．
（2）根据分式的运算法则即可求出答案．
【解答】解：（1）
（2）
17．(1)，
(2)
(3)同意小明的说法，见解析
【分析】
此题考查了条形统计图与扇形统计图；求中位数，众数，利用中位数做分析；
（1）利用八年级（一）的百分比求出组与组的人数，即可得到中位数的值；根据次数出现最多的数是众数得到的值；
（2）求得组的占比，乘以即可求解；
（3）利用中位数分析名次．
【解答】（1）解：八年级（一）中，组人数为，组人数为，
人中第、人的成绩分别为，，故中位数，
八年级（二）中成绩出现次数最多的是，故；
故答案为：，；
（2）组的占比为
∴七年级参赛学生成绩扇形图中D等级的圆心角度数是
故答案为：．
（3）∵八年级（一）班的中位数为分，（一）班学生小明的成绩是分，
他在（一）班中是前名，
而（二）班的中位数是分，学生小亮的成绩是分，
他在（二）班是后名，
∴同意小明的说法．
18．(1)见解析
(2)见解析
【分析】
本题考查了尺规作图和等腰三角形的性质，解题关键是熟练掌握尺规作图和等腰三角形的性质．
（1）分别以C、D为圆心，大于为半径作弧，经过A和两弧交点画直线即可；
（2）利用“三线合一”得出垂直平分，得出，再利用等腰三角形的性质即可得到结论．
【解答】（1）解：如图所示：是的垂线．
（2）证明：∵，是的垂线．
∴垂直平分，
∴，
∴，
∴
∴．
19．米
【分析】本题考查了解直角三角形的应用，延长交于点，则四边形是矩形，设，得出，在中，，求得的值，即可求解．
【解答】解：如图所示，延长交于点，则四边形是矩形，
依题意，，
设，
∵，
∴，
∴，
在中，
∴
解得：
∴风筝的高度为（米）．
20．(1)；
(2)2
【分析】
本题考查了求函数解析式、中位线和圆的有关知识，解题关键是熟练运用待定系数法求出解析式，利用中位线和三角形三边关系求出最小值．
（1）把代入解析式，用待定系数法求解即可，
（2）连接，根据反比例函数的性质和中位线确定的取值范围即可．
【解答】（1）解：把代入得，
，解得，直线解析式为；
把代入得，
，解得，反比例函数解析式为．
（2）解：连接，，，
∵直线与双曲线交于A、B两点，
∴，
∵E为的中点，
∴，
，，
∵，
∴最小值为4，
∴线段长度的最小值为2．
21．(1)每副象棋的价格是40元，每副围棋的价格是50元
(2)见解析
(3)
【分析】
本题考查了二元一次方程、一元一次不等式和列函数解析式，解题关键是准确把握题目中的数量关系，正确列出方程或不等式．
（1）设每副象棋的价格是元，每副围棋的价格是元，列出关于，的二元一次方程组，解之即可得出结论；
（2）根据题目给出的优惠方案，列出关系式即可；
（3）根据题意列出不等式求解即可．
【解答】（1）解：设每副象棋的价格是元，每副围棋的价格是元，
根据题意得：，
解得：．
答：每副象棋的价格是40元，每副围棋的价格是50元；
（2）解：根据购买围棋超过20副时，超过部分每购买1副围棋赠送1副中国象棋，
可得；
根据按购买总金额的八折付款，
可得．
（3）解：根据题意得，
，
解得，，
所以，m的取值范围．
22．(1)
(2)
(3)
【分析】（1）由题意得，在第一象限内的抛物线顶点的坐标，故设抛物线解析式为，将代入得，求值，进而可得在第一象限内的抛物线解析式；
（2）当时，，解得：，，由二次函数的图象与性质确定的取值范围即可；
（3）由题意知，，，设平行于直线且与抛物线只有一个交点的直线的解析式为，则联立方程，整理得，，令，解得，即直线的解析式为，如图，记直线与轴的交点为，则，则，根据光线与抛物线水流之间的最小垂直距离是直线到直线的距离，即为，计算求解即可．
【解答】（1）解：由题意得，在第一象限内的抛物线顶点的坐标，故设抛物线解析式为，
将代入得，
解得，，
在第一象限内的抛物线解析式为；
（2）解：当时，，
解得：，，
的取值范围是；
故答案为：．
（3）解：∵直线的解析式为：，
∴把代入得：，
把代入得：，解得：，
∴，，
∴，，
设平行于直线且与抛物线只有一个交点的直线的解析式为，
联立，即，
整理得：，
令，
解得，
∴直线的解析式为，
如图，设直线与轴的交点为，
把代入得：，
解得：，
则，

∴，
∵，
∴直线到直线的距离为，
根据题意得：光线与抛物线水流之间的距离为光线与抛物线水流之间的最小垂直距离，即直线到直线的距离，
∴光线与抛物线水流之间的距离为．
【点拨】本题主要考查了二次函数的应用，二次函数解析式，二次函数的图象与性质，二次函数综合，解直角三角形等知识．解题的关键在于对知识的熟练掌握与灵活运用．
23．（1）相等，（2）成立，见解析；（3）或
【分析】
（1）设根据中点列出比例式，表示出与的长度即可,
（2）设根据相似列出比例式，表示出与的长度即可,
（3）证，得出，再根据是直角三角形，分类讨论，利用相似三角形的性质求解即可．
【解答】解：（1）设则
∵O为的中点，
∴
∴，
∴，
，，
∴，
故答案为：相等；
（2）成立．
设则
∵O为的中点，
∴，
∵，
∴，
∴，
则，
同理，
设，则，，
∵，
∴
，
∴；
（3）∵，，，
∴，，，
由（2）得，
∵，，
∴，
∴，
如图，当时，
∵，，
∴，
∵，
∴，
∴，
则，
解得，或（舍去）
如图，当时，
同理可得，
∴，
则，
解得，或（舍去），
，
综上，或．
【点拨】本题考查了相似三角形的判定与性质、全等三角形的判定与性质，解题关键是准确证明三角形相似，利用相似三角形的性质进行推理证明．
班级
平均分
中位数
众数
七年级
八年级