2024年河南省驻马店市遂平县中考一模数学模拟试题

这是一份2024年河南省驻马店市遂平县中考一模数学模拟试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

数学（一）
注意：本试卷分试题卷和答题卡两部分，考试时间100分钟，满分120分．考生应首先阅读试题卷上的文字信息，然后在答题卡上作答，在试题卷上作答无效，交卷时只交答题卡．
一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的．）
1．下列各数中，最大的数是（ ）
A．－1B．－2C．2D．0
2．备受瞩目的《齐歌龍咚锵——2024河南春晚》拉满了喜庆的新年气氛，让河南卫视再次出圈．截止到2月8日中午12点，全网热搜阅读量超120亿．数据120亿用科学记数法表示为（ ）
A．B．C．D．
3．如图所示是一个正方体切去一角之后的剩余部分，其俯视图是（ ）
A．B．C．D．
4．计算的结果是（ ）
A．B．C．D．
5．如图所示，已知线段AB，观察作图痕迹，所得结论不一定成立的是（ ）
第5题图
A．B．C．D．
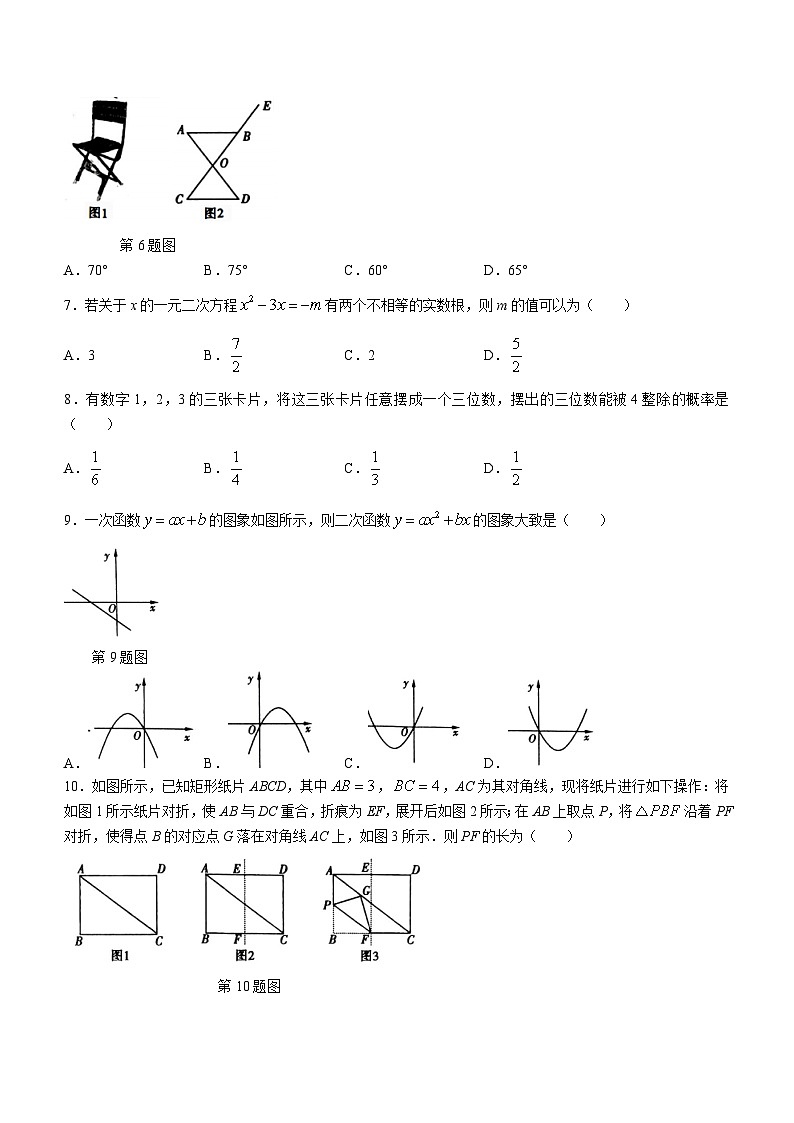
6．如图1所示为“钓鱼神器”马扎，图2为抽象出的几何模型，若，，，则（ ）
第6题图
A．70°B．75°C．60°D．65°
7．若关于x的一元二次方程有两个不相等的实数根，则m的值可以为（ ）
A．3B．C．2D．
8．有数字1，2，3的三张卡片，将这三张卡片任意摆成一个三位数，摆出的三位数能被4整除的概率是（ ）
A．B．C．D．
9．一次函数的图象如图所示，则二次函数的图象大致是（ ）
第9题图
A．B．C．D．
10．如图所示，已知矩形纸片ABCD，其中，，AC为其对角线，现将纸片进行如下操作：将如图1所示纸片对折，使AB与DC重合，折痕为EF，展开后如图2所示；在AB上取点P，将沿着PF对折，使得点B的对应点G落在对角线AC上，如图3所示．则PF的长为（ ）
第10题图
A．B．C．D．
二、填空题（每小题3分，共15分）
11．若式子在实数范围内有意义，则x的取值范围为______．
12．已知二元一次方程组，则的值为______．
13．某银行需要招聘一名大堂经理，应聘者王琳三项指标得分如下表，若从左至右依次赋予2∶3∶5的权重，则她的最终成绩为______分．
14．如图所示，扇形OAB的半径OB长为3，，再以点A为圆心，OA长为半径作弧，交弧AB于点C，则阴影部分的面积是______．
15．在矩形ABCD中，，，点P在BC边上，．若点E是矩形ABCD边上一点，且是以BE为底边的等腰三角形，则BE的长是______．
三、解答题（本大题共8个小题，满分75分）
16．（10分）
（1）计算：；（2）化简：．
17．（9分）2024年春节前夕，河南某地文旅部门出大招：个人可在朋友圈自己策划文案并配美图对本地景区进行宣传，凡是获奖者可获得景区免费年票．组织者随机抽取若干作品进行评估，分为优、良、中、差四个等级（优秀作品可获免费年票），并绘制了如图所示两幅不完整统计图．
（1）本次抽取的作品数量为______，______；
（2）请补全条形统计图；
（3）若本次活动共有12000名参与者，请估计参与者中能获得景区免费年票的人数．
18．（9分）如图所示，一次函数和反比例函数的图象交于点，与y轴交于点A．
第18题图
（1）求反比例函数的解析式；
（2）将直线AB向下平移使其经过原点，与的图象交于点C，连接AC，BC，求的面积．
19．（9分）电动切割机以其高效、准确和便捷的特点，成为现代工作中不可或缺的工具，图1是从电动切割机抽象出来的几何模型，ON为固定台，切割片与摆臂OM相切于点P，图2是切割机完成工作时候的模型图，此时切割片与ON相切．已知切割片的半径为30cm，转轴OA长是60cm，（此次切割片在工作时候的磨损忽略不计）．
第19题图
（1）求图2中点B到OM的距离；
（2）求砂轮工作前后，圆心A运动轨迹长度．
20．（9分）汝南著名传统土特产品“五香大头菜”、“鸡汁豆腐干”深受广大消费者喜爱．已知2件大头菜和1件豆腐干进货价为160元，1件大头菜和3件豆腐干进货价为180元．
（1）分别求出每件大头菜、豆腐干的进价；
（2）某特产店计划购进大头菜、豆腐干共60件，且大头菜的数量不高于豆腐干数量的．若该特产店每件大头菜售价为80元，每件豆腐干售价为55元，怎样进货可使该特产店获得利润最大，最大利润为多少元？
21．（9分）宝岩寺塔始建于北宋时期，已有近千年的历史，为仿木结构楼阁式七级砖塔，整体呈奶黄色，平面呈六角形，塔角雕饰龙首，塔身浮雕壁画，如今已经成为驻马店西平县的地标性建筑．某实践探究小组想测得宝岩寺塔的高度，数据勘测组通过勘测，得到了如下记录表：
22．（10分）如图所示，某设计公司在半径为4.5m的圆形水池中心安装调试喷水器，设垂直于水平面的喷水管OA高出地面1.5m，在A处喷出的水流呈抛物线状．喷头A与水流最高点B的连线与抛物线对称轴成45°的角，抛物线最高点B与喷水头A的落差为2m，水流的水平落点为D．
（1）求抛物线的函数解析式；
（2）水流落点D是否落在水池外？请说明理由；
（3）在水压不变的情况下，请问如何调整喷头位置可使水流恰好落在池内？
23．（10分）【问题情境】在数学活动课上，奋飞组的同学在延时课上用两张矩形纸片进行探究活动．小组同学准备了两张矩形纸片ABCD和EBGF，其中，，将它们按如图1所示的方式放置，点E，G分别落在AB，BC边上时，点E，G恰好为边AB，BC的中点．然后将矩形纸片EBFG绕点B按顺时针方向旋转，旋转角为α，连接AE与CG．
【观察发现】
（1）如图2所示，当时，小组成员发现AE与CG存在的数量关系为______；位置关系为______；
【探索猜想】
（2）如图3所示，当时，（1）中发现的结论是否仍然成立？请说明理由；
【拓展延伸】
（3）在矩形EBFG的旋转过程中，连接AG，CE，得为定值，请直接写出此定值．
数学参考答案
说明：
1．如果考生的解答与本参考答案提供的解法不同，可根据提供的解法的评分标准精神进行评分．
2．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．
如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定对后面给分的多少，但原则上不超过后继部分应得分数之半．
3．评分标准中，如无特殊说明，均为累计给分．
4．评分过程中，只给整数分数．
一、选择题（每小题3分，共30分）
1．C【解析】∵，，，∴．∴最大的数是2．故选C．
2．B【解析】将120亿用科学记数法表示为．故选B．
3．D【解析】该几何体的俯视图如下图所示．故选D．
4．A【解析】原式．故选A．
5．D【解析】由作图痕迹得PQ垂直平分AB，∴，，．故D不一定成立．故选D．
6．B【解析】∵，，∴．∵，∴．∴．故选B．
7．C【解析】关于x的一元二次方程整理为一般式为．∵关于x的一元二次方程有两个不相等的实数根，∴，解得．∴m的值可以是2．故选C．
8．C【解析】根据题意，画出如下所示的树状图．摆出的三位数有6个，其中能被4整除的是132，312．所以摆出的三位数能被4整除的概率为．故选C．
9．A【解析】根据一次函数图象，得，．所以二次函数的图象开口向下，经过坐标原点，且对称轴在y轴左侧．故选A．
10．C【解析】∵四边形ABCD为矩形，，，，根据折叠性质得，，，．∴为等腰三角形，．∵，，∴．∴为等腰三角形，．
∴．在中，．故选C．
二、填空题（每小题3分，共15分）
11．【解析】由题意可得，解得．
12．3【解析】由（②＋①），得．
13．83【解析】王琳的最终成绩为：（分）．
14．【解析】连接AC，OC．在扇形AOB中，，，以A为圆心，OA长为半径画弧，∴．∴是等边三角形．∴．
∴，，．
∴．∴．
15．或【解析】如图所示，点E具有不固定性，故讨论如下：①当点E在AD边上时，如图1所示，此时是等腰直角三角形，∴底边；②当点E在CD边上时，，∴．综上，BE的长为或．
三、解答题（本大题共8个小题，满分75分）
16．解：（1）原式（3分）
．（5分）
（2）原式（3分）
．（5分）
17．解：（1）30 108（4分）
（2）样本中为“中”的作品数为（个），
补全条形统计图如下图所示．（6分）
（3）（人）．
答：参与者中能获得景区免费年票的人数约为3600人．（9分）
18．解：（1）把代入，得，
解得．
∴．（2分）
把代入，得，解得．
∴反比例函数的解析式为．（4分）
（2）过点B作轴于E，交AC于点D，如图所示．
将直线AB向下平移使其经过原点，其函数解析式为．
联立解析式，得解得
∴C点坐标为．（5分）
设直线AC的函数解析式为．
将，代入，得解得
∴直线AC的函数解析式为．（7分）
在中，当时，．
∴．∴．
∴的面积为3．（9分）
19．解：（1）过点B作，，垂足分别为Q，C．
∴cm，cm．
∴由勾股定理得（cm）．（2分）
∵，∴四边形BCOQ为矩形．
∴（cm）．
∴点B到OM的距离为cm．（5分）
（2）在中，，∴（7分）
同理可得．
∴．
∴圆心A运动轨迹的长为（cm）．（9分）
20．解：（1）设每件大头菜的进价为x元，每件豆腐干的进价为y元．
根据题意，得解得
∴每件大头菜的进价为60元，每件豆腐干的进价为40元．（4分）
（2）设购进大头菜a件，则购进豆腐干件．
根据题意，得，解得．（6分）
设总利润为w元．
则．
∵，∴w随a的增大而增大．
∴当时，w取得最大值，最大值为．
∴购进大头菜15件，豆腐干45件，可使该特产店获得利润最大，最大利润为975元．（9分）
21．解：设（m）．
在中，，
∴（m）．（4分）
在中，，∴（m）．（7分）
∴，
解得．
答：宝严寺塔的高度约为28.8m．（9分）
22．解：（1）过点A作，垂足为E．
由题知，A点坐标为，．
∴为等腰直角三角形．∴．∴B点坐标为．
设抛物线的函数解析式为．
将点代入，得，解得．
∴抛物线的解析式为．（3分）
（2）水流落点D落在水池外．（4分）
理由：∵D点为抛物线的图象与x轴的交点，
∴当时，即：，
解得，（舍）．
∵，∴水流落点D落在水池外．（6分）
（3）设将喷头A沿铅垂方向调整k米．根据题意，得
新的函数解析式为，（7分）
将坐标代入，得，解得．
答：将喷头A向下平移0.375m可使水流恰好落在池内．（10分）
23．解：（1），（3分）
【解析】如图1所示，延长AE交CG于点H．
∵点E，G恰好为边AB，BC的中点，∴，．
∵四边形ABCD和EBGF是矩形，，∴．
∵，，∴．∴，．
由“8”字模型得，∴．
（2）当时，（1）中发现的结论仍然成立．（4分）
理由：如图2所示，∵四边形ABCD和EBGF是矩形，∴．
∴．即．
∵，，∴．
∴，．（6分）
设BC与AE交于点P，AE与CG交于点O，由“8”字模型得，
∴．（7分）
∴当时，AE与CG的数量关系是；位置关系是．
（3）的定值为125．（10分）
提示如下：连接AC，GE，由（2）得，∴四边形ACEG为垂美四边形．
∴．
应聘者
信息处理
人际沟通
理解判断
王琳
80
90
80
实践探究活动记录表
活动内容：宝岩寺塔的高度 活动日期：2024年3月12日
成员 组长：×× 组员：××××××××××××
工具：测角仪，皮尺等
测量示意图
说明：塔高无法直接测量，数据勘测组在A，B两处通过测角仪可测得，的度数，以及使用皮尺测得AB的长度．
测量数据
角的度数
边的长度
米
计算数据
求塔高（CD）．
（结果精确到0.1m．参考数据：，，，）
特殊说明
（点A，B，C，D在同一平面内，且点A，B，C在同一水平线上）