2024年河南省驻马店市泌阳县中考数学一模试卷（含解析）

这是一份2024年河南省驻马店市泌阳县中考数学一模试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列四组数中，互为相反数的是( )
A. (−1)2024和(−1)2023B. 23和−32
C. −(−5)和|−5|D. (−3)3和−33
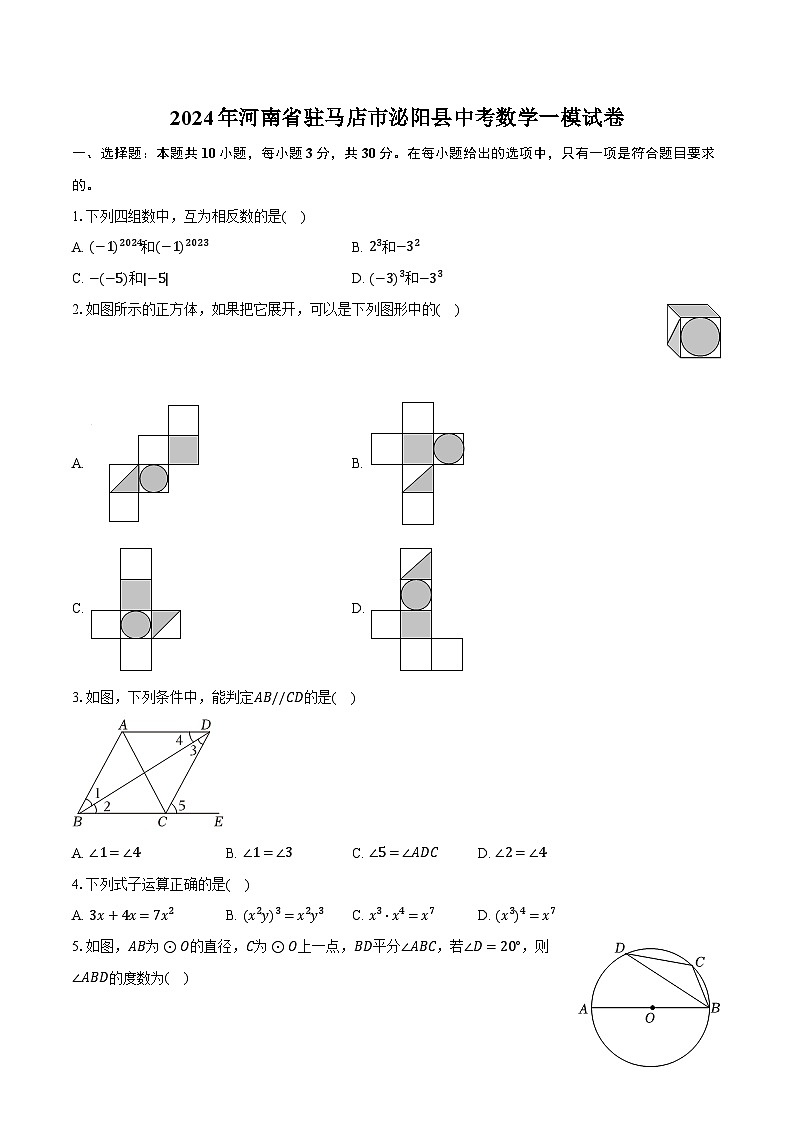
2.如图所示的正方体，如果把它展开，可以是下列图形中的( )
A. B.
C. D.
3.如图，下列条件中，能判定AB/​/CD的是( )
A. ∠1=∠4B. ∠1=∠3C. ∠5=∠ADCD. ∠2=∠4
4.下列式子运算正确的是( )
A. 3x+4x=7x2B. (x2y)3=x2y3C. x3⋅x4=x7D. (x3)4=x7
5.如图，AB为⊙O的直径，C为⊙O上一点，BD平分∠ABC，若∠D=20°，则∠ABD的度数为( )
A. 20°
B. 25°
C. 30°
D. 35°
6.2023年10月26日神舟十七号载人飞船发射取得圆满成功，我国载人航天工程发射任务实现30战30捷，航天员在中国空间站俯瞰地球的高度约为400000米，将400000用科学记数法表示应为( )
A. 4×105B. 4×106C. 40×104D. 0.4×106
7.我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，一位母亲在从右到左依次排列的绳子上打结，采取满七进一的方式，用来记录孩子自出生后的天数.例如图1表示的是孩子出生后30天时打绳结的情况(因为：4×71+2×70=30)，那么由图2可知，孩子出生后的天数是天．( )
A. 510B. 511C. 513D. 520
8.如图所示，把两张矩形纸条交叉叠放在一起，重合部分构成一个四边形ABCD.固定一张纸条，另一张纸条在转动过程中，下列结论一定成立的是( )
A. 四边形ABCD的周长不变
B. 四边形ABCD的面积不变
C. AD=AB
D. AB=CD
9.如图，在平面直角坐标系中，O是菱形ABCD的对角线BD的中点，AD/​/x轴且AD=8，∠A=60°，点C的坐标是( )
A. (4 3,4)
B. (4 3,−4)
C. (6,2 3)
D. (6,−2 3)
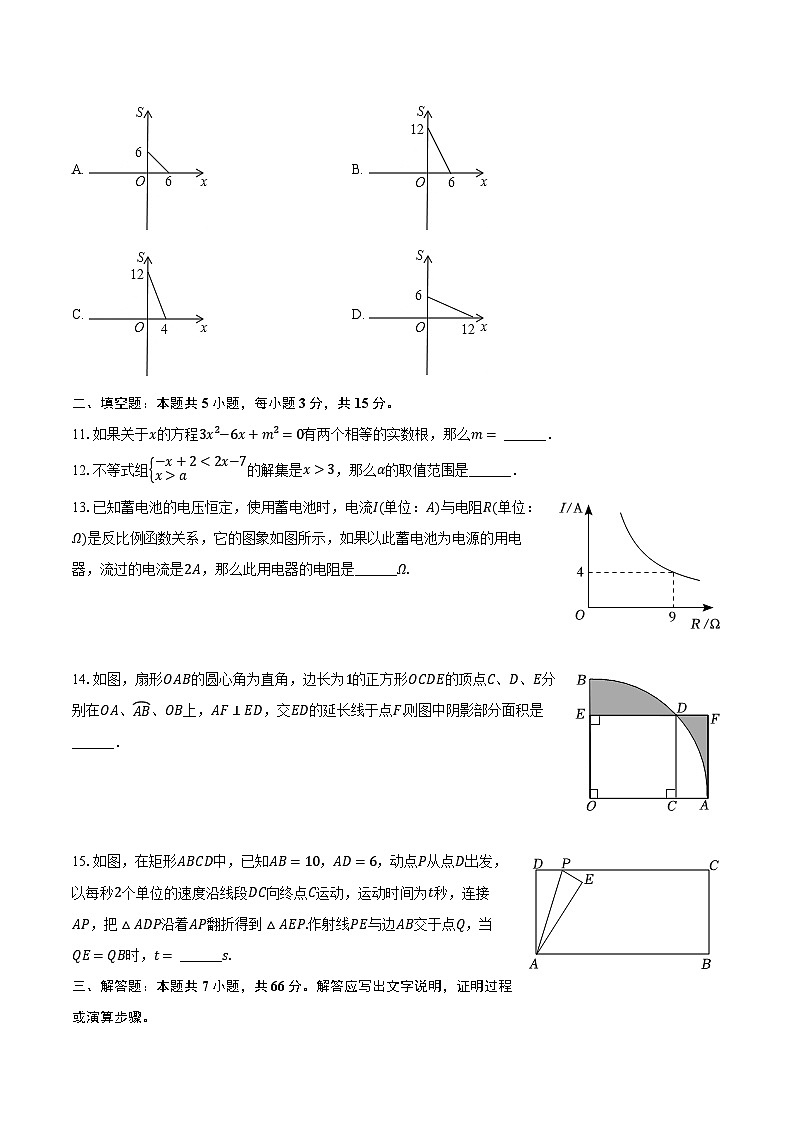
10.点P(x,y)在第一象限内，且x+y=6，点A的坐标为(4,0).设△OPA的面积为S，则下列图象中，能正确反映S与x之间的函数关系式的是( )
A. B.
C. D.
二、填空题：本题共5小题，每小题3分，共15分。
11.如果关于x的方程3x2−6x+m2=0有两个相等的实数根，那么m= ______．
12.不等式组−x+2<2x−7x>a的解集是x>3，那么α的取值范围是______．
13.已知蓄电池的电压恒定，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，流过的电流是2A，那么此用电器的电阻是______Ω.
14.如图，扇形OAB的圆心角为直角，边长为1的正方形OCDE的顶点C、D、E分别在OA、AB、OB上，AF⊥ED，交ED的延长线于点F.则图中阴影部分面积是______．
15.如图，在矩形ABCD中，已知AB=10，AD=6，动点P从点D出发，以每秒2个单位的速度沿线段DC向终点C运动，运动时间为t秒，连接AP，把△ADP沿着AP翻折得到△AEP.作射线PE与边AB交于点Q，当QE=QB时，t= ______s.
三、解答题：本题共7小题，共66分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题10分)
(1)计算：−12024+|−6|−(−3.14−π)0+(−13)−2；
(2)化简：(1−aa+2)÷a2−4a2+4a+4÷a2−4a2+4a+4．
17.(本小题9分)
全球工业互联网大会永久会址落户沈阳.为了让学生了解工业互联网相关知识，某校准备开展“工业互联网”主题日活动，聘请专家为学生做五个领域的专题报告：A.数字孪生；B.人工智能；C.应用5G；D.工业机器人；E.区块链.为了解学生的研学意向，在随机抽取的部分学生中下发如图所示的调查问卷，所有问卷全部收回且有效，根据调查数据绘制成两幅不完整的统计图．

请根据统计图提供的信息，解答下列问题：
(1)求本次调查所抽取的学生人数，并直接补全条形统计图；
(2)求扇形统计图中领域“B”对应扇形的圆心角的度数；
(3)学校有600名学生参加本次活动，地点安排在两个多功能厅，每场报告时间为90分钟.由下面的活动日程表可知，A和C两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下，请你合理安排B，D，E三场报告，补全此次活动日程表(写出一种方案即可)，并说明理由．
18.(本小题9分)
如图，一次函数y=kx+b的图象与反比例函数y=mx的图象交于点A，B(2,n)，与x轴交于点C(1,0)，点D在第三象限，且CD⊥AB，CD=AC．
(1)利用尺规作出点D(不写作法，保留作图痕迹)；
(2)若D(−2,−2)，求反比例函数与一次函数的解析式．
19.(本小题9分)
某品牌大米远近闻名，深受广大消费者喜爱，某超市每天购进一批成本价为每千克4元的该大米，以不低于成本价且不超过每千克7元的价格销售.当每千克售价为5元时，每天售出大米950kg；当每千克售价为6元时，每天售出大米900kg，通过分析销售数据发现：每天销售大米的数量y(kg)与每千克售价x(元)满足一次函数关系．
(1)请直接写出y与x的函数关系式；
(2)超市将该大米每千克售价定为多少元时，每天销售该大米的利润可达到1800元？
(3)当每千克售价定为多少元时，每天获利最大？最大利润为多少？
20.(本小题9分)
中国5A级旅游景区开封市清明上河园中水车园的水车由立式水轮、竹筒、支撑架、水槽等部件组成，如图是水车园中半径为5m的水车灌田的简化示意图，立式水轮⊙O在水流的作用下利用竹筒将水运送到点A处，水沿水槽AP流到田地，⊙O与水面交于点B，C，且点B，C，P在同一直线上，且∠PAC=∠PBA，若点P到点C的距离为32m，立式水轮⊙O的最低点到水面的距离为2m.连接AC，AB．
(1)求证：AP是⊙O的切线；
(2)请求出水槽AP的长度．
21.(本小题10分)
如图，在某中学的一场篮球赛中，李明在距离篮圈中心5.5m(水平距离)处跳起投篮，球出手时离地面2.2m，当篮球运行的水平距离为3m时达到离地面的最大高度4m.已知篮球在空中的运行路线为一条抛物线，篮圈中心距地面3.05m．
(1)建立如图所示的平面直角坐标系，求篮球运动路线所在抛物线的函数解析式；
(2)场边看球的小丽认为，李明投出的此球不能命中篮圈中心.请通过计算说明小丽判断的正确性；
(3)在球出手后，未达到最高点时，被防守队员拦截下来称为盖帽.但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规.在(1)的条件下，防守方球员张亮前来盖帽，已知张亮的最大摸球高度为3.2m，则他应该在李明前面多少米范围内跳起拦截才能盖帽成功？
22.(本小题10分)
小贺同学在数学探究课上，用几何画板进行了如下操作：首先画一个正方形ABCD，一条线段OP(OP
(1)【探究发现】如图1，BE与DG的大小和位置关系：______．
(2)【尝试证明】如图2，将正方形AEFG绕圆心A转动，在旋转过程中，上述(1)的关系还存在吗？请说明理由．
(3)【思维拓展】如图3，若AB=2OP=4，则：
①在旋转过程中，点B，A，G三点共线时，CF的值为______；
②在旋转过程中，CF的最大值是______．
答案和解析
1.【答案】A
【解析】解：A.∵(−1)2024=1，(−1)2023=−1，1和−1是互为相反数，∴(−1)2024与(−1)2023是互为相反数，故此选项符合题意；
B.∵23=8，−32=−9，∴23与−32不是互为相反数，故此选项不符合题意；
C.∵−(−5)=5，|−5|=5，∴−(−5)=|−5|，故此选项不符合题意；
D.∵(−3)3=−27，−33=−27，∴(−3)3=−33，故此选项不符合题意；
故选：A．
A、B选项根据乘方的意义进行计算，然后判断即可；
C选项根据互为相反数定义和绝对值的性质进行计算，然后判断即可；
D选项根据立方的意义进行计算，然后判断即可．
本题主要考查了实数的运算，解题关键是熟练掌握乘方和立方的意义．
2.【答案】B
【解析】解：A、D折叠后阴影部分是正方形的面与阴影部分是三角形的面相对，与原图不符，故A、D不符合题意，
而C折叠后，圆形在前面，正方形在上面，则三角形的面在右面，与原图不符，故C不符合题意，
只有B折叠后符合，
故选：B．
根据正方体的展开图的特征，“对面”“邻面”之间的关系进行判断即可．
考查正方体的展开与折叠，掌握展开图的特征以及“正面、邻面”之间的关系是正确判断的前提．
3.【答案】B
【解析】解：A.∠1=∠4，不能判定AB/​/CD，故该选项不正确，不符合题意；
B.∵∠1=∠3，∴AB/​/CD，故该选项正确，符合题意；
C.∵∠5=∠ADC，∴AD/​/BC，故该选项不正确，不符合题意；
D.∠2=∠4，∴AD/​/BC，故该选项不正确，不符合题意；
故选：B．
根据平行线的判定定理即可作出判断．
本题考查了平行线的判定定理，熟练掌握平行线的判定定理是解题的关键．
4.【答案】C
【解析】解：A.3x与4x是同类项，可以合并，3x+4x=7x，A不符合题意；
B.根据“积的乘方，需要把积中的每一个因式分别乘方，再把所得的积相乘”知(x2y)3=x6y3，B不符合题意；
C.根据“同底数幂相乘，底数不变，指数相加”知x3⋅x4=x3+4=x7，C符合题意；
D.根据“幂的乘方，底数不变，指数相乘”知(x3)4=x12，D不符合题意，
故选：C．
根据合并同类项，积的乘方，同底数幂的乘法，幂的乘方可进行判断．
本题考查了合并同类项，积的乘方，同底数幂的乘法，幂的乘方，关键是熟记法则求解．
5.【答案】D
【解析】解：如图，连接AC，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠A+∠ABC=90°，
∵∠D=∠A=20°，
∴∠ABC=70°，
∵BD平分∠ABC，
∴∠ABD=12∠ABC=35°，
故选：D．
根据圆周角定理得出∠ACB=90°，∠A=20°，根据直角三角形的性质求出∠ABC=70°，根据角平分线的定义求解即可．
此题考查了圆周角定理，熟记圆周角定理是解题的关键．
6.【答案】A
【解析】解：400000=4×105，
故选：A．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|<10，n为整数，且n比原来的整数位数少1，据此判断即可．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
7.【答案】A
【解析】解：1×73+3×72+2×7+6=510(天)，
答：孩子自出生后的天数是510天．
故选：A．
类比于现在我们的十进制“满十进一”，可以表示满七进一的数为：千位上的数×73+百位上的数×72+十位上的数×7+个位上的数，再列式计算即可．
本题考查了计数方法，有理数的混合运算，解答本题的关键是熟练掌握有理数混合运算法则．
8.【答案】D
【解析】解：设两张纸条的宽为h，
∵纸条的对边平行，
∴AD/​/BC，AB//DC，
∴四边形ABCD是平行四边形．
又∵S▱ABCD=BC⋅h=CD⋅h，
∴BC=CD，
∴四边形ABCD是平行四边形，
∴AD=AB．
故选：D．
设两张等宽的纸条的宽为h，由条件可知AB/​/CD，AD//BC，可证明四边形ABCD为平行四边形，根据平行四边形的面积公式得到BC=CD，根据菱形的判定和性质定理即可得到结论．
本题考查了菱形的判定和性质，面积法等知识，掌握矩形的性质是解题的关键．
9.【答案】D
【解析】解：如图所示，设AD与y轴交于点E，
∵四边形ABCD是菱形，
∴AD=AB，
∵AD=8，∠A=60°，
∴△ABD是等边三角形，则BD=AD=8，
∵O是菱形ABCD的对角线BD的中点，
∴OD=12BD=4
∵AD/​/x轴，则∠DEO=90°，
∴∠EOD=30°
∴DE=12OD=2，OE= OD2−ED2=2 3，
∴A(−6,2 3)
∵A，C关于O对称，
∴C(6,−2 3)，
故选：D．
根据题意得出△ABD是等边三角形，则BD=AD=8，根据含30度角的直角三角形的性质，勾股定理求得DE，OE，进而得出A点的坐标，根据中心对称的性质即可求解．
本题考查坐标与图形，菱形的性质，勾股定理，等边三角形的性质与判定，含30度角的直角三角形的性质，求得点A的坐标是解题的关键．
10.【答案】B
【解析】解：∵点P(x,y)在第一象限内，且x+y=6，点A的坐标为(4,0)，
∴S=4y2=2y=2(6−x)=−2x+12，x>0且x<6，
∴0故选：B．
根据点P(x,y)在第一象限内，且x+y=6，点A的坐标为(4,0)，从而可以得到S关于x的函数关系式，从而可以解答本题．
本题考查函数图象、三角形的面积，解答本题的关键是明确题意，列出相应的函数关系，利用数形结合的思想解答．
11.【答案】± 3
【解析】解：∵关于x的方程3x2−6x+m2=0有两个相等的实数根，
∴Δ=b2−4ac=0，
即(−6)2−4×3×m2=0，
解得m=± 3，
故答案为：± 3．
因为一元二次方程有两个相等的实数根，所以Δ=b2−4ac=0，根据判别式列出方程求解即可．
本题考查了一元二次方程根的情况与判别式△的关系：
(1)Δ>0⇔方程有两个不相等的实数根；
(2)Δ=0⇔方程有两个相等的实数根；
(3)Δ<0⇔方程没有实数根．
12.【答案】a≤3
【解析】解：−x+2<2x−7①x>a②，
解不等式①得：x>3，
解不等式②得：x>a，
∵不等式组的解集是x>3，
∴a≤3，
故答案为：a≤3．
按照解一元一次不等式组的步骤，进行计算即可解答．
本题考查了解一元一次不等式组，熟练掌握解一元一次不等式组的步骤是解题的关键．
13.【答案】18
【解析】解：设反比例函数关系式为：I=kR，
把(4,9)代入得：k=4×9=36，
∴反比例函数关系式为：I=36R，
当I=2时，则2=36R，
∴R=18，
故答案为：18．
根据图象中的点的坐标先求反比例函数关系式，再由电流为2A求得电阻即可．
本题是反比例函数的应用，会利用待定系数法求反比例函数的关系式，并正确认识图象，运用数形结合的思想，与不等式或等式相结合，解决实际问题．
14.【答案】 2−1
【解析】解：连接OD，
∵正方形的边长为1，即OC=CD=1，
∴OD= OC2+CD2= 2，
∴AC=OA−OC= 2−1，
∵DE=DC，BE=AC，弧BD=弧AD，
∴图形ACD是面积等于图形BED的面积，
∴S阴=长方形ACDF的面积=AC⋅CD= 2−1．
故答案为： 2−1．
通过观察图形可知DE=DC，BE=AC，弧BD=弧AD，阴影部分的面积正好等于长方形ACDF的面积，根据正方形的性质求出扇形的半径，从而求出AC的长，即可求出长方形ACDF的面积．
本题要把不规则的图形通过几何变换转化为规则图形的面积求解．如通过观察可知阴影部分的面积正好等于长方形ACDF的面积，直接根据相关条件求长方形ACDF的面积即可．
15.【答案】95或5
【解析】解：分两种情况：
当点E在矩形ABCD内部时，过P作PH⊥AB于H，过Q作QG⊥CD于G，如图，
∴PH=QG=AD=6，
∵∠APQ=∠APD=∠PAQ，
∴AQ=PQ，
∵PQ2=PG2+QG2=PG2+62=36+PG2，
∴AQ2=36+PG2，
∵AQ=DG=DP+PG，
∴(DP+PG)2=36+PG2，
∵PD=2t，
∴(2t+PG)2=36+PG2，
解得：PG=9−t2t，
∵AQ=PD+PG=2t+9−t2t=t2+9t，
∵QE=PQ−PE=PQ−DP=PQ−2t，
∵QE=QB，PQ=AQ，
∴QB=AQ−2t，
∵AQ+BQ=AB=10，
∴AQ+AQ−2t=10，
∴AQ=5+t，
∴5+t=t2+9t，
解得t=95；
当点E在矩形ABCD的外部时，如图：
∵∠APQ=∠APD=∠PAQ，
∴AQ=PQ，
∵QE=PE−PQ=DP−PQ=2t−PQ，QE=QB，
∴BQ=2t−AQ，即AB−AQ=2t−AQ，
∴AB=2t，
∴t=AB2=5(此时P与C重合)，
综上，存在这样的t值，使得QE=QB，t的值为95或5．
故答案为：95或5．
分两种情况：点E在矩形的内部和外部，根据等量关系列方程可解答．
本题考查翻折变换，矩形的性质、几何动点问题，轴对称的性质等知识，解题的关键是学会正确画出图形，学会分类讨论，充分利用轴对称的性质解决问题．
16.【答案】解：(1)原式=−1+6−1+9
=13；
(2)原式=a+2−aa+2⋅(a+2)2(a+2)(a−2)
=2a+2⋅(a+2)2(a+2)(a−2)
=2a−2．
【解析】(1)先算乘方，去绝对值，再算加减；
(2)先通分算括号内的，把除化为乘，再约分即可．
本题考查实数混合运算和分式混合运算，解题的关键是掌握实数，分式相关运算的法则．
17.【答案】解：(1)本次调查所抽取的学生人数为4÷10%=40(人)，
意向领域“D”的人数为40−(4+6+10+8)=12(人)，
补全条形统计图如下：

(2)360°×640×100%=54°，
答：扇形统计图中领域“B”对应扇形的圆心角的度数为54°；
(3)意向领域“B”的人数为600×640=90(人)，
意向领域“D”的人数为600×1240=180(人)，
意向领域“E”的人数为600×840=120(人)，
补全此次活动日程表如下：

【解析】(1)根据意向领域“A”的人数及其百分比求得总人数，用总人数减去其它领域的人数求出意向领域“D”的人数即可补全条形统计图；
(2)用360°乘以意向领域“B”的百分比即可；
(3)分别求出意向领域“B”“D”“E”的人数，补全此次活动日程表即可．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
18.【答案】解：(1)如图，点D为所作；
；
(2)作AE⊥x轴于E，DF⊥x轴于F，

∵D(−2,−2)，C(1,0)，
∴DF=2，CF=3，
∵∠ACE+∠FCD=90°=∠FCD+∠FDC，
∴∠ACE=∠FDC，
∵∠AEC=∠CFD=90°，AC=CD，
∴△ACE≌△CDF(AAS)，
∴AE=CF=3，CE=DF=2，
∴OE=1，
∴A(−1,3)，
∵反比例函数y=mx的图象过点A，
∴m=−1×3=−3，
∴反比例函数为y=−3x，
∵一次函数y=kx+b的图象过点A(−1,3)，C(1,0)，
∴−k+b=3k+b=0，
解得k=−32b=32，
∴一次函数的解析式为y=−32x+32．
【解析】(1)以C为圆心，任意长为半径画弧交AB于两点P、Q，分别以P、Q为圆心以大于12PQ长为半径画弧，交于点K，过点K、C作直线CK，在CK上截取CD=AC，使D在第三象限；
(2)作AE⊥x轴于E，DF⊥x轴于F，通过证得△ACE≌△CDF(AAS)，求得A(−1,3)，然后利用待定系数法即可求得反比例函数和一次函数的解析式．
本题考查了反比例函数和一次函数的交点问题，待定系数法求一次函数和反比例函数的解析式、三角形全等的判断和性质，求得点A的坐标是解题的关键．
19.【答案】解：(1)根据题意设y=kx+b，
当每千克售价为5元时，每天售出大米950kg；
当每千克售价为6元时，每天售出大米900kg，
则5k+b=9506k+b=900，
解得：k=−50b=1200，
则y与x的函数关系式；y=−50x+1200(4≤x≤7)，
(2)∵定价为x元，每千克利润(x−4)元，
由(1)知销售量为y=−50x+1200(4≤x≤7)，
则(x−4)(−50x+1200)=1800，
解得：x1=22(舍)，x2=6，
∴超市将该大米每千克售价定为6元时，每天销售该大米的利润可达到1800元；
(3)设利润为W元，
根据题意可得：W=(x−4)(−50x+1200)，
即W=−50x2+1400x−4800=−50(x−14)2+5000，
∵a=−50<0，对称轴为x=14，
∴当x<14时，W随x的增大而增大，
又∵4≤x≤7，
∴x=7时，W最大值=−50(7−14)2+5000=2550元
∴当每千克售价定为7元时，每天获利最大，最大利润为2550元．
【解析】(1)根据题意设y=kx+b，当每千克售价为5元时，每天售出大米950kg；当每千克售价为6元时，每天售出大米900kg，则5k+b=9506k+b=900，求得k、b即可；
(2)定价为x元，每千克利润(x−4)元，销售量为y kg，则(x−4)y=1800即(x−4)(−50x+1200)=1800，解方程即可；
(3)设利润为W，根据题意可得W=(x−4)(−50x+1200)=−50x2+1400x−4800化为顶点式即可求出合适的值．
本题考查二次函数的应用以及一元二次方程的解法，属于综合题，关键是理解题意，搞清楚数量关系．
20.【答案】(1)证明：连接AO，并延长AO交⊙O于D，连接CD，则∠ACD=90°，

∴∠CAD+∠CDA=90°，
∵∠ABC=∠ADC，∠PAC=∠PBA，
∴∠PAC=∠ADC，
∴∠CAD+∠PAC=90°，
∵OA是半径，
∴AP与⊙O相切，
(2)解：如图，OF⊥BP于点E，且EF=2米，

∵OF=5米，
∴OE=OF−EF=5−2=3(米)，
连接OC，
∴EC= OC2−OE2= 52−32=4(米)，
∴BC=2OC=8米，
∵PC=32米，
∴PB=CP+CB=32+8=40(米)，
∵∠PAC=∠PBA，∠CPA=∠APB，
∴△CAP∽△ABP，
∴APPB=CPAP，
∴AP2=PB⋅CP=40×32=1280，
∴AP=16 5(米)．
【解析】(1)连接AO，并延长AO交⊙O于D，连接CD，则∠ACD=90°，由切线的性质及圆周角定理可得出结论；
(2)由勾股定理求出CE=4米，证明△CAP∽△ABP，得出APPB=CPAP，可求出答案．
本题考查了切线的性质，圆周角定理，相似三角形的判定与性质，勾股定理，熟练掌握切线的性质是解题的关键．
21.【答案】解：(1)∵抛物线顶点坐标为(3,4)，
∴设抛物线的解析式为y=a(x−3)2+4．
把(0,2.2)代入，得a=−15．
∴y=−15(x−3)2+4；
(2)把x=5.5代入抛物线解析式y=−15×(x−3)2+4，
得y=114．
∵114≠3.05，
∴此球不能投中，小丽的判断是正确的．
(3)当y=3.2时，3.2=−15(x−3)2+4，
解之，得x=1或x=5．
∵5>3，
∴x=1．
答：张亮应在李明前面1米范围内处跳起拦截才能盖帽成功．
【解析】(1)由题意可知，抛物线的顶点坐标为(3,4)，求出手时的坐标为(0,2.2)，设抛物线的解析式为y=a(x−3)2+4，由待定系数法求解即可；
(2)求得当x=5.5时的函数值，与3.05比较即可说明小丽判断的正确性；
(3)将y=3.2代入函数的解析式求得x的值，进而得出答案．
本题考查了二次函数在实际问题中的应用，数形结合并熟练掌握二次函数的性质是解题的关键．
22.【答案】BE=DG，BE⊥DG 2 10 6 2
【解析】解：(1)∵四边形ABCD和四边形AEFG都是正方形，
∴AB=AD，AE=AG，∠BAD=90°，
∴AB−AE=AD−AG，BE⊥DG，
∴BE=DG，
故答案为：BE=DG，BE⊥DG；
(2)(1)中的关系存在．
如图2，延长BE交DG于点M，交AD于点N．
∵∠BAD=∠EAG=90°，
∴∠BAD−∠EAD=∠EAG−∠EAD，
∴∠BAE=∠DAG．
在△BAE和△DAG中，
AB=AD,∠BAE=∠DAG,AE=AG,
∴△BAE≌△DAG(SAS)，
∴BE=DG，∠ABE=∠ADG．
在△ABN和△MDN中，
∵∠ABN=∠MDN，∠ANB=∠DNM，
∴∠DMN=∠BAN=90°，
∴BE⊥DG．
即BE=DG且BE⊥DG；
(3)①延长GF，DC交于点Q，
∵∠QGF=∠GBC=∠BCQ=90°，
∴四边形BCQD是矩形，
∴∠CQG=90°，QG=BC=4，
∵∠DAG=∠AGQ=∠GQD=90°，
∴四边形AGQD是矩形，
∴DQ=AG=2，
∵QF=QG−FG=4−2=2，QC=QD+CD=2+4=6，
∴CF= CQ2+FQ2= 62+22=2 10．
故答案为：2 10；
②在正方形ABCD和正方形AEFG中，AB=4，AE=2，
∴AC= 42+42=4 2，AF= 22+22=2 2，
∵F的运动轨迹是以A为圆心，2 2为半径的圆，
∴当C，A，F三点共线时，CF=CA+AF，CF有最大值，
此时CF=AC+AF=4 2+2 2=6 2．
故答案为：6 2．
(1)由正方形的性质得出AB=AD，AE=AG，∠BAD=90°，则可得出结论；
(2)延长BE交DG于点M，交AD于点N，证明△BAE≌△DAG(SAS)，由全等三角形的性质得出BE=DG，∠ABE=∠ADG，则可得出结论；
(3)①延长GF，DC交于点Q，证明四边形BCQD是矩形，得出∠CQG=90°，QG=BC=4，证出四边形AGQD是矩形，由矩形的性质得出DQ=AG=2，由勾股定理可求出答案；
②求出AC和AF的长，证出F的运动轨迹是以A为圆心，2 2为半径的圆，当C，A，F三点共线时，CF=CA+AF，CF有最大值，则可得出答案．
本题是圆的综合题，考查了矩形的判定与性质，正方形的性质，勾股定理，全等三角形判定和性质，相似三角形的判定和性质，等腰直角三角形的性质，旋转的性质等，熟练掌握正方形的性质是解题关键．“工业互联网”主题日学生研学意向调查问卷
请在下列选项中选择您的研学意向，并在其后“□”内打“√”(每名同学必选且只能选择其中一项)，非常感谢您的合作．
A.数字孪生□B.人工智能□C.应用5G□D.工业机器人□E.区块链□
“工业互联网”主题日活动日程表
地点(座位数)
时间
1号多功能厅(200座)
2号多功能厅(100座)
8：00−9：30
A
10：00−11：30
C
13：00−14：30
设备检修暂停使用
“工业互联网”主题日活动日程表
地点(座位数)
时间
1号多功能厅(200座)
2号多功能厅(100座)
8：00−9：30
D
A
10：00−11：30
C
B
13：00−14：30
E
设备检修暂停使用