初中数学冀教版八年级下册第二十一章 一次函数21.1 一次函数习题ppt课件

这是一份初中数学冀教版八年级下册第二十一章 一次函数21.1 一次函数习题ppt课件，共29页。PPT课件主要包含了解题秘方等内容，欢迎下载使用。

如图，在菱形ABCD中，∠BAD＝120°，AC＝6 cm.求此菱形的周长和面积．
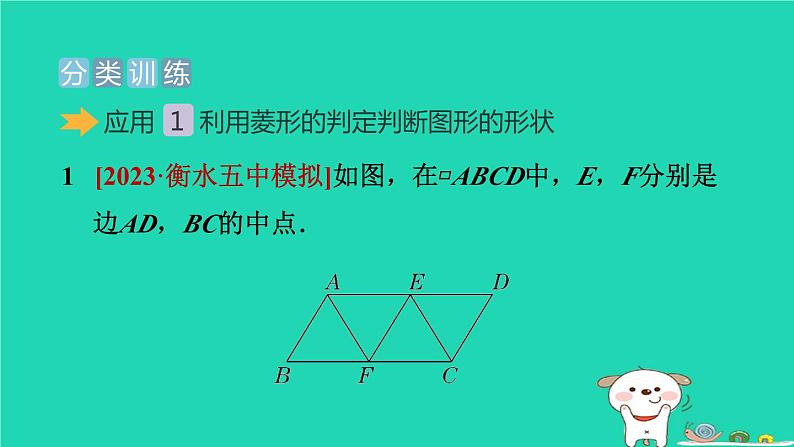
1 [2023·衡水五中模拟]如图，在▱ABCD中，E，F分别是边AD，BC的中点．
(1)求证：△ABF≌△CDE；
(2)若∠AFC＝2∠D，求证：四边形AFCE是菱形．
又∵AE∥CF，∴四边形AFCE是平行四边形．同理可证四边形CDEF是平行四边形，∴∠CFE＝∠D.∵∠AFC＝2∠D，∴∠AFE＝∠CFE＝∠D.又∵∠AEF＝∠CFE，∴∠AFE＝∠AEF.∴AF＝AE，即四边形AFCE是菱形．
2 [2023·兰州]如图，矩形ABCD的对角线AC与BD相交于点O，CD∥OE，直线CE是线段OD的垂直平分线，CE分别交OD，AD于点F，G，连接DE.
(1)判断四边形OCDE的形状，并说明理由；
【解】四边形OCDE是菱形．理由如下：∵CD∥OE，∴∠FDC＝∠FOE.∵CE是线段OD的垂直平分线，∴FD＝FO，ED＝OE，CD＝CO.
(2)当CD＝4时，求EG的长．
3 [2023·石家庄外国语学校模拟]如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF.
(1)求证：△ADE≌△CBF.
(2)连接AF，CE，当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．
【解】当BD平分∠ABC时，四边形AFCE是菱形，理由如下：∵BD平分∠ABC，∴∠ABD＝∠CBD.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，AD∥BC.∴∠ADB＝∠CBD.∴∠ABD＝∠ADB，即AB＝AD.
∴平行四边形ABCD是菱形．∴AC⊥BD.∴AC⊥EF.∵DE＝BF，∴DE＋OD＝BF＋OB，即OE＝OF.又∵OA＝OC，∴四边形AFCE是平行四边形．∵AC⊥EF，∴平行四边形AFCE是菱形．
4 [2022·青海]如图，四边形ABCD为菱形，E为对角线AC上的一个动点(不与点A，C重合)，连接DE并延长交射线AB于点F，连接BE.求证：
(1)△DCE≌△BCE；
【证明】∵四边形ABCD是菱形，∴CD＝CB，∠DCE＝∠BCE.又∵CE＝CE，∴△DCE≌△BCE(SAS)．
(2)∠AFD＝∠EBC.
【证明】∵四边形ABCD是菱形，∴DC∥AF.∴∠CDF＝∠AFD.由(1)知△DCE≌△BCE，∴∠CDF＝∠EBC.∴∠AFD＝∠EBC.
5 如图，已知▱ABCD，O为BD的中点，点E在边AD上，连接EO并延长交BC于点F，连接BE，DF.(1)求证：四边形BEDF是平行四边形；
【证明】∵四边形ABCD是平行四边形，∴AD∥BC.∴∠ODE＝∠OBF，∠OED＝∠OFB.∵O为BD的中点，∴OD＝OB.∴△ODE≌△OBF(AAS)．∴DE＝BF.又∵DE∥BF，∴四边形BEDF是平行四边形．
【解】如图，过点B作BM⊥AD交DA的延长线于点M，则∠M＝90°.
6 [2022·滨州]如图，菱形ABCD的边长为10，∠ABC＝60°，对角线AC，BD相交于点O，点E在对角线BD上，连接AE，作∠AEF＝120°且边EF与直线DC相交于点F.
(1)求菱形ABCD的面积；
(2)求证：AE＝EF.
【证明】连接EC.∵四边形ABCD是菱形，点E在对角线BD上，∠ABC＝60°，∴EO垂直平分线段AC，∠BCD＝120°.∴EA＝EC，∠DCA＝60°.∴∠EAC＝∠ECA，∠ACF＝120°.