




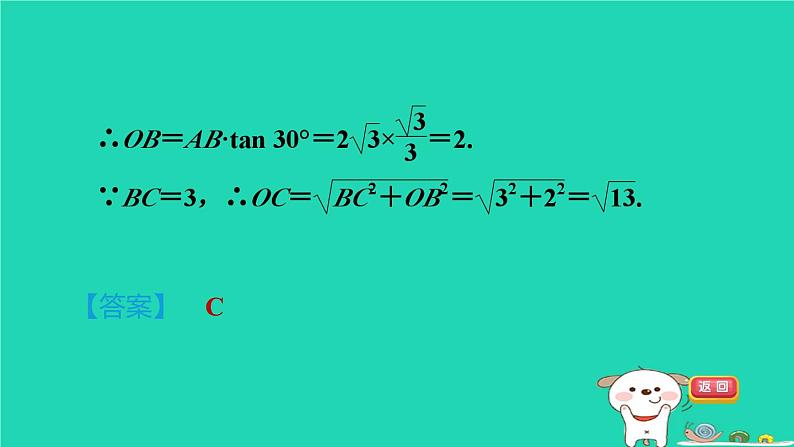
还剩30页未读,
继续阅读
2024九年级数学下册第29章直线与圆的位置关系集训课堂测素质直线与圆的位置关系习题课件新版冀教版
展开
这是一份2024九年级数学下册第29章直线与圆的位置关系集训课堂测素质直线与圆的位置关系习题课件新版冀教版,共38页。
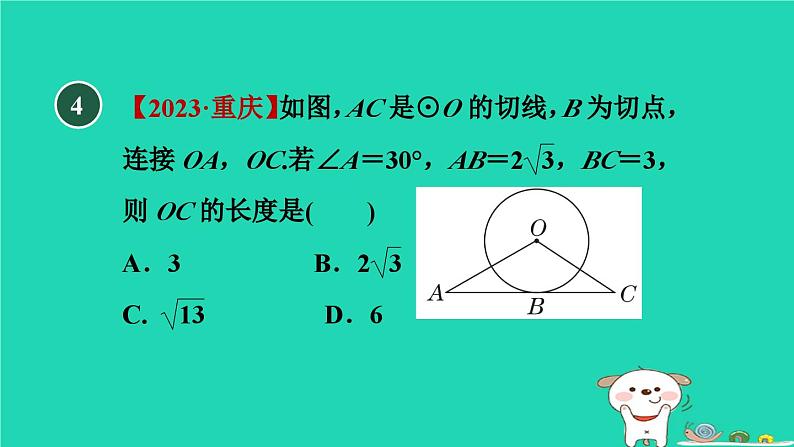
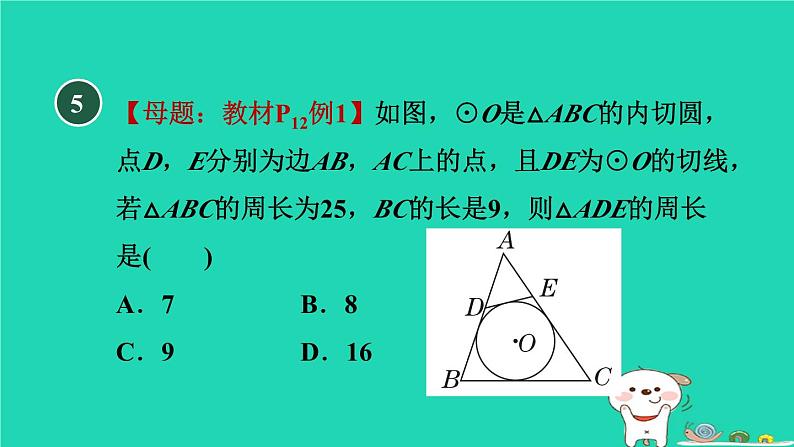
测素质 直线与圆的位置关系集训课堂 冀教版 九年级下第二十九章 直线与圆的位置关系【2023·青岛九年级测试卷】⊙O的半径为3,若点P在⊙O内,则OP的长可能为( )A.2 B.3 C.4 D.以上都有可能1一、选择题(每题4分,共32分)A2B3【2022·自贡】P为⊙O外一点,PT与⊙O相切于点T,OP=10,∠OPT=30°,则PT的长为( )A4【点拨】【答案】C5【母题:教材P12例1】如图,⊙O是△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )A.7 B.8 C.9 D.16【点拨】如图,将三角形三边及DE与圆的切点,分别标为G,I,H,F,∵⊙O是△ABC的内切圆,且DE为⊙O的切线,∴DF=DG,EF=EH,BG=BI,CH=CI.【答案】A∴△ADE的周长=AD+AE+FD+FE=AD+AE+ DG+EH=AG+AH=AB+AC-BG-CH=AB+AC- BI-CI=AB+AC-BC.∵△ABC的周长为25,BC的长是9,∴△ADE的周长=△ABC的周长-2BC=25-2×9=7.6如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线B7【2022·娄底】如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与三角形ABC的面积之比是( )【点拨】根据题意和图形,可知圆中的黑色部分的面积是圆的面积的一半,进而可计算出圆中的黑色部分的面积与三角形ABC的面积之比.【答案】A8【点拨】如图,连接OP,OQ,作OP′⊥AB于P′,∵PQ是⊙O的切线,∴OQ⊥PQ.【答案】A35°9【2023·沧州二模】如图,已知点A,Q在圆O上,连接AO,OQ,过点A作圆O的切线AP,若∠AOQ=55°,则直线AP与直线OQ相交所得的锐角度数为________.二、填空题(每题4分,共20分)210【新趋势·学科内综合】已知⊙O的半径是4,圆心O到直线l的距离是d,d是一元二次方程x2-2x-3=0的一个根,则直线l和⊙O公共点的个数是________.11【2023·北京】如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交OC的延长线于点E.若∠AOC=45°,BC=2,则线段AE的长为________.【点拨】1224【点拨】13【2022·宁波】 【新考法·分类讨论法】如图,在△ABC中,AC=2,BC=4,点O在BC上.以OB为半径的圆与AC相切于点A,D是BC边上的动点.当△ACD为直角三角形时,AD的长为________.【点拨】如图,连接OA,过点A作AD′⊥BC于点D′.∵圆与AC相切于点A,∴OA⊥AC.由题意可知,D点位置分为两种情况:(1)当∠CAD=90°时,D点与O点重合,设圆的半径为r,则OA=r,OC=4-r.14(10分) 如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于点D.求证:DI=DB.三、解答题(共48分)证明:如图,连接BI.∵I是△ABC的内心,∴AI,BI分别平分∠BAC和∠ABC.∴∠BAD=∠CAD,∠ABI=∠CBI.又∵∠DBC=∠DAC,∴∠DBC=∠BAD.∴∠ABI+∠BAD=∠CBI+∠DBC,即∠BID=∠DBI. ∴DI=DB.15(10分)【母题:教材P9练习T3】如图,正方形ABCD的边长为4,点P在边BC上,⊙O经过A,B,P三点.若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由.16(14分)【2023·福建】如图,已知△ABC内接于⊙O,CO的延长线交AB于点D,交⊙O于点E,交⊙O的切线AF于点F,且AF∥BC.证明:∵AF是⊙O的切线,∴AF⊥OA,即∠OAF=90°.∵CE是⊙O的直径,∴∠CBE=90°. ∴∠OAF=∠CBE.∵AF∥BC,∴∠BAF=∠ABC,∴∠OAF-∠BAF=∠CBE-∠ABC,即∠OAB=∠ABE,∴AO∥BE.(1)求证:AO∥BE;证明:∵∠ABE与∠ACE都是EA所对的圆周角,∴∠ABE=∠ACE.∵OA=OC,∴∠ACE=∠OAC.∴∠ABE=∠OAC.由(1)知,∠OAB=∠ABE,∴∠OAB=∠OAC,∴AO平分∠BAC.(2)求证:AO平分∠BAC.︵17(14分) 【2022·赤峰】 【新考法·等角代换法】如图,已知AB为⊙O的直径,点C为⊙O外一点,AC=BC,连接OC,DF是AC的垂直平分线,交OC于点F,垂足为点E.连接AD,CD,且∠DCA=∠OCA.证明:∵AC=BC,点O为AB的中点,∴CO⊥AB.∵DF是AC的垂直平分线,∴DC=DA.∴∠DCA=∠DAC.∵∠DCA=∠OCA,∴∠DAC=∠OCA.∴DA∥OC.∴DA⊥OA.又∵OA是⊙O的半径,∴AD是⊙O的切线.(1)求证:AD是⊙O的切线;(2)若CD=6,OF=4,求cos∠DAC的值.
测素质 直线与圆的位置关系集训课堂 冀教版 九年级下第二十九章 直线与圆的位置关系【2023·青岛九年级测试卷】⊙O的半径为3,若点P在⊙O内,则OP的长可能为( )A.2 B.3 C.4 D.以上都有可能1一、选择题(每题4分,共32分)A2B3【2022·自贡】P为⊙O外一点,PT与⊙O相切于点T,OP=10,∠OPT=30°,则PT的长为( )A4【点拨】【答案】C5【母题:教材P12例1】如图,⊙O是△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )A.7 B.8 C.9 D.16【点拨】如图,将三角形三边及DE与圆的切点,分别标为G,I,H,F,∵⊙O是△ABC的内切圆,且DE为⊙O的切线,∴DF=DG,EF=EH,BG=BI,CH=CI.【答案】A∴△ADE的周长=AD+AE+FD+FE=AD+AE+ DG+EH=AG+AH=AB+AC-BG-CH=AB+AC- BI-CI=AB+AC-BC.∵△ABC的周长为25,BC的长是9,∴△ADE的周长=△ABC的周长-2BC=25-2×9=7.6如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线B7【2022·娄底】如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与三角形ABC的面积之比是( )【点拨】根据题意和图形,可知圆中的黑色部分的面积是圆的面积的一半,进而可计算出圆中的黑色部分的面积与三角形ABC的面积之比.【答案】A8【点拨】如图,连接OP,OQ,作OP′⊥AB于P′,∵PQ是⊙O的切线,∴OQ⊥PQ.【答案】A35°9【2023·沧州二模】如图,已知点A,Q在圆O上,连接AO,OQ,过点A作圆O的切线AP,若∠AOQ=55°,则直线AP与直线OQ相交所得的锐角度数为________.二、填空题(每题4分,共20分)210【新趋势·学科内综合】已知⊙O的半径是4,圆心O到直线l的距离是d,d是一元二次方程x2-2x-3=0的一个根,则直线l和⊙O公共点的个数是________.11【2023·北京】如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC于点D,AE是⊙O的切线,AE交OC的延长线于点E.若∠AOC=45°,BC=2,则线段AE的长为________.【点拨】1224【点拨】13【2022·宁波】 【新考法·分类讨论法】如图,在△ABC中,AC=2,BC=4,点O在BC上.以OB为半径的圆与AC相切于点A,D是BC边上的动点.当△ACD为直角三角形时,AD的长为________.【点拨】如图,连接OA,过点A作AD′⊥BC于点D′.∵圆与AC相切于点A,∴OA⊥AC.由题意可知,D点位置分为两种情况:(1)当∠CAD=90°时,D点与O点重合,设圆的半径为r,则OA=r,OC=4-r.14(10分) 如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于点D.求证:DI=DB.三、解答题(共48分)证明:如图,连接BI.∵I是△ABC的内心,∴AI,BI分别平分∠BAC和∠ABC.∴∠BAD=∠CAD,∠ABI=∠CBI.又∵∠DBC=∠DAC,∴∠DBC=∠BAD.∴∠ABI+∠BAD=∠CBI+∠DBC,即∠BID=∠DBI. ∴DI=DB.15(10分)【母题:教材P9练习T3】如图,正方形ABCD的边长为4,点P在边BC上,⊙O经过A,B,P三点.若BP=3,判断边CD所在直线与⊙O的位置关系,并说明理由.16(14分)【2023·福建】如图,已知△ABC内接于⊙O,CO的延长线交AB于点D,交⊙O于点E,交⊙O的切线AF于点F,且AF∥BC.证明:∵AF是⊙O的切线,∴AF⊥OA,即∠OAF=90°.∵CE是⊙O的直径,∴∠CBE=90°. ∴∠OAF=∠CBE.∵AF∥BC,∴∠BAF=∠ABC,∴∠OAF-∠BAF=∠CBE-∠ABC,即∠OAB=∠ABE,∴AO∥BE.(1)求证:AO∥BE;证明:∵∠ABE与∠ACE都是EA所对的圆周角,∴∠ABE=∠ACE.∵OA=OC,∴∠ACE=∠OAC.∴∠ABE=∠OAC.由(1)知,∠OAB=∠ABE,∴∠OAB=∠OAC,∴AO平分∠BAC.(2)求证:AO平分∠BAC.︵17(14分) 【2022·赤峰】 【新考法·等角代换法】如图,已知AB为⊙O的直径,点C为⊙O外一点,AC=BC,连接OC,DF是AC的垂直平分线,交OC于点F,垂足为点E.连接AD,CD,且∠DCA=∠OCA.证明:∵AC=BC,点O为AB的中点,∴CO⊥AB.∵DF是AC的垂直平分线,∴DC=DA.∴∠DCA=∠DAC.∵∠DCA=∠OCA,∴∠DAC=∠OCA.∴DA∥OC.∴DA⊥OA.又∵OA是⊙O的半径,∴AD是⊙O的切线.(1)求证:AD是⊙O的切线;(2)若CD=6,OF=4,求cos∠DAC的值.
相关资料
更多










