2024春九年级数学下册第24章圆测素质与圆有关的计算作业课件新版沪科版

这是一份2024春九年级数学下册第24章圆测素质与圆有关的计算作业课件新版沪科版，共44页。
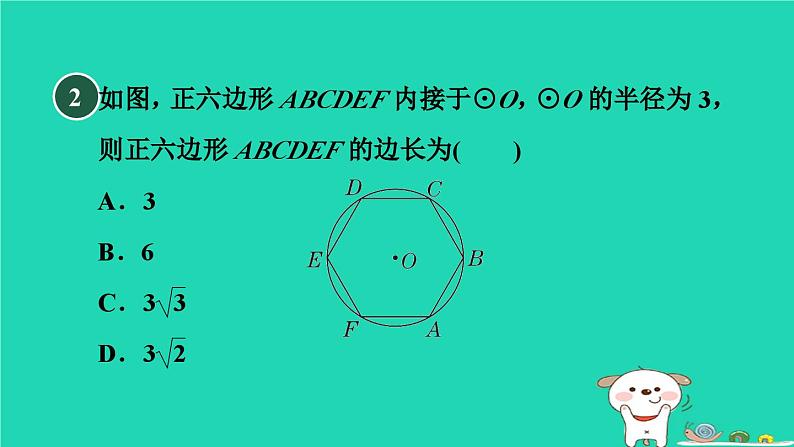
与圆有关的计算测素质第24章 圆BD答 案 呈 现BABDBA376 π3.111B一、选择题(每题4分，共32分)已知圆的半径为3，扇形的圆心角为120°，则扇形的弧长为(　　)A．π B．2π C．3π D．4π2【点拨】连接OA，OF，证明△AOF是等边三角形即可得AF的长，即正六边形的边长．【答案】A3[2023·合肥50中二模]如图，用一个圆心角为θ的扇形纸片围成一个底面半径为2，侧面积为8π的圆锥体，则该扇形的圆心角θ的大小为(　　)A．90° B．120° C．150° D．180°【点拨】【答案】D4【点拨】连接AC，易得∠BAC＝45°，∴∠BPC＝45°.【答案】B5一条弧所对的圆心角为135°，弧长等于半径为3 cm的圆的周长的5倍，则这条弧的半径为(　　)A．45 cm B．40 cm C．35 cm D．30 cmB6【点拨】如图，作AB的垂直平分线MN，作BC的垂直平分线PQ，MN与PQ相交于点O，连接OA，OC，则点O是△ABC外接圆的圆心．【答案】D7【点拨】【答案】B8【点拨】【答案】A9二、填空题(每题4分，共20分)[2023·合肥三模]用半径为9，圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计)，则这个圆锥的底面半径等于________．310一个圆的内接正三角形的边长为4，则该圆的内接正方形的边长为________．2023年旅游业迎来强势复苏．某古城为了吸引游客，决定在山水流淌的江中修筑如图1所示的“S”型圆弧堤坝．若堤坝的宽度忽略不计，图2中的两段圆弧半径都为57米，圆心角都为120°，则这“S”型圆弧堤坝的长为________米．(结果保留π)1176 π【点拨】[2022·黔东南州]如图，在△ABC中，∠A＝80°，半径为3 cm的⊙O是△ABC的内切圆，连接OB，OC，则图中阴影部分的面积是________cm2(结果用含π的式子表示)．12【点拨】根据∠A的度数和内切圆的性质，得出∠DOE的度数即可求出阴影部分的面积．中国魏晋时期的数学家刘徽首创“割圆术”，奠定了中国圆周率计算在世界上的领先地位．刘徽提出：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣．”由此求得圆周率π的近似值．133.11【点拨】正十二边形可分成12个如图所示的等腰三角形，其顶角为30°，即∠AOB＝30°.过点O作OH⊥AB于点H，则∠AOH＝15°.三、解答题(共48分)(12分)[2023·安庆一模]如图，圆锥侧面展开得到扇形，此扇形半径CA＝3，圆心角∠ACB＝120°，求此圆锥高OC的长度．14(12分)如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG＝CH，AG交BH于点P.15(1)求证：△ABG≌△BCH；(2)求∠APH的度数．【解】由(1)知△ABG≌△BCH，∴∠BAG＝∠HBC.∴∠APH＝∠ABP＋∠BAG＝∠ABP＋∠HBC＝∠ABC＝120°.(12分)如图，在Rt△AOB中，∠ABO＝90°，∠OAB＝30°，以点O为圆心，OB为半径的圆交BO的延长线于点C，过点C作OA的平行线，交⊙O于点D，连接AD.16(1)求证：AD为⊙O的切线；【证明】如图，连接OD.∵∠OAB＝30°，∠ABO＝90°，∴∠AOB＝60°.∵CD∥AO，∴∠C＝∠AOB＝60°.又∵OC＝OD，∴△COD是等边三角形．∴∠COD＝60°.∴∠AOD＝180°－60°－60°＝60°.∴∠AOB＝∠AOD.∵OB＝OD，AO＝AO，∴△AOB≌△AOD(SAS)．∴∠ADO＝∠ABO＝90°.又∵OD为⊙O的半径，∴AD为⊙O的切线．(2)若OB＝2，求弧CD的长．(12分) 如图，C是圆O被直径AB分成的半圆上一点，过点C的圆O的切线交AB的延长线于点P，连接CA，CO，CB.17(1)求证：∠ACO＝∠BCP；【证明】∵AB是半圆O的直径，∴∠ACB＝90°.∵CP是半圆O的切线，∴∠OCP＝90°.∴∠ACB＝∠OCP.∴∠ACO＝∠BCP.(2)若∠ABC＝2∠BCP，求∠P的度数；【解】由(1)知∠ACO＝∠BCP.∵∠ABC＝2∠BCP，∴∠ABC＝2∠ACO.∵OA＝OC，∴∠ACO＝∠A.∴∠ABC＝2∠A.∵∠ABC＋∠A＝90°，∴∠A＝30°，∠ABC＝60°.∴∠ACO＝∠BCP＝30°.∴∠P＝∠ABC－∠BCP＝60°－30°＝30°.(3)在(2)的条件下，若AB＝4，求图中阴影部分的面积(结果保留π和根号)．