24.2.1圆的基本性质 课件＋教案＋学案

导入新课

课件展示：

师：观察下列生活中的图片，找一找你所熟悉的图形.

生：圆

师：这节课，我们来学习圆的有关知识.

学生思考问题

引发学生思考，激发学生的学习兴趣

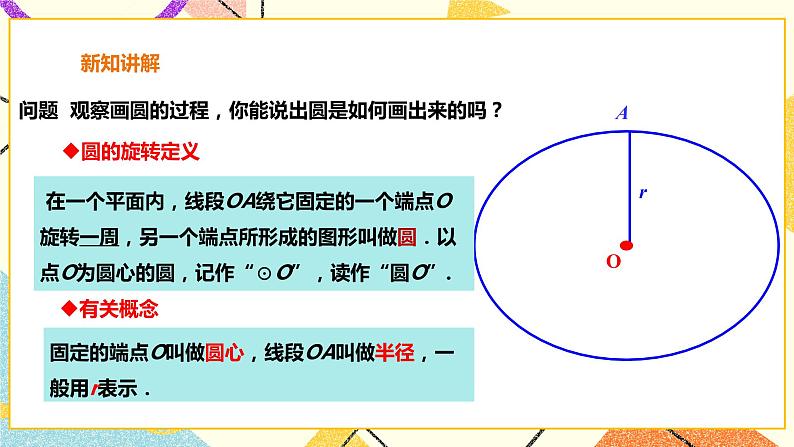
讲授新课

师：观察画圆的过程，你能说出圆是如何画出来的吗？

师：通过观察，你能给圆一个定义吗？

生：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点所形成的图形叫做圆．以点O为圆心的圆，记作“⊙O”，读作“圆O”.

师：思考，从画图的过程中，你能说出圆上的点有什么特性吗？

生：(1)圆上各点到定点(圆心O)的距离都等于定长(半径r)

(2) 到定点的距离都等于定长的点都在同一个圆上.

师：因此，圆可以被看成：平面内到定点（圆心O）的距离等于定长（半径）的所有点组成的图形。

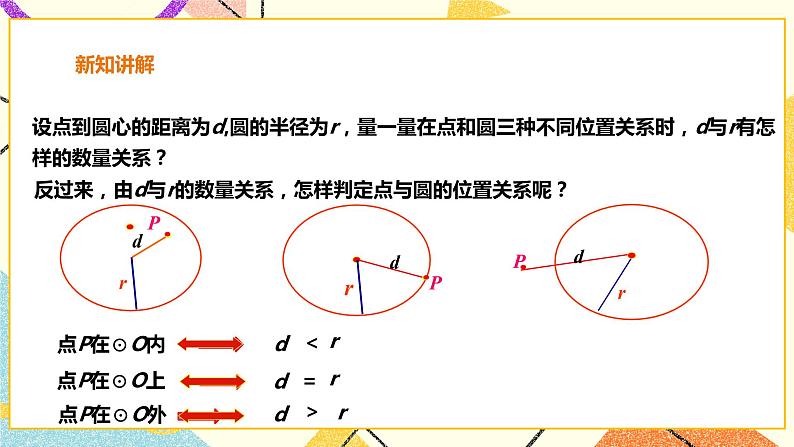
师：观察下图中点和圆的位置关系有哪几种？

生： 点与圆的位置关系有三种：点在圆内，点在圆上，点在圆外.

师：设点到圆心的距离为d,圆的半径为r，量一量在点和圆三种不同位置关系时，d与r有怎样的数量关系？

反过来，由d与r的数量关系，怎样判定点与圆的位置关系呢？

生： 点P在⊙O内         d<r

点P在⊙O上         d=r

点P在⊙O外         d>r

课件展示：

1.⊙O的半径为10cm，A、B、C三点到圆心的距离分别为8cm、10cm、12cm，则点A、B、C与⊙O的位置关系是：点A在        ；点B在        ；点C在       .                           

2.圆心为O的两个同心圆，半径分别为1和2，若OP= ，则点P在（       ）

A.大圆内         B.小圆内

C.小圆外          D.大圆内，小圆外

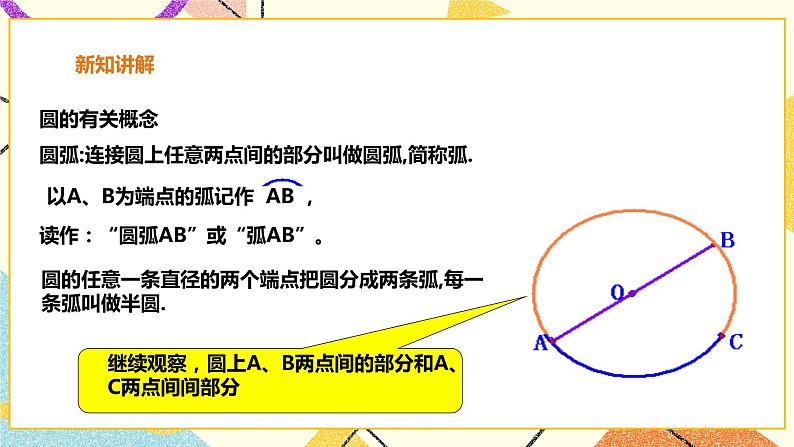
师： 请看圆的有关概念

圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.

圆的任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.

大于半圆的弧（用三个点表示，如： 或 ），叫做优弧；

小于半圆的弧叫做劣弧.  如:

弦：连接圆上任意两点的线段(图中的线段AB、AC）。

直径是经过圆心的弦（图中的AB）。

师：注意：凡直径都是弦,是圆中最长的弦,但弦不一定是直径.

师：再接着来学习

等弧:在同圆或等圆中，能够互相重合的弧叫做等弧.

弓形：由弦及其所对弧组成的图形叫做弓形。

师：长度相等的弧是等弧吗？

生：不是，必须在同圆或等圆中

课件展示：

例1.如图，AB、CD是⊙O的直径。

      求证：AD∥CD

学生在观察后，回答问题，然后教师讲解，总结出圆的定义。

学生动手画圆，教师及时展示学生练习结果，并及时给予点评，师生共同归纳圆上点的特征

学生在老师的指导下，观察，学生交流讨论并归纳出点与圆的位置关系

学生动手练习，教师及时展示学生练习结果，并及时给予点评.

学生观察思考后，总结圆的有关概念.

学生解答，教师及时展示学生练习结果，并及时给予点评.

通过观察，使学生形象、直观地理解圆的有关概念.

学生通过自己解决问题，充分发挥学习的主动性，同时也培养了学生归纳问题的能力。

培养学生独立思考，自己解决问题的能力

通过习题讲解，让学生加深对新知识的理解，培养学生分析问题和解决问题的能力.

课件演示及学生的动手操作，培养了学生观察能力和探究问题的能力、动手能力，以及与他人合作交流的能力，充分体现了教师为主导，学生为主体的教学思想，同时也突出了重点，突破难点.

通过例题讲解，让学生加深对新知识的理解，培养学生分析问题和解决问题的能力.

课堂练习

1.填空：

（1）_____是圆中最长的弦，它是______的2倍．

（2）图中有     条直径，     条非直径的弦，圆中以A为一个端点的优弧有     条，劣弧有      条．

答案：(1)直径，半径；(2)一、二、四、四

2.一点和⊙O上的最近点距离为4cm,最远的距离为10cm,则这个圆的半径是        。                     答案：7cm或3cm

3.判断下列说法的正误，并说明理由或举反例.

(1)弦是直径；

(2)半圆是弧；

(3)过圆心的线段是直径；

(4)过圆心的直线是直径；

(5)半圆是最长的弧；

(6)直径是最长的弦；

(7)长度相等的弧是等弧.
答案：(1)×；(2)√；(3)×；(4)×；(5)×；

(6)√；(7)×

4.正方形ABCD的边长为2cm，以A为圆心2cm为半径作⊙A，则点B在⊙A      ；点C在⊙A      ；点D在⊙A     .

 答案：上；外，上

5.如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（    ）

A．点P  B．点Q   C．点R    D．点M

答案：B

拓展提升

如图，已知 Rt△ABC 中 ，∠C=90°若 AC=12cm，BC=5cm，求的外接圆半径.

答案：

解：设Rt△ABC 的外接圆的外心为O，连接OC，OA=OB=OC.

∴O是斜边AB 的中点.

∵∠C=900，AC=12cm，BC=5cm.

∴AB=13cm，OA=6.5cm.

故Rt△ABC 的外接圆半径为6.5cm.

中考链接

1.[上海中考]小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是(      )

A.第①块   B.第②块  C.第③块   D.第④块

 答案：B

学生自主解答，教师讲解答案。

学生自主解答，教师讲解答案。

练中考题型

通过这几道题目来反馈学生对本节所学知识的掌握程度，落实基础。学生刚刚接触到新的知识需要一个过程，也就是对新知识从不熟悉到熟练的过程，无论是基础的习题，还是变式强化，都要以学生理解透彻为最终目标。

分层练习，可以照顾全体学生，让学有余力的学生有更大的进步.

让学生更早的接触中考题型，熟悉考点.

课堂小结

学生归纳本节所学知识

回顾学过的知识，总结本节内容，提高学生的归纳以及语言表达能力。

板书

圆的基本性质

1.在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点所形成的图形叫做圆

2.点与圆的位置关系有三种：点在圆内，点在圆上，点在圆外.

3.圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.

4.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.

5.连接圆上任意两点的线段叫弦，经过圆心的弦叫直径。

6.在同圆或等圆中，能够互相重合的弧叫做等弧.

7.由弦及其所对弧组成的图形叫做弓形