沪科版数学九年级下册24.3《圆周角》（ 第1课时）课件+教案

这是一份沪科版数学九年级下册24.3《圆周角》（ 第1课时）课件+教案，文件包含沪科版数学九年级下册243《圆周角》第1课时课件pptx、沪科版数学九年级下册243《圆周角》第1课时教案docx等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

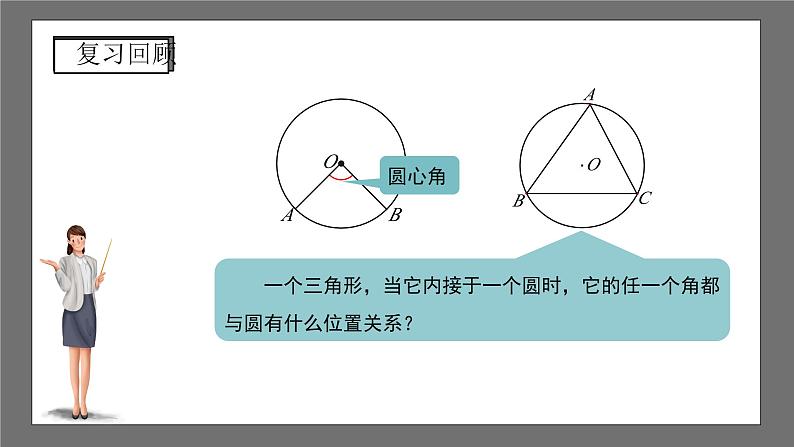
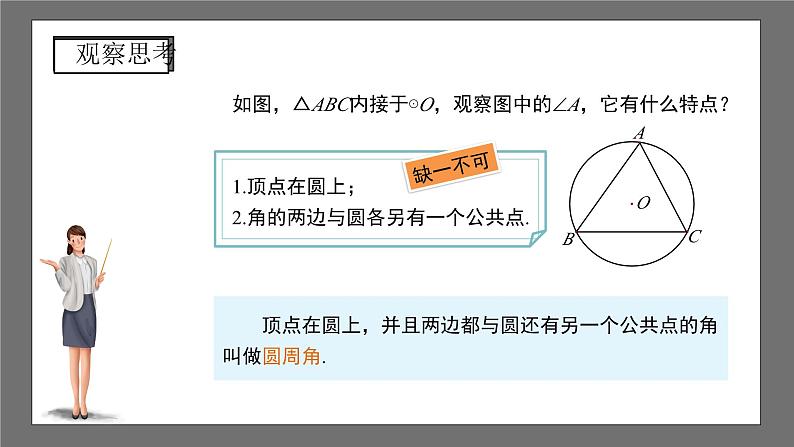
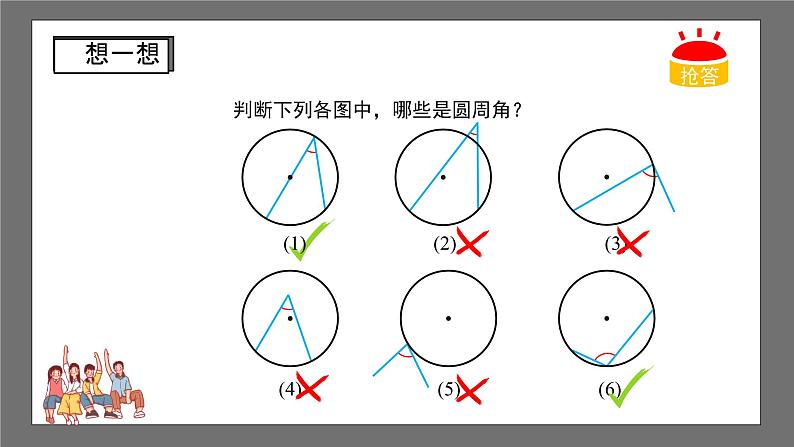
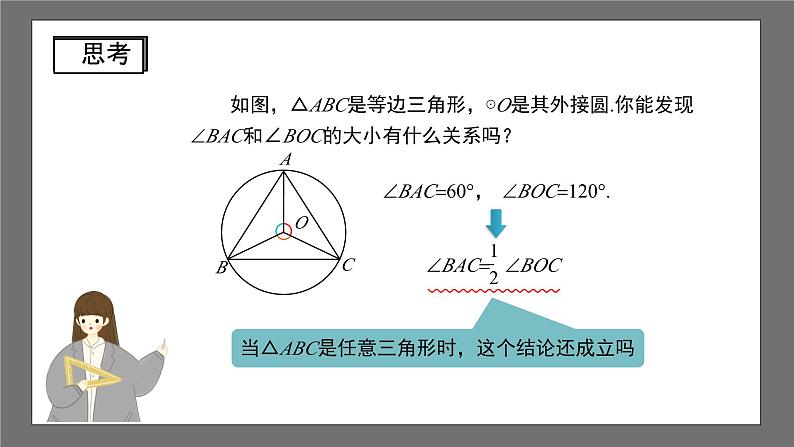
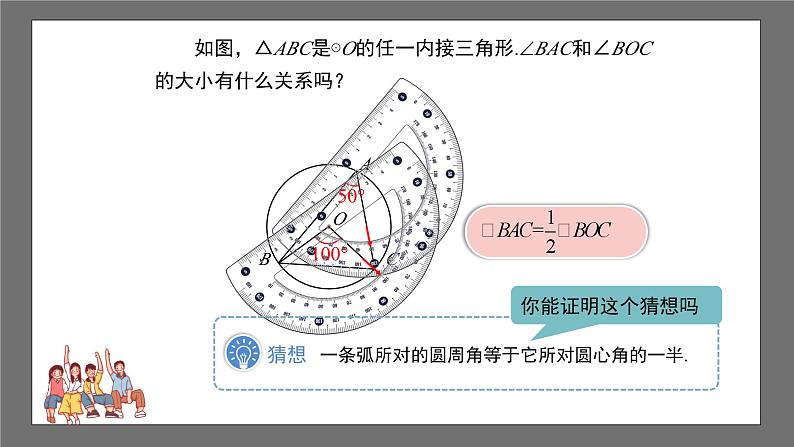
沪科版数学九年级下册24.3 圆周角第1课时 1.了解圆周角的概念； 2.掌握圆周角定理及其推论，并会熟练运用它们解决问题； 3.由圆周角与圆心角的关系的探索学会以特殊情形为基础，通过转化来解决一般问题的方法，并渗透分类的数学思想； 4.通过学生自主探究圆周角的概念及定理，合作交流的学习过程，体验实现自身价值的愉悦和数学的应用.如图，△ABC内接于⊙O，观察图中的A，它有什么特点？ 1.顶点在圆上；2.角的两边与圆各另有一个公共点.缺一不可判断下列各图中，哪些是圆周角？ 如图，△ABC是等边三角形，⊙O是其外接圆.你能发现BAC和∠BOC的大小有什么关系吗？BAC60°，BOC120°. 如图，△ABC是⊙O的任一内接三角形.BAC和∠BOC的大小有什么关系吗？100°50° 以⊙O上任一点A为顶点的圆周角有无数多个，按圆心与圆周角的位置关系，分为三种情况：1.圆心在圆周角的一边上，如图(1)；2.圆心在圆周角的内部，如图(2)；3.圆心在圆周角的外部，如图(3).OAOC∠A∠C∠BOC∠A∠CDD 如图，在⊙O中，BOC50°，求A的大小.解：由圆周角定理可得： “在同圆或等圆中，同弧所对的圆心角相等”那么同弧所对的圆周角呢？ “在同圆或等圆中，同弧所对的圆心角相等”那么同弧所对的圆周角呢？∠AC1B∠AC2B∠AC3BC2C1C3∠AC1B∠AC2B∠AC3B “在同圆或等圆中，同弧所对的圆心角相等”那么同弧所对的圆周角呢？∠ADC∠BAD∠AOC∠BOD 反过来，在同圆或等圆中，如果圆周角相等，那它们所对的弧相等吗？ADCBAD 如图，AB是直径，C是圆上任意一点(不与A、B重合)，求ACB °.90180°圆周角定理： 一条弧所对的圆周角等于它所对圆心角的一半.推论1：在同圆或等圆中，同弧或等弧所对的圆周角相等， 相等的圆周角所对的弧也相等.推论2：半圆(或直径)所对的圆周角是直角， 90°的圆周角所对的弦是直径. 例1 如图，AB为⊙O的直径，弦CD交AB于点P，ACD60°，ADC70°. 求∠APC的度数.OADCPB解：连接BC，则ACB90°，DCBACBACD90°60°30°.又∵BAD∠DCB30°，∴APCBADADC30°70°100°.APCBADADC70° ACBACD 1.如图，四边形ABCD的四个顶点在⊙O上，找出图中分别与1、2、3、4相等的角.解：1CBD； 2ACB； 3CAB； 4ABD. 2.如图AB是⊙O的直径，C，D是圆上的两点，若∠ABD=40°，则∠BCD=＿＿＿.50°AB是直径∠ADB90°∠BCD∠BAD∠ABD40°∠BAD50°50°40°3.已知：如图，OA，OB，OC都是⊙O的半径，AOB=2BOC. 求证：ACB2BAC.解：∵AOB2ACB， AOB=2BOC， ∴ACBBOC. ∵BOC=2BAC， ∴ACB2BAC. 4.证明：如果三角形一边上的中线等于该边的一半，那么这个三角形是直角三角形.证明：由题意得：OAOBOC. 即△ABC三个顶点都在以点O为圆心，OA的长为半径的圆上. ∵AC是⊙O的直径， 根据直径所对的圆周角是90°可得：ABC90°，即△ABC是直角三角形.教科书第31页习题24.3第1、2题课程结束