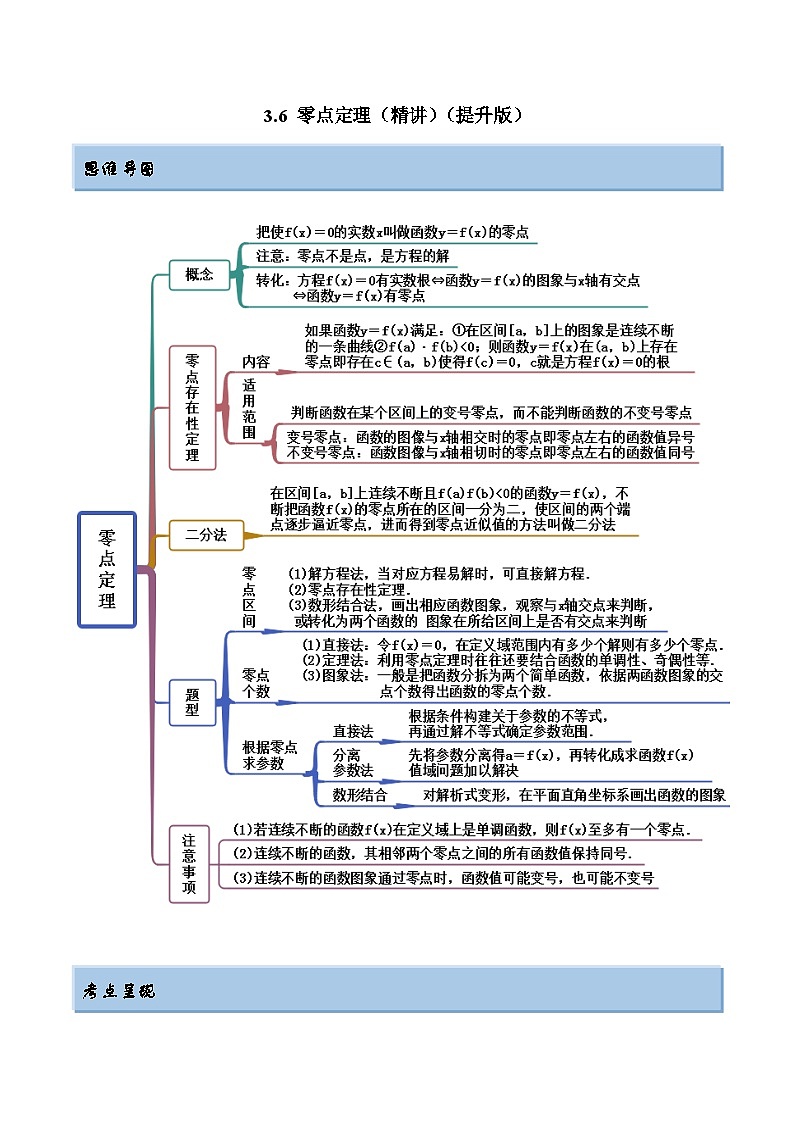
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.6 零点定理（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.6 零点定理（精讲）（提升版）（原卷版+解析版），共22页。试卷主要包含了零点的区间，零点的个数，比较零点的大小，已知零点求参数，零点的综合运用等内容，欢迎下载使用。


考点呈现
例题剖析
考点一 零点的区间
【例1】 (2023·河南开封·）函数的一个零点所在的区间是（ ）
A．B．C．D．
【一隅三反】
1． (2023·湖南）函数的零点所在区间是（ ）
A． B． C． D．
2． (2023·四川攀枝花）已知函数的零点在区间上，则（ ）
A．B．C．D．
3． (2023·云南德宏）方程的解所在的区间为（ ）
A．B．C．D．
考点二 零点的个数
【例2-1】 (2023·陕西）函数的零点个数为（ ）
A．0B．1C．2D．3
【例2-2】 (2023·山西）已知若，则在内的零点个数为（ ）
A．8B．9C．10D．11
【一隅三反】
1． (2023·安徽）已知函数则方程的解的个数是（ ）
A．0B．1C．2D．3
2． (2023·全国·高三专题练习）函数的图像与函数的图像的交点个数为（ ）
A．2B．3C．4D．0
3． (2023·海南省）设函数定义域为R，为奇函数，为偶函数，当时，，则函数有（ ）个零点
A．4B．5C．6D．7
考点三 比较零点的大小
【例3】 (2023·安徽）已知函数，，的零点分别为a，b，c则a，b，c的大小顺序为（ ）
A．B．
C．D．
【一隅三反】
1． (2023·河南）若实数满足，则（ ）
A．B．
C．D．
2． (2023·安徽）已知，，，则（ ）
A．B．C．D．
3． (2023·山西）正实数满足，则实数之间的大小关系为（ ）
A．B．C．D．
考点四 已知零点求参数
【例4-1】 (2023·山东潍坊）已知函数的图像与直线有3个不同的交点，则实数m的取值范围是（ ）
A．B．C．D．
【例4-2】 (2023·吉林）已知若关于x的方程有3个不同实根，则实数取值范围为（ ）
A．B．C．D．
【例4-3】 (2023·安徽·合肥市）已知函数在区间上有且仅有4个零点，则的取值范围是（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知函数若关于x的方程恰有三个不相等的实数解，则m的取值范围是（ ）
A．B．
C．D．
2． (2023·河南·模拟预测（理））已知函数为定义在上的单调函数，且．若函数有3个零点，则的取值范围为（ ）
A．B．
C．D．
3． (2023·广西·贵港市高级中学三模）已知在有且仅有6个实数根，则实数的取值范围为（ ）
A．B．
C．D．
4． (2023·山西）已知函数，若函数恰好有两个零点，则实数k的取值范围是（ ）
A．B．C．D．
考点五 零点的综合运用
【例5-1】 (2023·新疆克拉玛依）函数在区间上的所有零点之和为（ ）
A．B．
C．D．
【例5-2】 (2023·甘肃）若函数在区间上有2个零点，则的取值范围是（ ）
A．B．C．D．
【例5-3】 (2023·全国·高三专题练习）已知函数的零点为，函数的零点为，则下列不等式中成立的是（ ）
A．B．
C．D．
【一隅三反】
1． (2023·安徽·合肥一六八中学）若为奇函数，且是的一个零点，则一定是下列哪个函数的零点（ ）
A．B．C．D．
2． (2023·陕西·模拟预测（理））已知 是方程的根， 是方程的根，则的值为（ ）
A．2B．3C．6D．10
3． (2023·陕西·西安中学一模（理））函数的所有零点之和为_________.
3.6 零点定理（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 零点的区间
【例1】 (2023·河南开封·）函数的一个零点所在的区间是（ ）
A．B．C．D．
【答案】D
【解析】因为，的定义域为，
，所以在上单调递增，
所以，，
由零点存在性定理知：，函数的一个零点所在的区间是.故选：D.
【一隅三反】
1． (2023·湖南）函数的零点所在区间是（ ）
A． B． C． D．
【答案】B
【解析】因为是上的增函数，且，所以的零点在区间内.
故选：B
2． (2023·四川攀枝花）已知函数的零点在区间上，则（ ）
A．B．C．D．
【答案】C
【解析】函数的定义域为，且在上单调递增，故其至多一个零点；
又，，故的零点在区间，故.故选：．
3． (2023·云南德宏）方程的解所在的区间为（ ）
A．B．C．D．
【答案】B
【解析】设，易知在定义域内是增函数，
又，，所以的零点在上，即题中方程的根属于．故选：B．
考点二 零点的个数
【例2-1】 (2023·陕西）函数的零点个数为（ ）
A．0B．1C．2D．3
【答案】D
【解析】当时，则函数的零点个数为函数与函数，的交点个数作出两个函数的图象如下图所示，
由图可知，当时，函数的零点有两个，
当时，，即当时，函数的零点有一个.
综上，函数的零点有三个.故选：D
【例2-2】 (2023·山西）已知若，则在内的零点个数为（ ）
A．8B．9C．10D．11
【答案】B
【解析】作出的图像，则在内的零点个数为曲线
与直线在内的交点个数9.
选：B.
【一隅三反】
1． (2023·安徽）已知函数则方程的解的个数是（ ）
A．0B．1C．2D．3
【答案】C
【解析】令，得，则函数零点的个数即函数与函数的交点个数．作出函数与函数的图像，可知两个函数图像的交点的个数为2，故方程的解的个数为2个．故选：C．
2． (2023·全国·高三专题练习）函数的图像与函数的图像的交点个数为（ ）
A．2B．3C．4D．0
【答案】C
【解析】在上是增函数，在和上是减函数，在和上是增函数，，，，
作出函数的图像，如图，由图像可知它们有4个交点．
故选：C．
3． (2023·海南省）设函数定义域为R，为奇函数，为偶函数，当时，，则函数有（ ）个零点
A．4B．5C．6D．7
【答案】C
【解析】的零点个数即的图象交点个数.因为为奇函数，故关于原点对称，故关于对称，又为偶函数，故关于对称，又当时，，画出图象，易得函数的图象有6个交点
故选：C
考点三 比较零点的大小
【例3】 (2023·安徽）已知函数，，的零点分别为a，b，c则a，b，c的大小顺序为（ ）
A．B．
C．D．
【答案】D
【解析】由得，，
由得，由得.
在同一平面直角坐标系中画出、、的图象，
由图象知，，.
故选：D
【一隅三反】
1． (2023·河南）若实数满足，则（ ）
A．B．
C．D．
【答案】B
【解析】画出与三个函数的图象，如图可得的与交点的横坐标依次为，故
故选：B
2． (2023·安徽）已知，，，则（ ）
A．B．C．D．
【答案】A
【解析】设函数，易知在上递增，
，，即，由零点存在定理可知．；
设函数，易知在上递增，，，即，由零点存在定理可知，；
设函数，易知在上递减，，，因为，由函数单调性可知，，即.故选:A．
3． (2023·山西）正实数满足，则实数之间的大小关系为（ ）
A．B．C．D．
【答案】A
【解析】，即，即，与的图象在只有一个交点，
则在只有一个根，令，
，，，则；
，即，即，由与的图象在只有一个交点，
则在只有一个根，令，，
，，故；
，即，
即，由与的图象在只有一个交点，
则在只有一个根，令，，
，，则；故选：A.
考点四 已知零点求参数
【例4-1】 (2023·山东潍坊）已知函数的图像与直线有3个不同的交点，则实数m的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】对函数求导得：，
当或时，，当时，，即在，上单调递增，在上单调递减，
在处取得极大值，在处取得极小值，
在同一坐标系内作出函数的图像和直线，如图，
观察图象知，当时，函数的图像与直线有3个不同的交点，
所以实数m的取值范围是.故选：B
【例4-2】 (2023·吉林）已知若关于x的方程有3个不同实根，则实数取值范围为（ ）
A．B．C．D．
【答案】D
【解析】因为时，，则，令，则，所以时，，则单调递增；时，，则单调递减；且，，时，；
时，，则，令，则，所以时，，则单调递增；时，，则单调递减；且，，时，；
作出在上的图象，如图：
由图可知要使有3个不同的实根，则.
故选：D.
【例4-3】 (2023·安徽·合肥市）已知函数在区间上有且仅有4个零点，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】根据题意，函数，
若，即，必有，令，则，
设，则函数和在区间内有4个交点，
又由于，必有，即的取值范围是，故选：B.
【一隅三反】
1． (2023·全国·高三专题练习）已知函数若关于x的方程恰有三个不相等的实数解，则m的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】函数的图像如下图所示：
若关于x的方程恰有三个不相等的实数解，
则函数的图像与直线有三个交点，
若直线经过原点时，m＝0，
若直线与函数的图像相切，令，令.故.故选：D．
2． (2023·河南·模拟预测（理））已知函数为定义在上的单调函数，且．若函数有3个零点，则的取值范围为（ ）
A．B．
C．D．
【答案】A
【解析】因为为定义在R上的单调函数，所以存在唯一的，使得，
则，，即，
因为函数为增函数，且，所以，.
当时，由，得；当时，由，得.
结合函数的图象可知，若有3个零点，则．
故选：A
3． (2023·广西·贵港市高级中学三模）已知在有且仅有6个实数根，则实数的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】由，得，即.
设，即在有且仅有6个实数根，
因为，故只需，解得，故选：D．
4． (2023·山西）已知函数，若函数恰好有两个零点，则实数k的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】由题意知，画出函数的简图，如图所示
由恰好有两个零点转化为与直线有两个不同的交点，
由图知，当直线经过点两点的斜率为，则.
所以实数k的取值范围为.故选：C.
考点五 零点的综合运用
【例5-1】 (2023·新疆克拉玛依）函数在区间上的所有零点之和为（ ）
A．B．
C．D．
【答案】C
【解析】因为，令，即，当时显然不成立，
当时，作出和的图象，如图，
它们关于点对称，
由图象可知它们在上有4个交点，且关于点对称，每对称的两个点的横坐标和为，所以4个点的横坐标之和为．故选：C．
【例5-2】 (2023·甘肃）若函数在区间上有2个零点，则的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】函数在区间上有2个零点
即方程在区间上有2个实数根
设，则为偶函数.且
当时，，当时，在上单调递增，且
所以在上单调递减，则在上单调递增，
又时，；时，，则的大致图像如图.
所以方程在区间上有2个实数根满足
则，设，则在上恒成立
所以
故选：A
【例5-3】 (2023·全国·高三专题练习）已知函数的零点为，函数的零点为，则下列不等式中成立的是（ ）
A．B．
C．D．
【答案】C
【解析】令、，则、，
在同一坐标系中分别绘出函数、、的图像，
因为函数的零点为，函数的零点为，所以，，
解方程组，
因为函数与互为反函数，所以由反函数性质知、关于对称，
则，，，A、B、D错误，
因为，所以在上单调递增，因为，，
所以，因为点在直线上，
所以，，故C正确，
故选：C．
【一隅三反】
1． (2023·安徽·合肥一六八中学）若为奇函数，且是的一个零点，则一定是下列哪个函数的零点（ ）
A．B．C．D．
【答案】B
【解析】是奇函数，且是的一个零点，
所以，把分别代入下面四个选项，
对于A，，不一定为0，故A错误；
对于B，，所以是函数的零点，故B正确；
对于C，，故C不正确；
对于D，，故D不正确；
故选：B.
2． (2023·陕西·模拟预测（理））已知 是方程的根， 是方程的根，则的值为（ ）
A．2B．3C．6D．10
【答案】A
【解析】方程可变形为方程，方程可变形为方程，
是方程的根，是方程的根，
是函数与函数的交点横坐标，是函数与函数的交点横坐标，
函数与函数互为反函数，
函数与函数的交点横坐标等于函数与函数的交点纵坐标,即在数图象上，
又图象上点的横纵坐标之积为2， ，
故选：．
3． (2023·陕西·西安中学一模（理））函数的所有零点之和为_________.
【答案】
【解析】由，可得，令，
可得函数与的图象都关于直线的对称，
在同一坐标系内作出函数与的图象，如图所示，
由图象可得，函数与的图象有6个公共点，
其横坐标依次为，
这6个点两两关于直线的对称，所以，
所以，
即函数的所有零点之和为.
故答案为：.