2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.1 切线方程（精练）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.1 切线方程（精练）（提升版）（原卷版+解析版），共40页。试卷主要包含了切线与其他知识的运用等内容，欢迎下载使用。

1． (2023·河南·南阳中学）设函数满足，则（ ）
A．B．1C．D．2
2． (2023·山东）（多选）设点P是曲线上的任意一点，P点处的切线的倾斜角为，则角的取值范围包含（ ）
A． B． C． D．
3． (2023·河南·郑州市第二高级中学）设点是函数图象上的任意一点，点处切线的倾斜角为，则角的取值范围是（ ）
A．B．
C．D．
4． (2023·全国·高三专题练习）已知，则曲线在点处的切线的斜率为（ ）
A．B．C．D．
5． (2023·广东·佛山一中）已知点是曲线上一动点，当曲线在处的切线斜率取得最小值时，该切线的倾斜角为（ ）
A．B．C．D．
6． (2023·全国·高三专题练习）已知函数是定义在R上的奇函数，且，则函数的图象在点处的切线的斜率为（ ）
A．B．C．D．
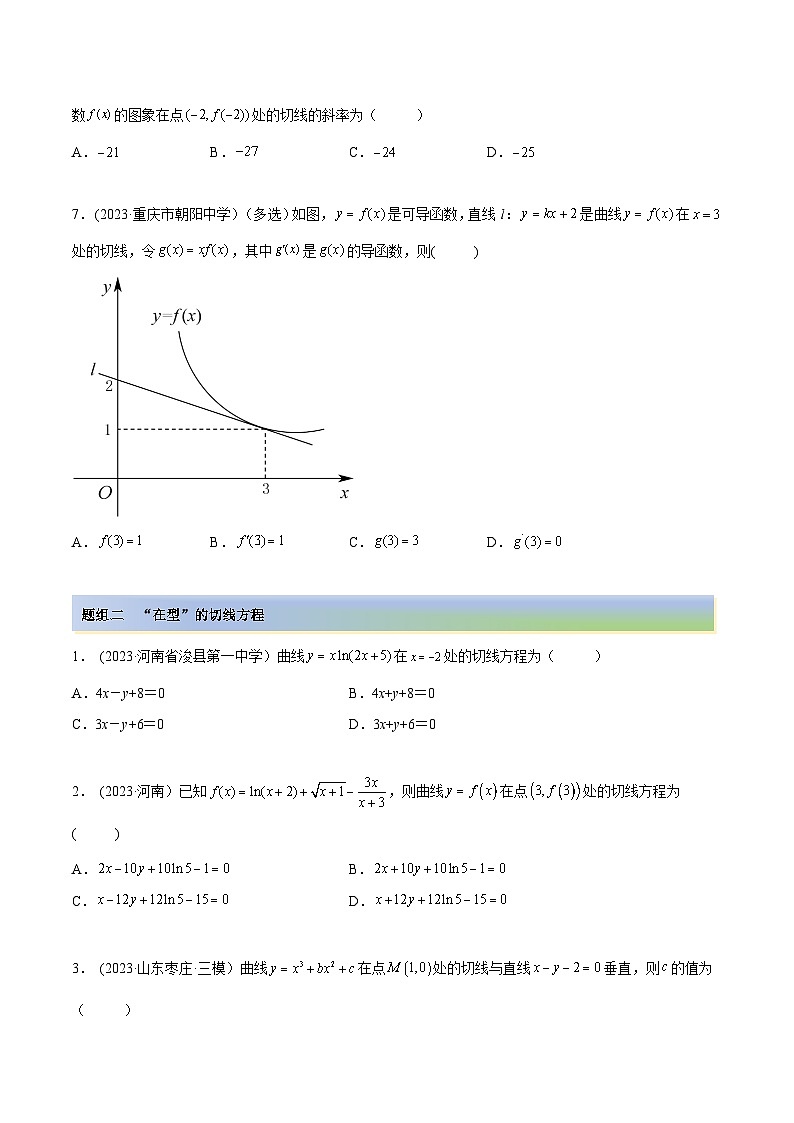
7． (2023·重庆市朝阳中学）（多选）如图，是可导函数，直线 l：是曲线在处的切线，令，其中是的导函数，则( )
A．B．C．D．
题组二 “在型”的切线方程
1． (2023·河南省浚县第一中学）曲线在处的切线方程为（ ）
A．4x－y+8＝0B．4x+y+8＝0
C．3x－y+6＝0D．3x+y+6＝0
2． (2023·河南）已知，则曲线在点处的切线方程为( )
A．B．
C．D．
3． (2023·山东枣庄·三模）曲线在点处的切线与直线垂直，则的值为（ ）
A．B．C．D．
4． (2023·江苏苏州·模拟预测）已知奇函数在点处的切线方程为，则（ ）
A．或1B．或C．或2D．或
5． (2023·安徽·蚌埠二中）已知定义域为的函数存在导函数，且满足，则曲线在点处的切线方程可能是（ ）
A．B．C．D．
6． (2023·河南·南阳中学）若直线与曲线相切，直线与曲线相切，则的值为（ ）
A．B．1C．eD．
7． (2023·江苏连云港）（多选）已知，直线与曲线相切，则下列不等式一定成立的是（ ）
A．B．C．D．
8． (2023·安徽·蒙城第一中学）已知为奇函数，且当时，，则曲线在点处的切线方程为__________.
9． (2023·云南·一模）若曲线在点处的切线与直线平行，则__________.
10． (2023·全国·高三专题练习）若曲线在点处的切线与曲线相切于点，则__________.
题组三 “过型”的切线方程
1． (2023·广东茂名）已知直线l为函数的切线，且经过原点，则直线l的方程为__________.
2． (2023·四川成都）已知函数f（x）= x3－3x，则过点（1，－2）的切线方程为__________．
3． (2023·四川成都）过点的直线l与曲线相切，则直线l的斜率为___________.
4． (2023·广东·南海中学）函数过原点的切线方程是_______.
题组五 切线或切点的数量
1． (2023·山东泰安）过曲线外一点作的切线恰有两条，则（ ）
A．B．C．D．
2． (2023·内蒙古呼和浩特）若过点可以作三条直线与曲线C：相切，则m的取值范围是（ ）
A．B．C．D．
3． (2023·重庆·二模）已知曲线及点，则过点且与曲线相切的直线可能有（ ）
A．0条B．1条C．2条D．3条
4． (2023·福建漳州·二模）（多选）已知函数，则下列结论正确的是（ ）
A．曲线的切线斜率可以是1
B．曲线的切线斜率可以是
C．过点且与曲线相切的直线有且只有1条
D．过点且与曲线相切的直线有且只有2条
5． (2023·山东潍坊·三模）过点有条直线与函数的图像相切，当取最大值时，的取值范围为（ ）
A．B．C．D．
6． (2023·全国·模拟预测（理））过点作曲线的切线，当时，切线的条数是（ ）
A．B．C．D．
7． (2023·全国·高三专题练习）若过点可以作曲线的两条切线，则（ ）
A．B．C．D．
8． (2023·山东·菏泽一中高二阶段练习）若直线与曲线和都相切，则直线的条数有（ ）
A．B．C．D．无数条
9． (2023·重庆市育才中学高三阶段练习）若直线（）为曲线与曲线的公切线，则l的纵截距（ ）
A．0B．1C．eD．
10． (2023·全国·高考真题）若过点可以作曲线的两条切线，则（ ）
A．B．
C．D．
11． (2023·河北·高三阶段练习）若过点可以作三条直线与曲线相切，则m的取值范围为（ ）
A．B．C．D．
12． (2023·广东深圳·二模）已知，若过点可以作曲线的三条切线，则（ ）
A．B．C．D．
13． (2023·辽宁·辽师大附中）已知过点P(0，a)可作出曲线y=2x3–3x2的3条不同的切线，则实数a的取值范围是_______________ .
14． (2023·陕西·长安一中）已知函数，若过点存在三条直线与曲线相切，则的取值范围为___________．
15． (2023·安徽蚌埠）已知函数，过点作曲线的切线，则可作切线的最多条数是______．
题组五 公切线
1． (2023·海南）已知存在，使得函数与的图象存在相同的切线，且切线的斜率为1，则b的最大值为___.
2． (2023·安徽·安庆一中）若直线是曲线的切线，切点为，也是曲线的切线，切点为，则__________．
3． (2023·山东威海·三模）已知曲线，若有且只有一条直线同时与，都相切，则________．
4． (2023·江西萍乡·三模（文））若存在实数，使得函数与的图象有相同的切线，且相同切线的斜率为，则实数的最大值为_________．
5． (2023·山东师范大学附中模拟预测）已知函数，若存在一条直线同时与两个函数图象相切，则实数a的取值范围__________．
6． (2023·安徽·合肥市第八中学模拟预测（理））若曲线与曲线存在2条公共切线，则a的值是_________．
题组六 切线与其他知识的运用
1． (2023·湖南·株洲二中）已知，，直线与曲线相切，则的最小值是（ ）
A．B．C．D．
2． (2023·江苏·苏州市苏州高新区第一中学）直线 分别与曲线， 直线 交于 两点， 则 的最小值为（ ）
A．B．C．D．
3． (2023·广西·高三阶段练习）在平面直角坐标系中，是直线与曲线在第一象限的交点，是直线上的一点，且满足.为曲线上动点，当取最小值时，的横坐标为（ ）
A．B．C．D．
4． (2023·重庆市第十一中学校）二次函数的图象在点处的切线与轴交点的横坐标为，为正整数，，若数列的前项和为，则（ ）
A．B．C．D．
5． (2023·四川·石室中学二模（理））已知函数在x=0处的切线与直线平行，则二项式展开式中含项的系数为（ ）
A．26B．46C．36D．56
6． (2023·云南保山）已知曲线在点处的切线为l，数列的首项为1，点为切线l上一点，则数列中的最小项为（ ）
A．B．C．D．
7． (2023·湖南·模拟预测）已知抛物线，P为直线上一点，过P作抛物线的两条切线，切点分别为A，B，则的最小值为（ ）
A．B．-1C．D．-2
8． (2023·湖北·襄阳五中二模）已知函数在x=0处的切线与直线平行，则二项式展开式中含项的系数为_________．
题组七 切线方程的运用
1． (2023·广西·柳州市第三中学）曲线上的点到直线的距离的最小值为（ ）
A．B．
C．D．
2． (2023·江苏省太湖高级中学）若点P是曲线上任一点，则点P到直线的最小距离是（ ）
A．B．C．D．
3． (2023·山东·德州市教育科学研究院）已知函数，，若有两个零点，则k的取值范围为（ ）
A．B．C．D．
4． (2023·辽宁·沈阳二十中）若x、a、b为任意实数，若，则最小值为( )
A．B．9C．D．
5 (2023·河北保定）若函数有两个极值点，则实数a的取值范围为（ ）
A．B．C．D．
6． (2023·山西·灵丘县第一中学校）已知函数若直线与有三个不同的交点，则实数的取值范围是（ ）
A．B．C．D．
7． (2023·全国·高三专题练习（理））若点与曲线上点距离最小值为，则实数为_______.
8． (2023·河北邯郸·二模）已知点P为曲线上的动点，O为坐标原点．当最小时，直线OP恰好与曲线相切，则实数a＝___．
9． (2023·全国·高三专题练习）已知实数、、、满足，则的最小值为______．
4.1 切线方程（精练）（提升版）
题组一 斜率与倾斜角
1． (2023·河南·南阳中学）设函数满足，则（ ）
A．B．1C．D．2
【答案】A
【解析】因为，，，
所以，故选：A
2． (2023·山东）（多选）设点P是曲线上的任意一点，P点处的切线的倾斜角为，则角的取值范围包含（ ）
A． B． C． D．
【答案】CD
【解析】，，依题意：，，
∵倾斜角的取值范围是，∴，故选：CD.
3． (2023·河南·郑州市第二高级中学）设点是函数图象上的任意一点，点处切线的倾斜角为，则角的取值范围是（ ）
A．B．
C．D．
【答案】B
【解析】，，，，，.
点P是曲线上的任意一点，点P处切线的倾斜角为，.
，.故选：B.
4． (2023·全国·高三专题练习）已知，则曲线在点处的切线的斜率为（ ）
A．B．C．D．
【答案】D
【解析】对，
求导可得，，得到，所以，
，所以，，
故选D
5． (2023·广东·佛山一中）已知点是曲线上一动点，当曲线在处的切线斜率取得最小值时，该切线的倾斜角为（ ）
A．B．C．D．
【答案】D
【解析】根据题意得，，所以，当且仅当时成立，所以该切线的倾斜角为：.故选：D.
6． (2023·全国·高三专题练习）已知函数是定义在R上的奇函数，且，则函数的图象在点处的切线的斜率为（ ）
A．B．C．D．
【答案】A
【解析】是奇函数，
恒成立，所以，
，，所以，，即，
．故选：A．
7． (2023·重庆市朝阳中学）（多选）如图，是可导函数，直线 l：是曲线在处的切线，令，其中是的导函数，则( )
A．B．C．D．
【答案】ACD
【解析】由图可知，f(3)＝1，故A正确；
(3，1)在y＝kx＋2上，故1＝3k＋2，故，故B错误；
，则，故C正确；
，，故D正确.故选：ACD.
题组二 “在型”的切线方程
1． (2023·河南省浚县第一中学）曲线在处的切线方程为（ ）
A．4x－y+8＝0B．4x+y+8＝0
C．3x－y+6＝0D．3x+y+6＝0
【答案】B
【解析】因为，所以，所以．
又当时，，故切点坐标为，所以切线方程为．故选：B.
2． (2023·河南）已知，则曲线在点处的切线方程为( )
A．B．
C．D．
【答案】A
【解析】∵，∴，
，∴，
∴y=f(x)在处的切线方程为：，即．故选：A．
3． (2023·山东枣庄·三模）曲线在点处的切线与直线垂直，则的值为（ ）
A．B．C．D．
【答案】C
【解析】设，则，直线的斜率为，
由题意可得，解得.故选：C.
4． (2023·江苏苏州·模拟预测）已知奇函数在点处的切线方程为，则（ ）
A．或1B．或C．或2D．或
【答案】D
【解析】由可得，
因为，所以，解得.所以，故切线斜率，
又，所以，解得或，
所以或.故选：D
5． (2023·安徽·蚌埠二中）已知定义域为的函数存在导函数，且满足，则曲线在点处的切线方程可能是（ ）
A．B．C．D．
【答案】B
【解析】的定义域为，由可知，是偶函数，
由可知，周期为4，
因为，故关于轴对称，
又因为，所以也是的对称轴，
因为在上存在导函数，所以是的极值点，
即，曲线在点处的切线斜率为0，故切线方程可能为.故选：B.
6． (2023·河南·南阳中学）若直线与曲线相切，直线与曲线相切，则的值为（ ）
A．B．1C．eD．
【答案】B
【解析】设直线与曲线相切于点，
直线与曲线相切于点，则，且，所以，
，且，所以，
令，，
当时，，单调递减，
当时，，单调递增，
且，，所以当时，，
因为，，即，所以，
所以，故故选：B
7． (2023·江苏连云港）（多选）已知，直线与曲线相切，则下列不等式一定成立的是（ ）
A．B．C．D．
【答案】BCD
【解析】设切点为，因为，所以，得，所以，所以，
对于 A，，所以，当且仅当时，等号成立，故A不正确；
对于B，，当且仅当时，等号成立，故B正确；
对于C，，当且仅当，时，等号成立，故C正确；对于D，，
所以 ，当且仅当，又，即时，等号成立.故选：BCD
8． (2023·安徽·蒙城第一中学）已知为奇函数，且当时，，则曲线在点处的切线方程为__________.
【答案】
【解析】因为为奇函数，且当时，，
当时，，
则，所以且，
故切线方程为，即.故答案为：
9． (2023·云南·一模）若曲线在点处的切线与直线平行，则__________.
【答案】
【解析】由题意知，令，则
，，
，
所以点在曲线上，
，
，
，，
，
所以，
又曲线在点处的切线与直线平行，
所以，得.
故答案为：.
10． (2023·全国·高三专题练习）若曲线在点处的切线与曲线相切于点，则__________.
【答案】
【解析】的导数为，可得曲线在点处的切线方程为，
的导数为，可得曲线在点处的切线的方程为，
由两条切线重合的条件，可得，且，
则，即有，
可得，则.故答案为:
题组三 “过型”的切线方程
1． (2023·广东茂名）已知直线l为函数的切线，且经过原点，则直线l的方程为__________.
【答案】
【解析】设切点坐标为，所以直线l的斜率为，
所以直线l的方程为
又直线l过点，所以，整理得，解得，
所以，直线l的斜率，所以直线l的方程为，故答案为：.
2． (2023·四川成都）已知函数f（x）= x3－3x，则过点（1，－2）的切线方程为__________．
【答案】和
【解析】由函数，则，
当点为切点时，则，即切线的斜率， 所以切线的方程为，
当点不是切点时，设切点，则，即，
解得或（舍去），所以所以切线的方程为，即．
故答案为：和．
3． (2023·四川成都）过点的直线l与曲线相切，则直线l的斜率为___________.
【答案】3或
【解析】因为，所以，，
当为切点时，，
当不为切点时，设切点为，，
所以，
所以切线方程为：，
过点，所以
即，即，解得或（舍），
所以切点为，所以，综上所述：直线l的斜率为3或，故答案为：3或
4． (2023·广东·南海中学）函数过原点的切线方程是_______.
【答案】.
【解析】设切点为，，则，
故切点为的切线方程为，
又因此切线过原点，所以，解得，
所以函数过原点的切线方程是，即.故答案为：.
题组五 切线或切点的数量
1． (2023·山东泰安）过曲线外一点作的切线恰有两条，则（ ）
A．B．C．D．
【答案】A
【解析】，过点作曲线C的切线，
设切点，则切线方程为：，
将代入得：
即（*） 由条件切线恰有两条，方程（*）恰有两根．
令，，
显然有两个极值点与，于是或当时，；
当时，，此时经过与条件不符，所以，
故选：A.
2． (2023·内蒙古呼和浩特）若过点可以作三条直线与曲线C：相切，则m的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】设切点为,过点P的切线方程为,代入点P坐标，化简为，即这个方程有三个不等根即可.
令,求导得：.
令，解得：，所以在上递增；令，解得：或，所以在和上递增.
要使方程有三个不等根即可.
只需,即.
故选：D
3． (2023·重庆·二模）已知曲线及点，则过点且与曲线相切的直线可能有（ ）
A．0条B．1条C．2条D．3条
【答案】BC
【解析】因为，所以，
设切点， 在点处的导数为，
根据导数的几何意义等于切线斜率，以及导数的比值定义式有：
整理得 ，所以，
①当时，可化为，由函数定义域知分母不为0，，
所以只能解得，因此过只能找到一条与曲线相切的直线；
②当时，可化为，
是关于的二次方程，，且两根之积为，
所以所求根之中一定不含0，此时对任意能够找到两个满足条件.
综上所述，过点且与曲线相切的直线可能有1或2条.故选：BC.
4． (2023·福建漳州·二模）（多选）已知函数，则下列结论正确的是（ ）
A．曲线的切线斜率可以是1
B．曲线的切线斜率可以是
C．过点且与曲线相切的直线有且只有1条
D．过点且与曲线相切的直线有且只有2条
【答案】AC
【解析】因为函数，所以
A.令，得 ，所以曲线的切线斜率可以是1，故正确；
B.令无解，所以曲线的切线斜率不可以是，故错误；
C. 因为在曲线上，所以点是切点，则，
所以切线方程为，即，所以过点且与曲线相切的直线有且只有1条，故正确；
D.设切点，则切线方程为，因为点在切线上，所以，解得，所以过点且与曲线相切的直线有且只有1条，故错误；
故选：AC
5． (2023·山东潍坊·三模）过点有条直线与函数的图像相切，当取最大值时，的取值范围为（ ）
A．B．C．D．
【答案】B
【解析】由，，故当时，，单调递减，且；当时，，单调递增，结合图象易得，过点至多有3条直线与函数的图像相切，故.
此时，设切点坐标为，则切线斜率，所以切线方程为，将代入得，存在三条切线即函数有三个不同的根，又，易得在上，，单调递增；在和上，，单调递减，画出图象可得当，即时符合题意
故选：B
6． (2023·全国·模拟预测（理））过点作曲线的切线，当时，切线的条数是（ ）
A．B．C．D．
【答案】D
【解析】设切点为，
，切线斜率，
切线方程为：；
又切线过，；
设，则，
当时，；当时，；
在，上单调递减，在上单调递增，
又，，恒成立，可得图象如下图所示，
则当时，与有三个不同的交点，
即当时，方程有三个不同的解，切线的条数为条.
故选：D.
7． (2023·全国·高三专题练习）若过点可以作曲线的两条切线，则（ ）
A．B．C．D．
【答案】D
【解析】
设切点坐标为，由于，因此切线方程为，又切线过点，则，，
设，函数定义域是，则直线与曲线有两个不同的交点，，
当时，恒成立，在定义域内单调递增，不合题意；当时，时，，单调递减，
时，，单调递增，所以，结合图像知，即.
故选：D.
8． (2023·山东·菏泽一中高二阶段练习）若直线与曲线和都相切，则直线的条数有（ ）
A．B．C．D．无数条
【答案】C
【解析】设直线因为直线与曲线和都相切
所以对于曲线，，，切点
对于曲线，，，切点
因为公切线过A、B两点
所以
进而可得
令

因为，均为增函数，又因为，
所以存在使得即
所以在时单调递减，在单调递增，
又因为
所以
当时，
因为，所以所以在内存在使得直线与曲线和都相切
当时，
因为，所以所以在内存在使得直线与曲线和都相切
所以综上所述，存在两条斜率分别为的两条直线与曲线和都相切
故选：C
9． (2023·重庆市育才中学高三阶段练习）若直线（）为曲线与曲线的公切线，则l的纵截距（ ）
A．0B．1C．eD．
【答案】D
【解析】设l与的切点为，则由，有.
同理，设l与的切点为，由，有.
故 解得 或 则或.
因，所以l为时不成立.故，
故选：D.
10． (2023·全国·高考真题）若过点可以作曲线的两条切线，则（ ）
A．B．
C．D．
【答案】D
【解析】在曲线上任取一点，对函数求导得，
所以，曲线在点处的切线方程为，即，
由题意可知，点在直线上，可得，
令，则.
当时，，此时函数单调递增，
当时，，此时函数单调递减，
所以，，
由题意可知，直线与曲线的图象有两个交点，则，
当时，，当时，，作出函数的图象如下图所示：
由图可知，当时，直线与曲线的图象有两个交点.
故选：D.
解法二：画出函数曲线的图象如图所示，根据直观即可判定点在曲线下方和轴上方时才可以作出两条切线.由此可知.
故选：D.
11． (2023·河北·高三阶段练习）若过点可以作三条直线与曲线相切，则m的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】由，则，设切点为，则切线斜率
则在点的切线方程为，
代入点P坐标得
整理为，即这个方程有三个不等式实根，
令，则 ，
令则
函数在上单调递减，在上单调递增，在上单调递减，
故得，即，
故选：D．
12． (2023·广东深圳·二模）已知，若过点可以作曲线的三条切线，则（ ）
A．B．C．D．
【答案】B
【解析】设切点为，切线方程为，由，所以，所以，
则，所以，
令，则，
因为，所以当或时，当时，
所以在和上单调递增，在上单调递减，
所以当时取得极大值，当时取得极小值，即，，
依题意有三个零点，所以且，即；故选：B
13． (2023·辽宁·辽师大附中）已知过点P(0，a)可作出曲线y=2x3–3x2的3条不同的切线，则实数a的取值范围是_______________ .
【答案】
【解析】函数,求导得,设切点为，
可得切线方程为，
又切线过点P(0，a)代入得，即
，由题意可得此方程有三个根，
令，，
当或时，，函数单调递增，
当时，，函数单调递减，
可得函数的极大值为，极小值为，若方程有三个根即函数的图象与x轴有三个交点，只需满足，即，故答案为：.
14． (2023·陕西·长安一中）已知函数，若过点存在三条直线与曲线相切，则的取值范围为___________．
【答案】
【解析】，
设过点的直线与曲线相切于点，
则，
化简得，，令，
则过点存在三条直线与曲线相切等价于y=g(x)与y=-m-2的图像有三个交点．
∵，
故当x<0或x>1时，，g(x)单调递增；当0又，，
∴g(x)如图，
∴-2<-m-2<0，即．故答案为：﹒
15． (2023·安徽蚌埠）已知函数，过点作曲线的切线，则可作切线的最多条数是______．
【答案】3
【解析】∵点不在函数的图象上，∴点不是切点，
设切点为（），
由，可得，
则切线的斜率，
∴，
解得或或，故切线有3条.故答案为：3.
题组五 公切线
1． (2023·海南）已知存在，使得函数与的图象存在相同的切线，且切线的斜率为1，则b的最大值为___.
【答案】-3
【解析】
令，得，切点为，
令，得，切点为.
切线方程为代入，可得则
令，则,当时，，当时，
∴h（x）在（0，1）上单调递增，在（1，+∞）上单调递减，
∴即b的最大值为-3.故答案为：-3.
2． (2023·安徽·安庆一中）若直线是曲线的切线，切点为，也是曲线的切线，切点为，则__________．
【答案】1
【解析】由直线是曲线的切线，切点为，
则直线的方程是，即
由直线是曲线的切线，
切点为，直线的方程为，即．
所以，所以，
因为，所以．故答案为：1
3． (2023·山东威海·三模）已知曲线，若有且只有一条直线同时与，都相切，则________．
【答案】1
【解析】设与相切于，与相切于点，由，得，则与相切于点的切线方程为：，即，
由，，则与相切于点的切线方程为：，即，，
因为两切线重合，所以，①，②，由①得
，代入②得，，化简得，
，明显可见，，时等式成立.故答案为：1
4． (2023·江西萍乡·三模（文））若存在实数，使得函数与的图象有相同的切线，且相同切线的斜率为，则实数的最大值为_________．
【答案】.
【解析】设函数的切点为，函数的切点为
分别对函数进行求导，，
由相同切线的斜率为，得
故切线方程为
故函数的切点为.
把切点代入中得
令，
当时，，函数单调递增
当时，，函数单调递减
故
故实数的最大值为
故答案为：.
5． (2023·山东师范大学附中模拟预测）已知函数，若存在一条直线同时与两个函数图象相切，则实数a的取值范围__________．
【答案】
【解析】数形结合可得：当，存在一条直线同时与两函数图象相切；
当，若存在一条直线同时与两函数图象相切，
则时，有解，
所以，
令，因为，
则当时，，为单调递增函数；
当时，，为单调递减函数；
所以在处取得极大值，也是最大值，
最大值为，且在上恒成立，
所以，即．
故答案为：
6． (2023·安徽·合肥市第八中学模拟预测（理））若曲线与曲线存在2条公共切线，则a的值是_________．
【答案】
【解析】设公切线在上的切点为，在上的切点为，
则曲线在切点的切线方程的斜率分别为，，
对应的切线方程分别为、，
即、，
所以，得，有，
则，整理，得，
设，则，，
令，令或，
所以函数在上单调递减，在和上单调递增，
因为两条曲线有2条公共切线，所以函数与图像有两个交点，
又，且，如图，
所以，解得.
故答案为：.
题组六 切线与其他知识的运用
1． (2023·湖南·株洲二中）已知，，直线与曲线相切，则的最小值是（ ）
A．B．C．D．
【答案】B
【解析】设直线与曲线相切于点，
，切线斜率，，即，
，；
，，
（当且仅当，即时取等号），
则的最小值为.故选：B.
2． (2023·江苏·苏州市苏州高新区第一中学）直线 分别与曲线， 直线 交于 两点， 则 的最小值为（ ）
A．B．C．D．
【答案】C
【解析】由题，设到直线的距离为，直线的倾斜角为，则 ，
又，，故最小即最小，即为当过点处的切线与直线平行时最小，
由曲线，得，所以切点为，
可求得点到直线的距离最小值为
故，
故选：C
3． (2023·广西·高三阶段练习）在平面直角坐标系中，是直线与曲线在第一象限的交点，是直线上的一点，且满足.为曲线上动点，当取最小值时，的横坐标为（ ）
A．B．C．D．
【答案】B
【解析】设，则.
又，设，，
则在直线上.又，故当直线与曲线相切时，最小.
此时，解得.
故选：B.
4． (2023·重庆市第十一中学校）二次函数的图象在点处的切线与轴交点的横坐标为，为正整数，，若数列的前项和为，则（ ）
A．B．C．D．
【答案】C
【解析】，在点处的切线斜率，
在点处的切线方程为：，即，
令，解得：，即，
数列是以为首项，为公比的等比数列，.
故选：C.
5． (2023·四川·石室中学二模（理））已知函数在x=0处的切线与直线平行，则二项式展开式中含项的系数为（ ）
A．26B．46C．36D．56
【答案】C
【解析】由函数的解析式，得，则．由题意，得，
则二项式，
二项式的通项公式为：，
所以含项的系数为．
故选：C
6． (2023·云南保山）已知曲线在点处的切线为l，数列的首项为1，点为切线l上一点，则数列中的最小项为（ ）
A．B．C．D．
【答案】C
【解析】因为，所以，
所以曲线在点处的切线的斜率.
所以切线l的方程为.所以.
所以数列是首项为1，公比为3的等比数列.所以.所以由，解得.
因为，所以.所以数列中的最小项为.故选：C.
7． (2023·湖南·模拟预测）已知抛物线，P为直线上一点，过P作抛物线的两条切线，切点分别为A，B，则的最小值为（ ）
A．B．-1C．D．-2
【答案】A
【解析】设，.由求导得，
则直线，直线，
联立方程可得，
由P在直线上，得，且，即.
因而
.
故选：A.
8． (2023·湖北·襄阳五中二模）已知函数在x=0处的切线与直线平行，则二项式展开式中含项的系数为_________．
【答案】36
【解析】由函数的解析式，得，则．由题意，得，
则二项式
展开式的通项为：
所以含项的系数为
故答案为：36．
题组七 切线方程的运用
1． (2023·广西·柳州市第三中学）曲线上的点到直线的距离的最小值为（ ）
A．B．
C．D．
【答案】D
【解析】，令得：，又，
故曲线上点到直线的距离最小值，所以最小值为.故选：D
2． (2023·江苏省太湖高级中学）若点P是曲线上任一点，则点P到直线的最小距离是（ ）
A．B．C．D．
【答案】C
【解析】解：设与直线平行的直线与曲线切于，
由定义域为，得，则，
由，解得（舍去负值）．
，则点到直线的最小距离是．故选：C．
3． (2023·山东·德州市教育科学研究院）已知函数，，若有两个零点，则k的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】令，则与有两个交点，则
设直线与相切时，切点坐标为，则斜率
则切线方程为
∵切线过原点，代入得，解得
∴，因为与有两个交点，所以
故选：D．
4． (2023·辽宁·沈阳二十中）若x、a、b为任意实数，若，则最小值为( )
A．B．9C．D．
【答案】C
【解析】由可得在以为圆心，1为半径的圆上，
表示点与点的距离的平方，
即表示圆上动点到函数y＝lnx图像上动点距离的平方．
设为y＝lnx上一点，且在处的y＝lnx的切线与和连线垂直，可得，即有，
由在时递增，且，可得m＝1，即切点为，
圆心与切点的距离为，
由此可得的最小值为．
故选：C．
5 (2023·河北保定）若函数有两个极值点，则实数a的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】，因为有两个极值点，故有两个根，
即和的图像有两个交点，画出图像，
若，显然1个交点，不合题意；若，设直线和相切于点，
则，解得，故切点是，故，解得.
故选：C.
6． (2023·山西·灵丘县第一中学校）已知函数若直线与有三个不同的交点，则实数的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】设与相切于点，
则，解得，此时，
由得，由可得，此时切点为，
作出函数与的图象如图，
由图象可知，当或时，直线与有三个不同的交点，故选：C
7． (2023·全国·高三专题练习（理））若点与曲线上点距离最小值为，则实数为_______.
【答案】
【解析】设点的坐标为，对函数求导得，
由题意可知，直线与曲线在点处的切线垂直，则，
得，
由两点间的距离公式得，
由于的最小值为，即，，解得，
因此，.
故答案为：
8． (2023·河北邯郸·二模）已知点P为曲线上的动点，O为坐标原点．当最小时，直线OP恰好与曲线相切，则实数a＝___．
【答案】
【解析】设，所以，
设，，
当时，，，所以单调递增，
当时，，，
所以单调递减，
当时，函数有最小值，即有最小值，所以，
此时直线OP的方程为，设直线与曲线相切于点，
由，显然在直线上，
则，因此有，
故答案为：
9． (2023·全国·高三专题练习）已知实数、、、满足，则的最小值为______．
【答案】
【解析】因为实数、、、满足，所以，，，
所以，点在曲线上，点在曲线上，
的几何意义就是曲线到曲线上点的距离最小值的平方．
考查曲线上和直线平行的切线，
对函数求导得，
令，解得，所以，切点为，
该切点到直线的距离就是所要求的两曲线间的最小距离，
故的最小值为．
故答案为：.