
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.2 三角公式的运用(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.3 三角函数的性质(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.4 正、余弦定理(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.1 等差数列(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.1 等差数列(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
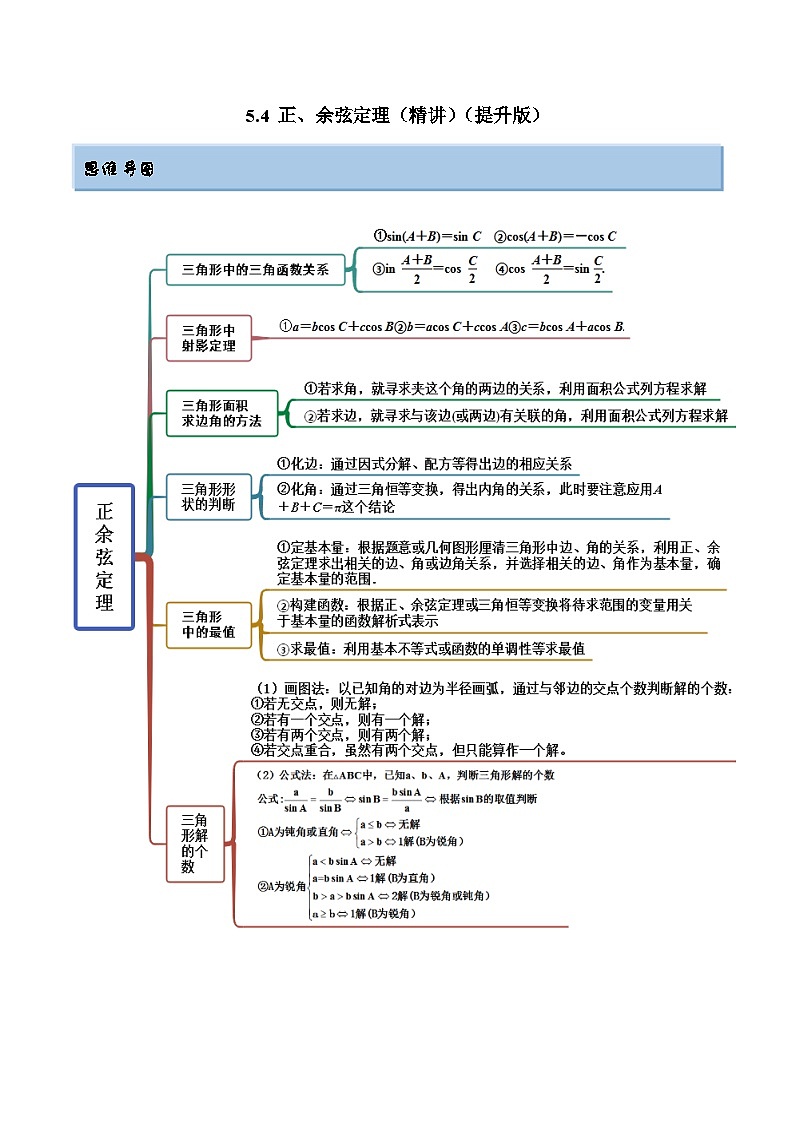
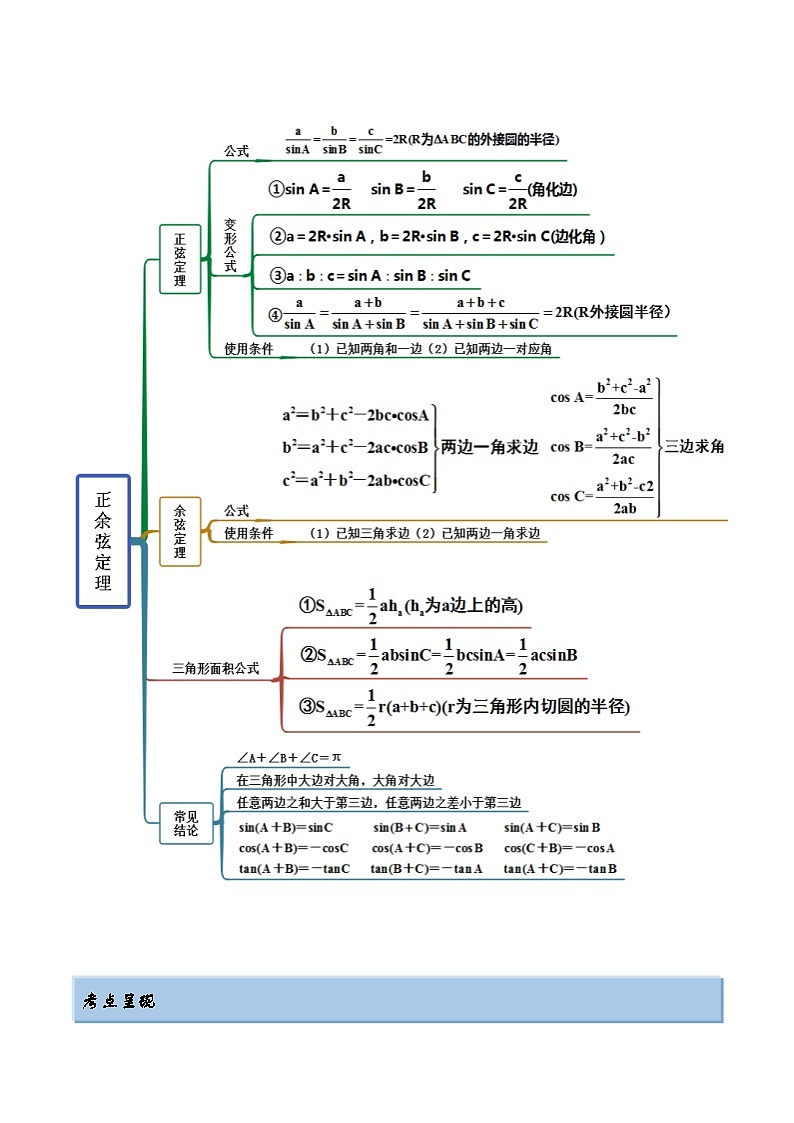
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.4 正、余弦定理(精讲)(提升版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 判断三角形的形状
【例1】 (2023·全国·高三专题练习)(多选)已知,,分别是三个内角,,的对边,下列四个命题中正确的是( )
A.若,则是锐角三角形
B.若,则是等腰三角形
C.若,则是等腰三角形
D.若,则是等边三角形
【一隅三反】
1. (2023·全国·高三专题练习)在△ABC中,内角A,B,C的对边分别为a,b,c已知,则△ABC的形状为( )
A.直角三角形B.等边三角形
C.等腰三角形D.等腰直角三角形
2. (2023·全国·高三专题练习)设△的三边长为,,,若,,则△是( ).
A.等腰三角形B.直角三角形
C.等腰三角形或直角三角形D.等腰直角三角形
3. (2023·全国·高三专题练习)已知的三条边和与之对应的三个角满足等式则此三角形的形状是( )
A.等腰三角形B.直角三角形
C.等腰或直角三角形D.等腰直角三角形
4. (2023·全国·高三专题练习)(多选)设的三个内角,,所对的边分别为,,.下列有关等边三角形的四个命题中正确的是( ).
A.若,则是等边三角形
B.若,则是等边三角形
C.若,则是等边三角形
D.若,则是等边三角形
考点二 最值问题
【例2-1】 (2023·河南·汝州市第一高级中学模拟预测(理))在中,角所对的边分别为,,,则面积的最大值是( )
A.B.C.D.
【例2-2】 (2023·江西·上饶市第一中学二模(文))在中,角A,B,C所对的边分别为a,b,c,,若点D在边上,且,则的最大值是___________.
【例2-3】 (2023·黑龙江·哈尔滨三中二模)在锐角中,角A,B,C的对边分别为a,b,c,的面积为S,若,则的取值范围为( )
A.B.C.D.
【一隅三反】
1. (2023·安徽黄山·二模(理))设的内角的对边分别为,且满足,其中,若,则面积的取值范围为______________.
3. (2023·全国·高三专题练习)已知锐角外接圆的半径为,内角,,所对边分别为,,,,则的取值范围是____.
4. (2023·甘肃·二模(理))如图,在圆内接四边形ABCD中,,且依次成等差数列.
(1)求边AC的长;
(2)求四边形ABCD周长的最大值.
5. (2023·广东江门·模拟预测)在锐角中,内角A,B,C的对边分别是a,b,c,且满足.
(1)求角B的大小;
(2)若,求的取值范围.
考点三 三角形解的个数
【例3-1】 (2023·全国·高三专题练习)在中,,,,则此三角形( )
A.无解B.一解
C.两解D.解的个数不确定
【例3-2】 (2023·全国·高三专题练习)在中,内角,,所对的边分别为,,,若,,当有两解时,的取值范围是( )
A.B.C.D.
【例3-3】 (2023·浙江·高三专题练习)中,角,,的对边分别是,,,,,若这个三角形有两解,则的取值范围是( )
A.B.
C.D.
【一隅三反】
1. (2023·全国·高三专题练习)在中,角A,B,C的对边分别是a,b,c,已知,使得三角形有两解的条件是( )
A.B.C.D.
2. (2023·全国·高三专题练习)在中,角A,B,C的对边分别是a,b,c,若,满足条件,的三角形有两个,则的取值范围是 ( )
A.B.C.D.
3. (2023·全国·高三专题练习)在中,,则“”是“有两个解”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
4. (2023·全国·高三专题练习)在中,角所对的边分别为,下列条件使有两解的是( )
A. B.
C. D.
考点四 几何中的正余弦定理
【例4】 (2023·浙江宁波·二模)如图,在中,,,点是线段的三等分点(靠近点),若,则___________,的面积是___________.
【一隅三反】
1. (2023·山东烟台·一模)如图,四边形ABCD中,.
(1)若,求△ABC的面积;
(2)若,,,求∠ACB的值.
2. (2023·陕西渭南·二模)如图,在中,角,D为边AC上一点,且,,
求:
(1)的值;
(2)边的长.
3. (2023·广东深圳·一模)如图,在△ABC中,已知,,,BC,AC边上的两条中线AM,BN相交于点P.
(1)求的正弦值;
(2)求的余弦值.
考点五 正余弦定理与平面向量的综合运用
【例5】 (2023·江西上饶·二模(理))已知的外心为点O,M为边上的一点,且,则的面积的最大值等于( )
A.B.C.D.
【一隅三反】
(2023·全国·高三专题练习)已知中,角A,B,C的对边分别为a,b,c,AH为BC边上的高,以下结论:① ;② 为锐角三角形;③ ;
④ 其中正确的个数是( )
A.1B.2C.3D.4
2. (2023·全国·高三专题练习)在中,若,则是的形状为( )
A.等腰三角形B.等边三角形
C.直角三角形D.钝角三角形
3. (2023·广东佛山·二模)中,,O是外接圆圆心,是的最大值为( )
A.0B.1C.3D.5
4. (2023·江西上饶·二模(理))已知的外心为点O,M为边上的一点,且,则的面积的最大值等于( )
A.B.C.D.
考点六 正余弦定理与其他知识的综合运用
【例6-1】 (2023·内蒙古赤峰·模拟预测(理))已知双曲线的左、右焦点分别为,,过点的直线与双曲线的右支交于A,B两点.,,则双曲线C的离心率为( )
A.2B.C.D.
【例6-2】 (2023·辽宁·育明高中高三阶段练习)在中,内角,,所对的边分别为,,,且的面积为,且恒成立,则的最小值为________.
【一隅三反】
1. (2023·全国·模拟预测)已知,是双曲线(,)的左、右焦点,点M为双曲线的左支上一点,满足,且,则该双曲线的离心率( )
A.B.C.D.2
2. (2023·江西·模拟预测(理))在中,角所对的边分別为,满足,若函数的图象向左平移个单位长度后的图象于轴对称,则在的值域为( )
A.B.C.D.
3. (2023·全国·哈师大附中模拟预测(理))椭圆C:()的左焦点为点F,过原点O的直线与椭圆交于P,Q两点,若∠PFQ=120°,,,则椭圆C的离心率为________.
5.4 正、余弦定理(精讲)(提升版)
思维导图
考点呈现
例题剖析
考点一 判断三角形的形状
【例1】 (2023·全国·高三专题练习)(多选)已知,,分别是三个内角,,的对边,下列四个命题中正确的是( )
A.若,则是锐角三角形
B.若,则是等腰三角形
C.若,则是等腰三角形
D.若,则是等边三角形
【答案】ACD
【解析】对于A,因为,所以,
,
因为,,为的内角,所以,,都是锐角,所以是锐角三角形,故选项A正确;
对于B:由及正弦定理,可得,
即,所以或,所以或,
所以是等腰三角形或直角三角形,故选项B错;
对于C:由及正弦定理化边为角,
可知,即,
因为,为的内角,所以,所以是等腰三角形,故选项C正确;
对于D:由和正弦定理化边为角,易知,所以,因为,,为的内角,所以,所以是等边三角形,故选项D正确;故选:ACD.
【一隅三反】
1. (2023·全国·高三专题练习)在△ABC中,内角A,B,C的对边分别为a,b,c已知,则△ABC的形状为( )
A.直角三角形B.等边三角形
C.等腰三角形D.等腰直角三角形
【答案】A
【解析】∵,可得,∴,∴,
∵,∴,∴,∴为直角三角形,且,
故选:A.
2. (2023·全国·高三专题练习)设△的三边长为,,,若,,则△是( ).
A.等腰三角形B.直角三角形
C.等腰三角形或直角三角形D.等腰直角三角形
【答案】B
【解析】设,△的内切圆半径为r,如图所示,
法一:
∴①;②.
①÷②,得:,即.
于是,
,,
从而得或,
∴或.故△为等腰三角形或直角三角形,
(1)当时,内心I在等腰三角形的底边上的高上,
,从而得.
又,代入①式,得,即,
上式两边同时平方,得:,化简,即.即△直角三角形,
∴△为等腰直角三角形.
(2)当时,易得.
代入②式,得,此式恒成立,
综上,△为直角三角形.
法二:
利用,及正弦定理和题设条件,得①,②.
∴③;④.
由③和④得:,即,,
因为为三角形内角,
∴或,即或.
(1)若,代入③得:⑤
又,将其代入⑤,得:.
变形得,
即⑥,
由知A为锐角,从而知.
∴由⑥,得:,即,从而,.
因此,△为等腰直角三角形.
(2)若,即,此时③④恒成立,
综上,△为直角三角形.
故选:B
3. (2023·全国·高三专题练习)已知的三条边和与之对应的三个角满足等式则此三角形的形状是( )
A.等腰三角形B.直角三角形
C.等腰或直角三角形D.等腰直角三角形
【答案】A
【解析】,可得,
整理,得,所以,
所以,所以,
所以,所以,
所以,所以或或,故三角形为等腰三角形.故选:A
4. (2023·全国·高三专题练习)(多选)设的三个内角,,所对的边分别为,,.下列有关等边三角形的四个命题中正确的是( ).
A.若,则是等边三角形
B.若,则是等边三角形
C.若,则是等边三角形
D.若,则是等边三角形
【答案】BCD
【解析】A,若,
由正弦定理可知:任意都满足条件,因此不一定是等边三角形,不正确;
B,若,由正弦定理可得:,∴,
∵,∴,∴是等边三角形,正确.
C,若,由正弦定理可得:,∴,
∵,∴,∴是等边三角形,正确.
D,若,∴,时,是等边三角形;
时,研究函数的单调性,
,时,,
∴函数在上单调递减,因此不成立.
综上可得:是等边三角形,正确.故选:BCD.
考点二 最值问题
【例2-1】 (2023·河南·汝州市第一高级中学模拟预测(理))在中,角所对的边分别为,,,则面积的最大值是( )
A.B.C.D.
【答案】A
【解析】由得:,
即,由正弦定理得:;
由余弦定理得:,,
即,,,
,
,,
,
则当时,,.故选:A.
【例2-2】 (2023·江西·上饶市第一中学二模(文))在中,角A,B,C所对的边分别为a,b,c,,若点D在边上,且,则的最大值是___________.
【答案】
【解析】由,得,因为,,所以,
设外接圆的圆心为,半径为,
则由正弦定理得,
如图所示,取的中点,
在中,;
在中,
,当且仅当圆心在上时取等号,所以的最大值是,
故答案为:.
【例2-3】 (2023·黑龙江·哈尔滨三中二模)在锐角中,角A,B,C的对边分别为a,b,c,的面积为S,若,则的取值范围为( )
A.B.C.D.
【答案】C
【解析】在中,,
故题干条件可化为,由余弦定理得,
故,又由正弦定理化简得:
,
整理得,故或(舍去),得
为锐角三角形,故,解得,故
故选:C
【一隅三反】
1. (2023·安徽黄山·二模(理))设的内角的对边分别为,且满足,其中,若,则面积的取值范围为______________.
【答案】
【解析】
,
化简得:,
由正弦定理可得:,
, ,
即, , 或,
即或,又,,即,
,又,,当仅当时等号成立,
,即,.
故答案为:
2. (2023·全国·高三专题练习)在 ABC中,角A,B,C的对边分别为a,b,c,若3acs C+b=0,则tan B的最大值是________.
【答案】
【解析】在 ABC中,因为3acs C+b=0,所以C为钝角,
由正弦定理得3sin Acs C+sin(A+C)=0,3sin Acs C+sin Acs C+cs Asin C=0,
所以4sin Acs C=-cs A·sin C,即tan C=-4tan A.
因为tan A>0,所以tan B=-tan(A+C)=-===
≤=,当且仅当tan A=时取等号,故tan B的最大值是.故答案为:
3. (2023·全国·高三专题练习)已知锐角外接圆的半径为,内角,,所对边分别为,,,,则的取值范围是____.
【答案】
【解析】因为,所以,,所以
,
因为,,所以,所以,
故,即,所以的取值范围是.
故答案为:.
4. (2023·甘肃·二模(理))如图,在圆内接四边形ABCD中,,且依次成等差数列.
(1)求边AC的长;
(2)求四边形ABCD周长的最大值.
【答案】(1)(2)10
【解析】(1)因为依次成等差数列,
所以,又,所以,
又,则由余弦定理得:,
所以.
(2由圆内接四边形性质及,知,
在中,由余弦定理得,
又因为(当且仅当时“=”成立),
所以,即,则四边形ABCD周长最大值.
5. (2023·广东江门·模拟预测)在锐角中,内角A,B,C的对边分别是a,b,c,且满足.
(1)求角B的大小;
(2)若,求的取值范围.
【答案】(1)(2)
【解析】(1)因为,
所以由正弦定理可得,化简得,
所以由余弦定理得,
因为,所以
(2)因为,所以,由正弦定理得,,
所以,
因为为锐角三角形,所以,得,所以,
所以,所以,,所以,即的取值范围为
考点三 三角形解的个数
【例3-1】 (2023·全国·高三专题练习)在中,,,,则此三角形( )
A.无解B.一解
C.两解D.解的个数不确定
【答案】C
【解析】在中,,,,
由正弦定理得,而为锐角,且,则或,
所以有两解.故选:C
【例3-2】 (2023·全国·高三专题练习)在中,内角,,所对的边分别为,,,若,,当有两解时,的取值范围是( )
A.B.C.D.
【答案】A
【解析】,即, 则
由,解得,则
当有两解时,,则,所以,故选:.
【例3-3】 (2023·浙江·高三专题练习)中,角,,的对边分别是,,,,,若这个三角形有两解,则的取值范围是( )
A.B.
C.D.
【答案】B
【解析】因为这个三角形有两解,故满足,即,解得.故选:B
【一隅三反】
1. (2023·全国·高三专题练习)在中,角A,B,C的对边分别是a,b,c,已知,使得三角形有两解的条件是( )
A.B.C.D.
【答案】B
【解析】,,到的距离,当时,三角形无解,
当时,三角形有一解,当时,三角形有两解,当时,三角形有一解.故选:.
2. (2023·全国·高三专题练习)在中,角A,B,C的对边分别是a,b,c,若,满足条件,的三角形有两个,则的取值范围是 ( )
A.B.C.D.
【答案】C
【解析】因为,,由正弦定理可得,所以,
又满足题意的三角形有两个,所以只需,即,
解得.故选:C.
3. (2023·全国·高三专题练习)在中,,则“”是“有两个解”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【解析】,若有两个解,则,即,即,
“”是“有两个解”的必要不充分条件.故选:B.
4. (2023·全国·高三专题练习)在中,角所对的边分别为,下列条件使有两解的是( )
A. B.
C. D.
【答案】D
【解析】选项A. 由余弦定理可得
的三边分别为,所以满足条件的三角形只有一个.
选项B. ,则, 由正弦定理可得
所以,的三边为定值,三个角为定值,所以满足条件的三角形只有一个.
选项C. 由,则由正弦定理可得
所以, 由则,所以角为一确定的角,且,
则角角为一确定的角,从而边也为定值,所以满足条件的三角形只有一个.
选项D. 作,在的一条边上取,过点作垂直于的另一边,垂足为.
则,以点为圆心,4为半径画圆弧,
因为,所以圆弧与的另一边有两个交点
所以均满足条件,所以所以满足条件的三角形有两个.
故选:D
考点四 几何中的正余弦定理
【例4】 (2023·浙江宁波·二模)如图,在中,,,点是线段的三等分点(靠近点),若,则___________,的面积是___________.
【答案】
【解析】在中,因为,可得,由,且,
在中,由正弦定理,可得,
因为,所以为锐角,所以,
又由
,
所以,所以,
设,
因为且点是线段的三等分点,可得,
在中,由余弦定理可得,
即,解得,所以,所以,
所以的面积为.故答案为:;.
【一隅三反】
1. (2023·山东烟台·一模)如图,四边形ABCD中,.
(1)若,求△ABC的面积;
(2)若,,,求∠ACB的值.
【答案】(1)(2)∠ACB=
【解析】(1)在△ABC中,,
因为,所以..
(2)设,则,,.
在△ACD中,由,得.
在△ABC中,由,得.
联立上式,并由得,
整理得,所以,
因为,所以,
所以,解得,即∠ACB的值为.
2. (2023·陕西渭南·二模)如图,在中,角,D为边AC上一点,且,,
求:
(1)的值;
(2)边的长.
【答案】(1)(2)
【解析】(1)在中, 由余弦定理的推论得,
,,
,
(2),,
,,
在中, 由正弦定理得,
3. (2023·广东深圳·一模)如图,在△ABC中,已知,,,BC,AC边上的两条中线AM,BN相交于点P.
(1)求的正弦值;
(2)求的余弦值.
【答案】(1)(2)
【解析】(1)解:解法1、由余弦定理得,
即,所以,所以,
在中,由余弦定理,得,
在中,由余弦定理,得,
与互补,则,解得,
在中,由余弦定理,得,
因为,所以.
解法2、由题意可得,,
由AM为边BC上的中线,则,
两边同时平方得,,故,
因为M为BC边中点,则的面积为面积的,
所以,
即,
化简得,.
(2)解:方法1、在中,由余弦定理,得,
所以,
由AM,BN分别为边BC,AC上的中线可知P为重心,
可得,,
在中,由余弦定理,得,
又由,所以.
解法2:
因为BN为边AC上的中线,所以,
,
,即.
所以.
考点五 正余弦定理与平面向量的综合运用
【例5】 (2023·江西上饶·二模(理))已知的外心为点O,M为边上的一点,且,则的面积的最大值等于( )
A.B.C.D.
【答案】C
【解析】因为,所以,
所以
所以,当且仅当时,取等号;
所以,当且仅当时,取等号;故选:C
【一隅三反】
(2023·全国·高三专题练习)已知中,角A,B,C的对边分别为a,b,c,AH为BC边上的高,以下结论:① ;② 为锐角三角形;③ ;
④ 其中正确的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】由AH为BC边上的高,
∴,而,故,①正确;
知:向量的夹角为钝角,即为锐角,而无法判断是否为锐角三角形,②错误;
,③正确;
,④正确.故选:C
2. (2023·全国·高三专题练习)在中,若,则是的形状为( )
A.等腰三角形B.等边三角形
C.直角三角形D.钝角三角形
【答案】C
【解析】由,可得,
又由余弦定理,可得,
整理得,所以是直角三角形.故选:C.
3. (2023·广东佛山·二模)中,,O是外接圆圆心,是的最大值为( )
A.0B.1C.3D.5
【答案】C
【解析】过点O作,垂足分别为D,E,如图,因O是外接圆圆心,则D,E分别为AC,的中点,
在中,,则,即,
,同理,
因此,
,
由正弦定理得:,当且仅当时取“=”,
所以的最大值为3.故选:C
4. (2023·江西上饶·二模(理))已知的外心为点O,M为边上的一点,且,则的面积的最大值等于( )
A.B.C.D.
【答案】C
【解析】因为,所以,
所以
所以,当且仅当时,取等号;
所以,当且仅当时,取等号;故选:C
考点六 正余弦定理与其他知识的综合运用
【例6-1】 (2023·内蒙古赤峰·模拟预测(理))已知双曲线的左、右焦点分别为,,过点的直线与双曲线的右支交于A,B两点.,,则双曲线C的离心率为( )
A.2B.C.D.
【答案】C
【解析】依题意,设,,由双曲线的定义得,,
在中,,由余弦定理,
得,解得,即,
设双曲线的焦距为2c,在中利用余弦定理有,解得,
所以双曲线的离心率为.故选:C
【例6-2】 (2023·辽宁·育明高中高三阶段练习)在中,内角,,所对的边分别为,,,且的面积为,且恒成立,则的最小值为________.
【答案】
【解析】由得, 所以,
由余弦定理得,所以,
化简得,显然关于的方程有解,
所以,化简得,即.
因为恒成立,所以恒成立,
令,则,而函数在上单调递减,在上单调递增,
又,且所以.故的最小值为.
故答案为:.
【一隅三反】
1. (2023·全国·模拟预测)已知,是双曲线(,)的左、右焦点,点M为双曲线的左支上一点,满足,且,则该双曲线的离心率( )
A.B.C.D.2
【答案】D
【解析】∵,由双曲线的定义得,
所以采用余弦定理:,
即,即,解得(负值舍去),则该双曲线的离心率.
故选:D.
2. (2023·江西·模拟预测(理))在中,角所对的边分別为,满足,若函数的图象向左平移个单位长度后的图象于轴对称,则在的值域为( )
A.B.C.D.
【答案】B
【解析】因为,故可得,
即,
又,故,联立,
可得,解得(舍去)或,
又,则,
将向左平移个单位长度后得到,
又因为其为偶函数,故,故,又,
故当时,满足题意,则,,
当时,,故.
故选:B.
3. (2023·全国·哈师大附中模拟预测(理))椭圆C:()的左焦点为点F,过原点O的直线与椭圆交于P,Q两点,若∠PFQ=120°,,,则椭圆C的离心率为________.
【答案】
【解析】根据题意,取椭圆的右焦点为,连接,作图如下:
由椭圆的对称性可知,四边形的对角线互相平分,
故四边形为平行四边形,则;
设,由椭圆定义可知,
在△和△中由余弦定理可得:
,
,
又,上述两式相加可得:
,即;
在△中,由余弦定理可得:,
即,则,;
故可得,则,又,故椭圆离心率为.
故答案为:.
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.1 等差数列(精讲)(提升版)(原卷版+解析版): 这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.1 等差数列(精讲)(提升版)(原卷版+解析版),共21页。试卷主要包含了等差中项,等差数列的前n项和性质,等差数列的最值,等差数列的综合运用,等差数列的实际运用等内容,欢迎下载使用。
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.4 正、余弦定理(精练)(提升版)(原卷版+解析版): 这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.4 正、余弦定理(精练)(提升版)(原卷版+解析版),共51页。试卷主要包含了最值问题,几何中的正余弦定理,正余弦定理与其他知识综合运用等内容,欢迎下载使用。
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.1 切线方程(精讲)(提升版)(原卷版+解析版): 这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.1 切线方程(精讲)(提升版)(原卷版+解析版),共26页。试卷主要包含了斜率和倾斜角,“在型”的切线方程,“过型”的切线方程,切线或切点数量问题,公切线,切线方程的运用等内容,欢迎下载使用。












