2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.4 对数运算及对数函数（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.4 对数运算及对数函数（精讲）（提升版）（原卷版+解析版），共25页。试卷主要包含了对数运算，对数函数的单调性，对数函数的值域，对数式比较大小，解对数式不等式，对数函数的定点等内容，欢迎下载使用。
考点呈现
例题剖析
考点一 对数运算
【例1】 (2023·全国·高三专题练习）化简求值
（1）；
（2）；.
（3）；．
（4）.
【一隅三反】
(2023·全国·高三专题练习）化简求值：
（1）． （2）；
（3）. （4）
（5）．
考点二 对数函数的单调性
【例2-1】 (2023·全国·高三专题练习）若函数在区间内单调递增，则实数的取值范围为（ ）
A．B．C．D．
【例2-2】 (2023·天津·南开中学二模）已知函数是R上的单调函数，则实数a的取值范围为（ ）
A．B．
C．D．
【一隅三反】
1． (2023·全国·高三专题练习）函数的单调递增区间为____________．
2． (2023·全国·高三专题练习）已知函数f(x)＝lg(x2－2x－3)在(－∞，a)单调递减，则a的取值范围是（ ）
A．(－∞，－1]B．(－∞，2]C．[5，＋∞)D．[3，＋∞)
3． (2023·天津市武清区大良中学高三阶段练习）若函数在R上单调递增，则实数a的取值范围是_______
4．（2022·河北）已知函数在区间上是增函数，求实数的取值范围_____．
考点三 对数函数的值域（最值）
【例3-1】（2022·全国·高三专题练习）函数的最小值为（ ）
A．B．C．D．0
【例3-2】 (2023·四川·宜宾市教科所三模）若函数的值域为，则的取值范围是( )
A．B．C．D．
【例3-3】 (2023·重庆·模拟预测）若函数有最小值，则实数a的取值范围是（ ）
A．B．
C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知，，则的值域为（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）若函数且的值域为，则的取值范围为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）若函数的值域为，则实数的取值范围是（ ）
A．B．C．D．
4． (2023·全国·高三专题练习）已知函数的值域为R，则实数a的取值范围是（ ）
A．B．C．D．
考点四 对数式比较大小
【例4-1】 (2023·江苏常州·模拟预测）已知，则正确的大小顺序是（ ）
A．B．C．D．
【例4-2】 (2023·新疆乌鲁木齐·模拟预测（理））设，则（ ）
A．B．
C．D．
【一隅三反】
1． (2023·浙江·模拟预测）己知实数，且，则（ ）
A．B．C．D．
2． (2023·全国·模拟预测）定义在R上的函数满足，当时，，设，，，则a，b，c的大小关系是（ ）
A．B．C．D．
3． (2023·浙江金华·三模）若函数，设，，，则下列选项正确的是（ ）
A．B．
C．D．
4． (2023·广东佛山·三模）（多选）已知，则下列不等式成立的是（ ）
A．B．C．D．
考点五 解对数式不等式
【例5-1】 (2023·河南濮阳）已知函数是R上的偶函数，且在上恒有，则不等式的解集为（ ）
A．B．1,e2C．D．
【例5-2】 (2023·湖北·二模）已知函数，则使不等式成立的x的取值范围是（ ）
A．B．
C．D．
【一隅三反】
1． (2023·河南·高三阶段练习（理））设函数，则不等式的解集为（ ）
A．B．
C．D．
2． (2023·江西·奉新县第一中学高三阶段练习（理））已知函数，若，则实数a的取值范围是（ ）
A．B．C．D．
3． (2023·安徽·高三阶段练习（理））已知函数，则不等式的解集为（ ）
A．B．
C．D．
考点六 对数函数的定点
【例6】 (2023·四川·德阳五中）若函数的图象经过定点，且点在角的终边上，则（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知函数（且）的图象过定点，且角的终边经过，则（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）已知正数，，函数（且）的图象过定点，且点在直线上，则的最小值为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）已知数列为等比数列，函数过定点，，数列的前项和为，则（ ）
A．44B．45C．46D．50
3.4 对数运算及对数函数（精讲）（提升版）
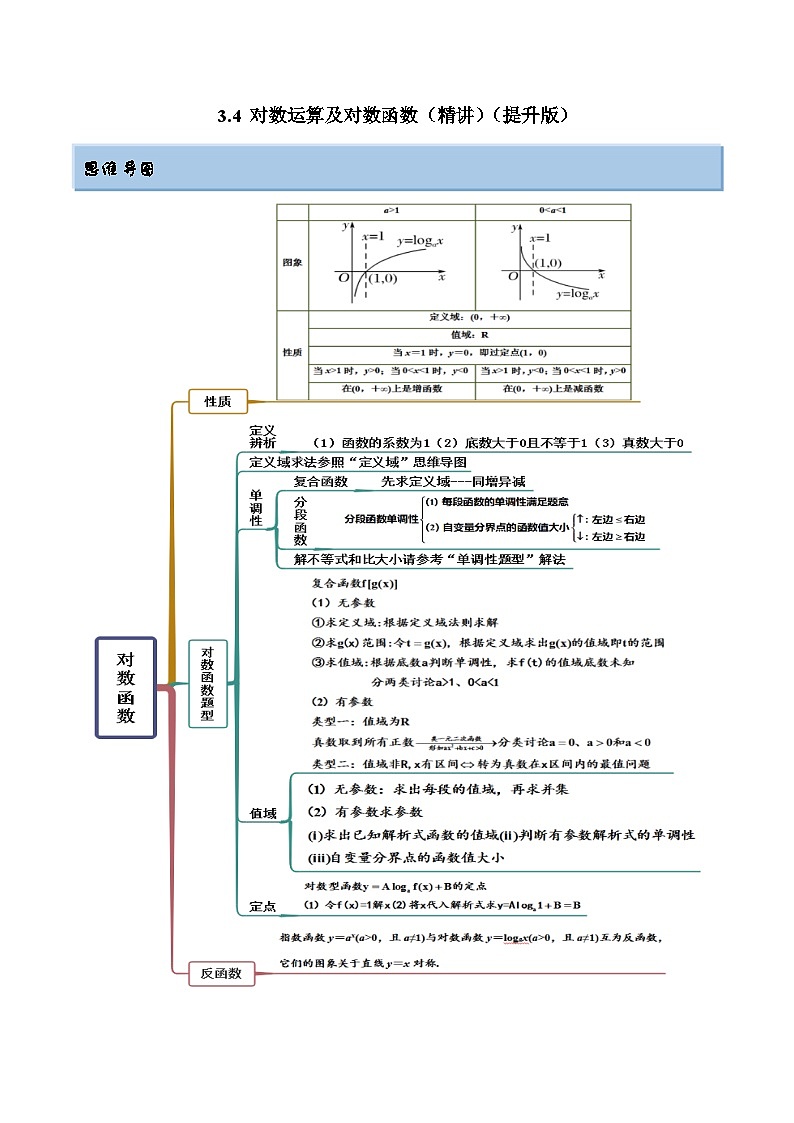
思维导图
考点呈现
例题剖析
考点一 对数运算
【例1】 (2023·全国·高三专题练习）化简求值
（1）；
（2）；.
（3）；．
（4）.
【答案】（1）1；（2）1；（3）4；（4）2.
【解析】（1）；
（2）；
（3）
；
（4）
【一隅三反】
(2023·全国·高三专题练习）化简求值：
（1）．
（2）；
（3）.
（4）
（5）．
【答案】（1）5；（2）3；（3）0；（4）3；（5）.
【解析】（1）

；
（2）
；
（3）
；
（4）
；
（5）
．
考点二 对数函数的单调性
【例2-1】 (2023·全国·高三专题练习）若函数在区间内单调递增，则实数的取值范围为（ ）
A．B．C．D．
【答案】C
【解析】，函数定义域满足：，解得，
在上单调递减，
根据复合函数单调性知，在单调递减，函数对称轴为，
故，解得.故选：C.
【例2-2】 (2023·天津·南开中学二模）已知函数是R上的单调函数，则实数a的取值范围为（ ）
A．B．
C．D．
【答案】B
【解析】当函数是R上的单调递减函数，所以，解得，
因为且，所以当时，不可能是增函数，所以函数在R上不可能是增函数，
综上：实数a的取值范围为，故选：B
【一隅三反】
1． (2023·全国·高三专题练习）函数的单调递增区间为____________．
【答案】
【解析】由得，所以函数的定义域为.
令，则，，开口向上，对称轴为，
所以在上递增，在定义域内单调递增，
所以)在上单调递增，所以函数的单调递增区间是.
故答案为：.
2． (2023·全国·高三专题练习）已知函数f(x)＝lg(x2－2x－3)在(－∞，a)单调递减，则a的取值范围是（ ）
A．(－∞，－1]B．(－∞，2]C．[5，＋∞)D．[3，＋∞)
【答案】A
【解析】是增函数，在上递减，在递增，
因此在上递减，则有，解得．故选：A．
3． (2023·天津市武清区大良中学高三阶段练习）若函数在R上单调递增，则实数a的取值范围是_______
【答案】
【解析】由，在R上单调递增，
∴在上递增，在上也递增，
由增函数图象特征知：不能在点上方，综上， ，解得，
∴实数a的取值范围是.故答案为：.
4．（2022·河北）已知函数在区间上是增函数，求实数的取值范围_____．
【答案】
【解析】令，因为外层函数为减函数，则内层函数在区间上是减函数，所以，，解得.故答案为：.
考点三 对数函数的值域（最值）
【例3-1】（2022·全国·高三专题练习）函数的最小值为（ ）
A．B．C．D．0
【答案】A
【解析】由题意知的定义域为.
所以，，
，时等号成立．故选：A.
【例3-2】 (2023·四川·宜宾市教科所三模）若函数的值域为，则的取值范围是( )
A．B．C．D．
【答案】C
【解析】当时，f(x)=，
当时，f(x)=，
故要使的值域是，则0≤≤1，解得．故选：C．
【例3-3】 (2023·重庆·模拟预测）若函数有最小值，则实数a的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】依题意且，所以，解得或，综上可得，
令的根为、且，，，
若，则在定义域上单调递增，在上单调递增，在上单调递减，
根据复合函数的单调性可知，在上单调递增，在上单调递减，函数不存在最小值，故舍去；
若，则在定义域上单调递减，在上单调递增，在上单调递减，
根据复合函数的单调性可知，在上单调递减，在上单调递增，所以函数在取得最小值，所以；故选：A
【一隅三反】
1． (2023·全国·高三专题练习）已知，，则的值域为（ ）
A．B．C．D．
【答案】B
【解析】因为，，所以的定义域为，
解得，所以该函数的定义域为；所以，
所以
，所以，
当时，，当时，，所以；所以函数的值域是．故选：B．
2． (2023·全国·高三专题练习）若函数且的值域为，则的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】当时，，，
当时，，
∵函数的值域为，∴，又，
∴，即，∴的取值范围为.故选：D．
3． (2023·全国·高三专题练习）若函数的值域为，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】由题可知，函数的值域包含，当时，符合题意；
当时，则，解得；
当时，显然不符合题意，故实数的取值范围是．
故选：A.
4． (2023·全国·高三专题练习）已知函数的值域为R，则实数a的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】∵，又函数的值域为R，
则，解得．故选：C．
考点四 对数式比较大小
【例4-1】 (2023·江苏常州·模拟预测）已知，则正确的大小顺序是（ ）
A．B．C．D．
【答案】B
【解析】因为，所以，
因为，所以，所以.故选：B.
【例4-2】 (2023·新疆乌鲁木齐·模拟预测（理））设，则（ ）
A．B．
C．D．
【答案】D
【解析】令，则，
因为函数在上递增，所以函数在上递增，
所以，所以函数在上递增，
所以，即，即，
令，令，令，
则，所以函数在上递增，所以，
所以，故，即，所以，综上所述，.
故选：D.
【一隅三反】
1． (2023·浙江·模拟预测）己知实数，且，则（ ）
A．B．C．D．
【答案】A
【解析】由可得，
因为在上单调递增，且，，所以，即，
其次，，所以，
又因为且单调递增，所以由可知，综上，．
故选：A
2． (2023·全国·模拟预测）定义在R上的函数满足，当时，，设，，，则a，b，c的大小关系是（ ）
A．B．C．D．
【答案】D
【解析】由知： 关于直线x=1对称.
当时，，
由复合函数的单调性知：在上单调递增.
又，
而，，，
所以.故选：D.
3． (2023·浙江金华·三模）若函数，设，，，则下列选项正确的是（ ）
A．B．
C．D．
【答案】A
【解析】由题可知，故，∴函数为偶函数；
易知，当时，在为单调递增函数；又，∴，
同理，；又，
，故，故.
故选：A.
4． (2023·广东佛山·三模）（多选）已知，则下列不等式成立的是（ ）
A．B．C．D．
【答案】BC
【解析】选项A：
由，可得，
则，，
则，则.判断错误；
选项B：由，可得为上减函数，
又，则.判断正确；
选项C：由，可知为R上减函数，又，则
由，可知为上增函数，又，则，则
又为上增函数，则，则.判断正确；
选项D：令，则，
，
则，即.判断错误.故选：BC
考点五 解对数式不等式
【例5-1】 (2023·河南濮阳）已知函数是R上的偶函数，且在上恒有，则不等式的解集为（ ）
A．B．1,e2C．D．
【答案】C
【解析】因为函数是R上的偶函数，所以关于直线对称，在上恒有，当时，，所以在单调递减，在单调递增，不等式需满足，解得.故选：C．
【例5-2】 (2023·湖北·二模）已知函数，则使不等式成立的x的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】由得定义域为，
，故为偶函数，
而，在上单调递增，故在上单调递增，
则可化为，得解得故选：D
【一隅三反】
1． (2023·河南·高三阶段练习（理））设函数，则不等式的解集为（ ）
A．B．
C．D．
【答案】A
【解析】依题意，当时，由得：，解得，则，
当时，由得： ，即0