数学八年级下册18.1.2 平行四边形的判定课文内容ppt课件

这是一份数学八年级下册18.1.2 平行四边形的判定课文内容ppt课件，共22页。PPT课件主要包含了端点不同，两条线段的关系，位置关系，数量关系，DE与BC的关系，DE∥BC，问题4，三角形中位线定理，符号语言，DEDF等内容，欢迎下载使用。

学习目标1. 理解三角形中位线的概念，掌握三角形中位线定理. 2. 通过探索，猜想，证明三角形的中位线定理，进一步发展推理论证的能力.
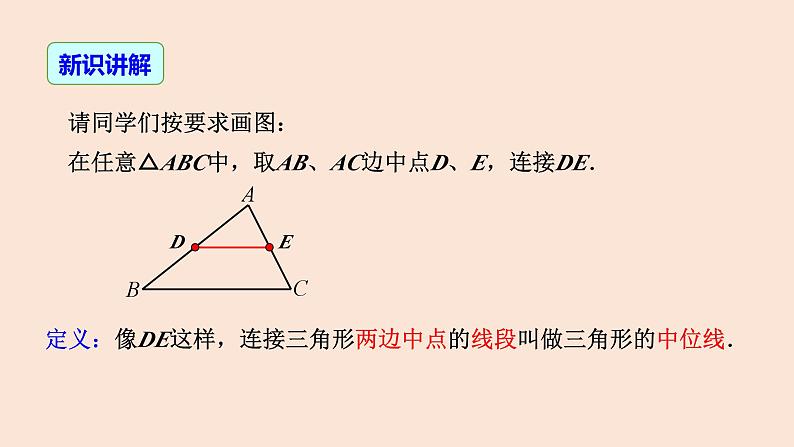
请同学们按要求画图：在任意△ABC中，取AB、AC边中点D、E，连接DE．
定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线．
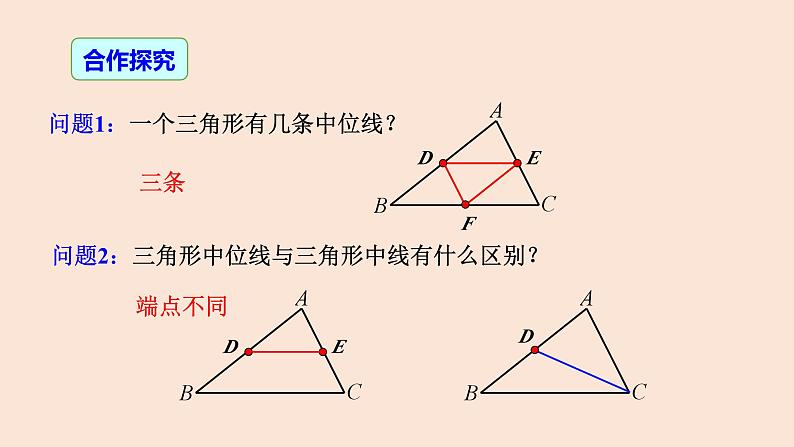
问题1：一个三角形有几条中位线？
问题2：三角形中位线与三角形中线有什么区别？
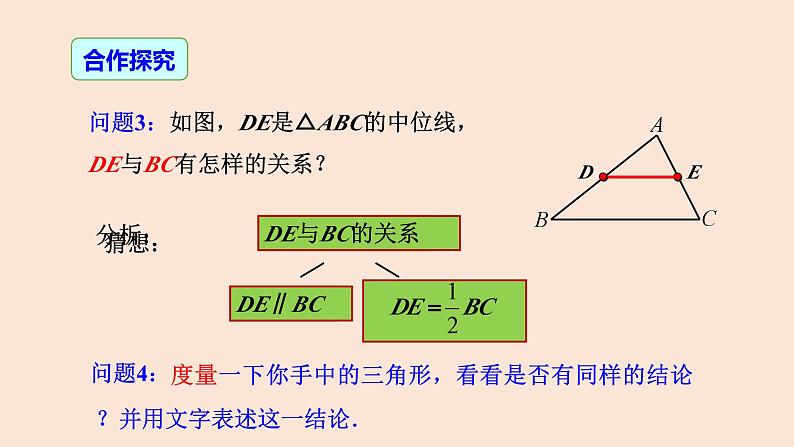
问题3：如图，DE是△ABC的中位线，DE与BC有怎样的关系？
度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论．
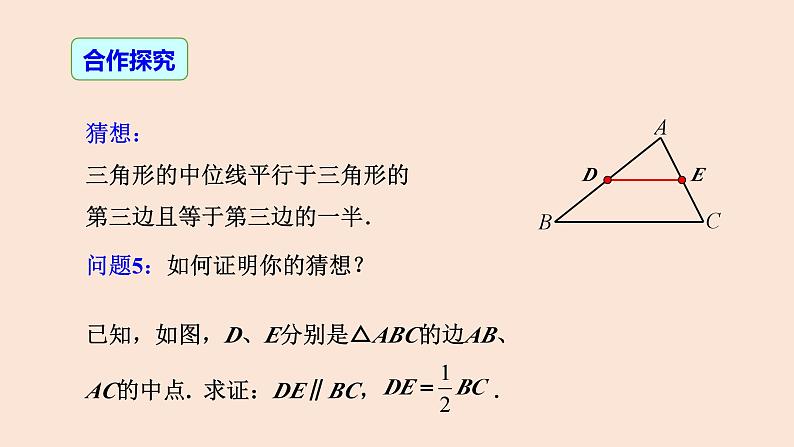
猜想：三角形的中位线平行于三角形的第三边且等于第三边的一半．
问题5：如何证明你的猜想？
延长DE到F，使EF=DE．
连接AF、CF、DC ．
∵AE=EC，DE=EF ，
∴四边形ADCF是平行四边形．
∴四边形BCFD是平行四边形．
∴ DE∥BC， ．
三角形的中位线平行于三角形的第三边且等于第三边的一半．
例：在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点. 求证：四边形EFGH是平行四边形.
1. 如图，△ABC中，D、E分别是AB、AC的中点，BC=10cm，则DE=______.
2. 如图， △ABC中，D、E分别是AB、AC的中点，∠A=50°，∠B=70°，则∠AED=_____.
3. 如图，在△ABC中，∠C=90°，AC=8，CB=6，D，E，F分别是BC，AC，AB的中点，则四边形AEDF的周长为________；Rt△ABC的中位线分别是___________；斜边上的中线是_______，其长为______.
4. 在△ABC中，D、E、F分别是AB、BC、CA的中点.以这些点为顶点，在图中，你能画出多少个平行四边形？为什么？
解：3个.平行四边形DFCE,平行四边形DFEB,平行四边形DEFA.
5. 已知：如图所示，在△ABC中，点D是AB的中点，点E是AC的中点，点F是BC的中点，连接DE，AF.求证：线段DE、AF互相平分．
证明：连接DF、EF，∵点D是AB的中点，点E是AC的中点，点F是BC的中点，∴DF∥AE，EF∥AD，∴四边形ADFE是平行四边形，∴ DE、AF互相平分．
6. 如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样量出A、B两点间的距离？根据是什么？
解：分别找出AC、BC中点M、N，量出M、N两点间距离，则AB=2MN.
根据是三角形中位线定理．
如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA中点．求证：四边形EFGH是平行四边形．
1.（2分）（2021•青海17/25）如图，在△ABC中，D，E，F分别是边AB，BC，CA的中点，若△DEF的周长为10，则△ABC的周长为 ．
【分析】先根据三角形中位线的性质得：AB＝2EF，BC＝2DF，AC＝2DE，根据周长得：EF+DE+DF＝10，所以2EF+2DE+2DF＝20，即AB+BC+AC＝20．
2.（4分）（2021•重庆B卷17/26）如图，△ABC中，点D为边BC的中点，连接AD，将△ADC沿直线AD翻折至△ABC所在平面内，得△ADC＇，连接CC＇，分别与边AB交于点E，与AD交于点O．若AE=BE，BC＇=2，则AD的长为　3　．
1. 三角形中位线的定义:____________________________ 叫做三角形的中位线 .2. 三角形的中位线与中线的区别：中位线是_____________的连线；中线是_____________的连线.3. 三角形的中位线定理：三角形的中位线______于三角形的第三边，并且等于第三边的______．
连接三角形两边中点的线段