华师大版八年级数学下册 第18章 平行四边形 第4课时 多个平行四边形结合的综合运用（课件）

这是一份华师大版八年级数学下册 第18章 平行四边形 第4课时 多个平行四边形结合的综合运用（课件），共17页。

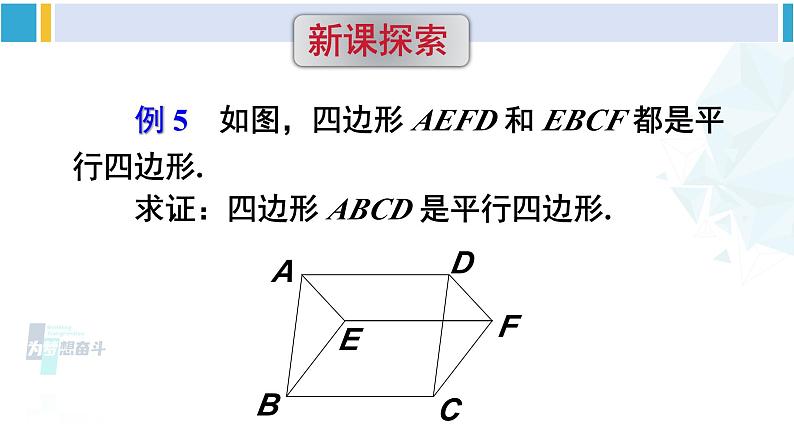
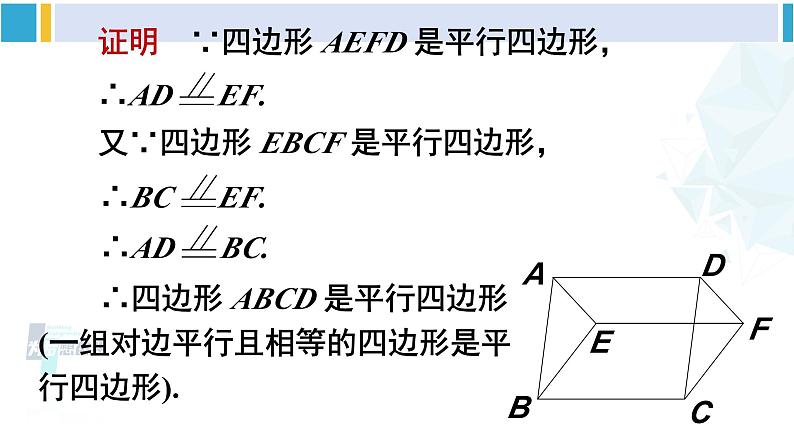
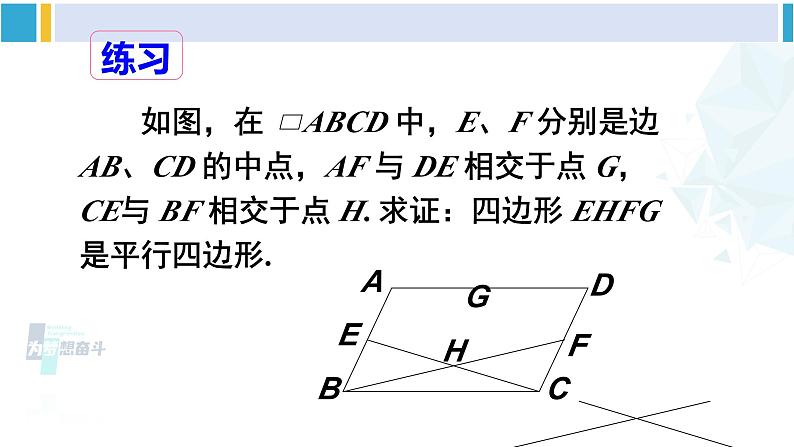
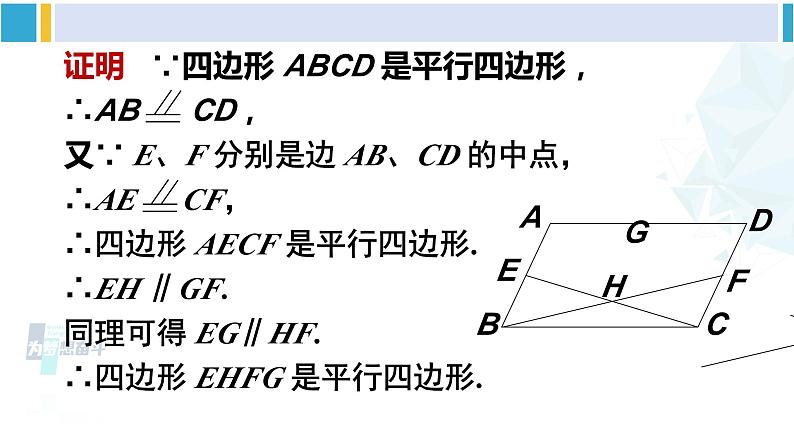
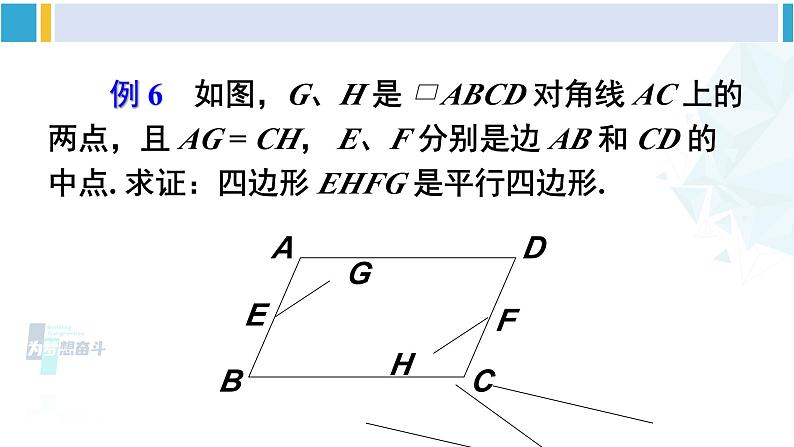
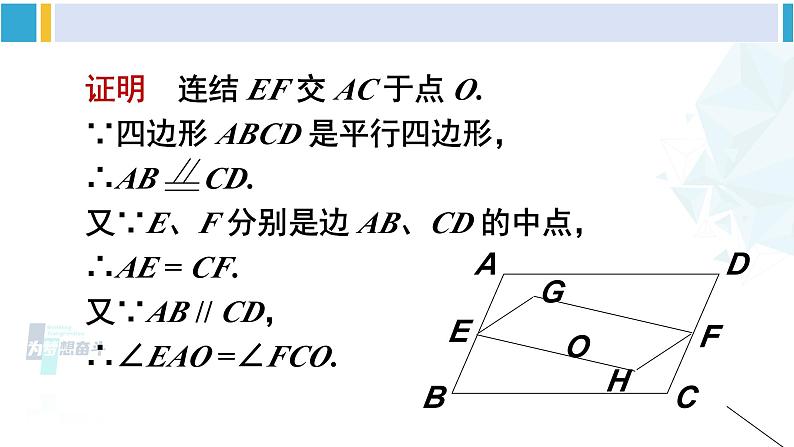
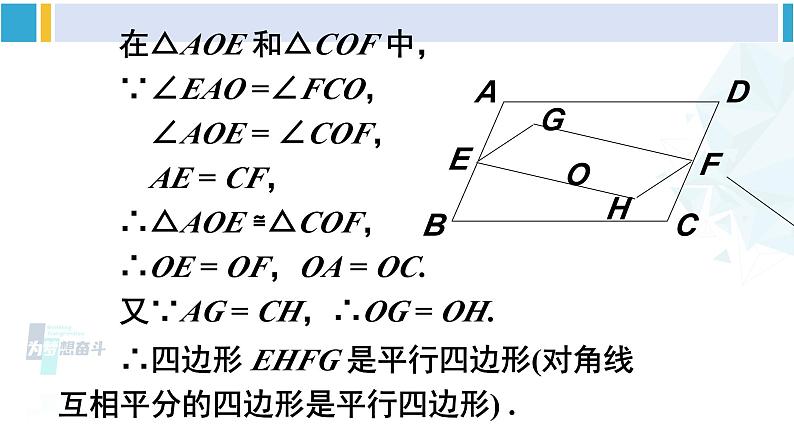
第4课时 多个平行四边形结合的综合运用华东师大版八年级数学下册 例 5 如图，四边形 AEFD 和 EBCF 都是平行四边形. 求证：四边形 ABCD 是平行四边形. 如图，在 ABCD 中，E、F 分别是边AB、CD 的中点，AF 与 DE 相交于点 G，CE与 BF 相交于点 H. 求证：四边形 EHFG是平行四边形. 例 6 如图，G、H 是 ABCD 对角线 AC 上的两点，且 AG = CH， E、F 分别是边 AB 和 CD 的中点. 求证：四边形 EHFG 是平行四边形.在△AOE 和△COF 中，∵∠EAO =∠FCO， ∠AOE = ∠COF， AE = CF，∴△AOE ≌△COF，∴OE = OF，OA = OC.又∵AG = CH，∴OG = OH. ∴四边形 EHFG 是平行四边形(对角线互相平分的四边形是平行四边形) . 如图，在四边形 ABCD 中，M 是边 BC 的中点，AM、BD 互相平分并交于点 O. 求证: AM DC. 1. 如图所示， ABCD 中，AC 的垂直平分线交 AD 于点 E，且△CDE 的周长为 8，则 ABCD 的周长是（ ） A. 10 B. 12 C. 14 D. 16D 2. 如图，已知平行四边形 ABCD 中，△DEC 和△FBC 都是等边三角形，则∠AEF =________.60° 3. 如图，在 ABCD 的形外分别作等腰直角三角形 ABF 和等腰直角三角形 ADE，∠ FAB =∠EAD = 90°，连结 AC，EF. 在图中找一个与△FAE 全等的三角形，并加以证明.解 △FAE≌△ABC证明∵四边形 ABCD 是平行四边形∴AD = BC，AD// BC,∴∠BAD +∠ABC = 180°.∵△ABF 和△ADE 是等腰直角三角形，∴AF = AB，AE = AD，∠BAF =∠ DAE = 90°，∴AE = BC. ∵ ∠FAE +∠BAD = 180°，∴∠FAE = ∠ABC.∴△FAE≌△ABC. 4. 如图，C 是 AB 的中点，AD = CE，CD = BE. 求证：四边形 CBED 是平行四边形. 证明 在△ACD 与△CBE 中， AD = CE，CD = BE，AC = CB， ∴△ACD ≌△CBE. ∴∠ACD =∠B，CD // BE. 又∵CD = BE， ∴四边形 CBED 是平行四边形（一组对边平行且相等的四边形是平行四边形）1.从教材习题中选取，2.完成练习册本课时的习题.