华师大版八下数学 18.4平行四边形 小结 教案

第18章平行四边形复习

教学目标：

1.熟悉平行四边形的定义、性质、判定、对称性

2.通过例题和练习，提高学生综合分析问题、解决问题的能力和应变能力；

重点难点：

1、重点：平行四边形的概念和特征。

2、难点：灵活运用平行四边形的概念和特征解决实际问题

复习过程：

考点１：平行四边形的定义：       

1.两组对边分别平行的四边形叫做平行四边形。

2.平行四边形是中心对称图形,对称中心是两条对角线的交点.

考点２：平行四边形的性质：       

边：对边平行且相等；

角：对角相等，邻角互补；

对角线：互相平分；

两条平行线间的距离:两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.平行线之间的距离处处相等.【

考点3：平行四边形的判定：

两组对边分别平行；

    两组对边分别相等；

一组对边平行且相等；

对角线互相平分；

考点4：对称性

中心对称图形 

合作探究：

一、平行四边形：探究引路

1、①如图,在四边形ABCD中,AD∥BC、AB∥CD,过点P画线段EF、GH分别平行于AB、BC,则图中共有平行四边形(    )个

A、7        B、8        C、9        D、10

平行四边形：应用迁移

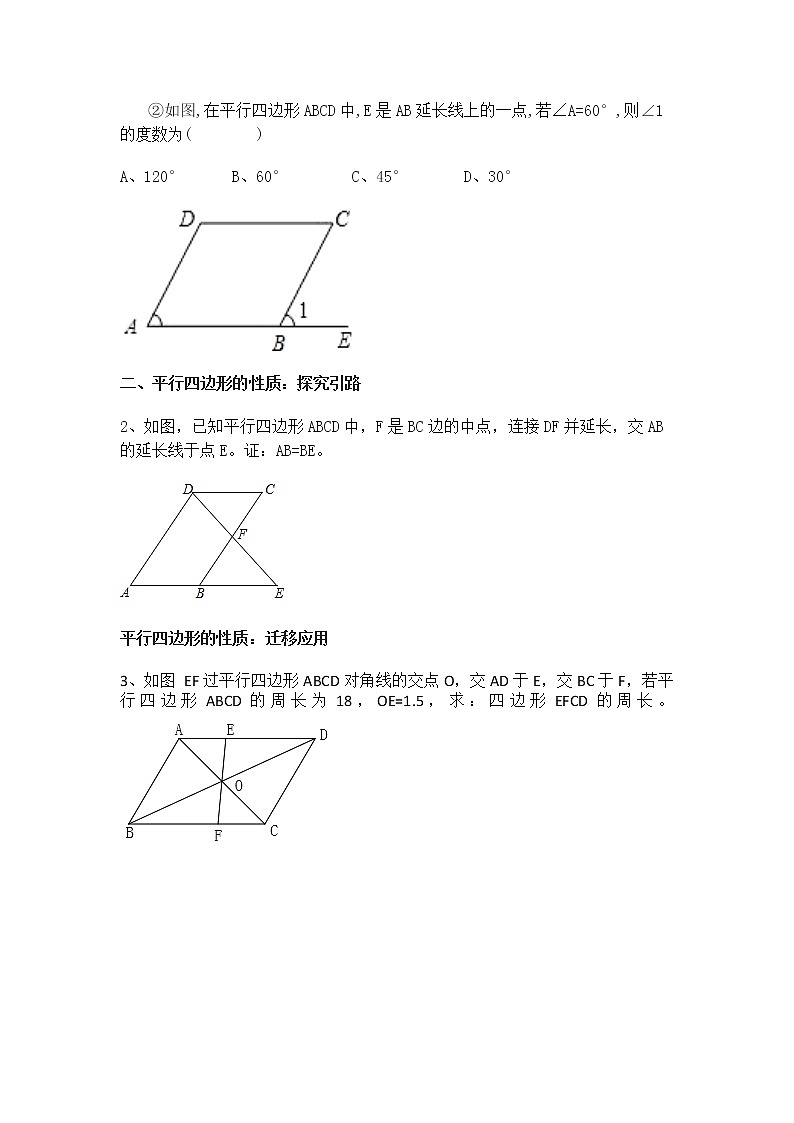
②如图,在平行四边形ABCD中,E是AB延长线上的一点,若∠A=60°,则∠1的度数为(    )

A、120°      B、60°        C、45°       D、30°

二、平行四边形的性质：探究引路

2、如图，已知平行四边形ABCD中，F是BC边的中点，连接DF并延长，交AB的延长线于点E。证：AB=BE。

平行四边形的性质：迁移应用

3、如图 EF过平行四边形ABCD对角线的交点O，交AD于E，交BC于F，若平行四边形ABCD的周长为18，OE=1.5，求：四边形EFCD的周长。

平行四边形的性质：中考考点链接

4、已知□ABCD的对角线AC，BD交于点O,且AC=8，BD=10，AB=5，则△OCD的周长为         

三、平行四边形的判定：探究引路

5、如图,分别以△ABC的三边为边长,在BC的同侧作

等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.

四、课后作业

6、如图， E、F是四边形ABCD的对角线BD上的两点，

BF=DE，AE=CF，∠1=∠2。

（1）求证：三角形ABE≌△CDF。

（2）四边形ABCD是平行四边形吗？请说明理由。

7、如图，平行四边形ABCD中，E、F分别是边BC、AD的中点，求证：∠ABF=∠CDE．

8、如图，在△ABC中，∠ACB=90°，∠CAB=30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F．

求证：四边形BCFD为平行四边形；