

2023年华东师大版数学八年级下册《平行四边形》单元质量检测(含答案)
展开2023年华东师大版数学八年级下册
《平行四边形》单元质量检测
一 、选择题
1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )
A.30° B.45° C.60° D.75°
2.如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )
A.155° B.130° C.125° D.110°
3.如图,在▱ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( )
A.12 B.15 C.18 D.21
4.已知O为平行四边形ABCD对角线的交点,△AOB的面积为1,则平行四边形的面积为( )
A.1 B.2 C.3 D.4
5.下列条件不能判断四边形是平行四边形的是( )
A.两组对边分别相等
B.一组对边平行且相等
C.一组对边平行,另一组对边相等
D.对角线互相平分
6.下列说法正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是平行四边形
D.对角线互相垂直且相等的四边形是平行四边形
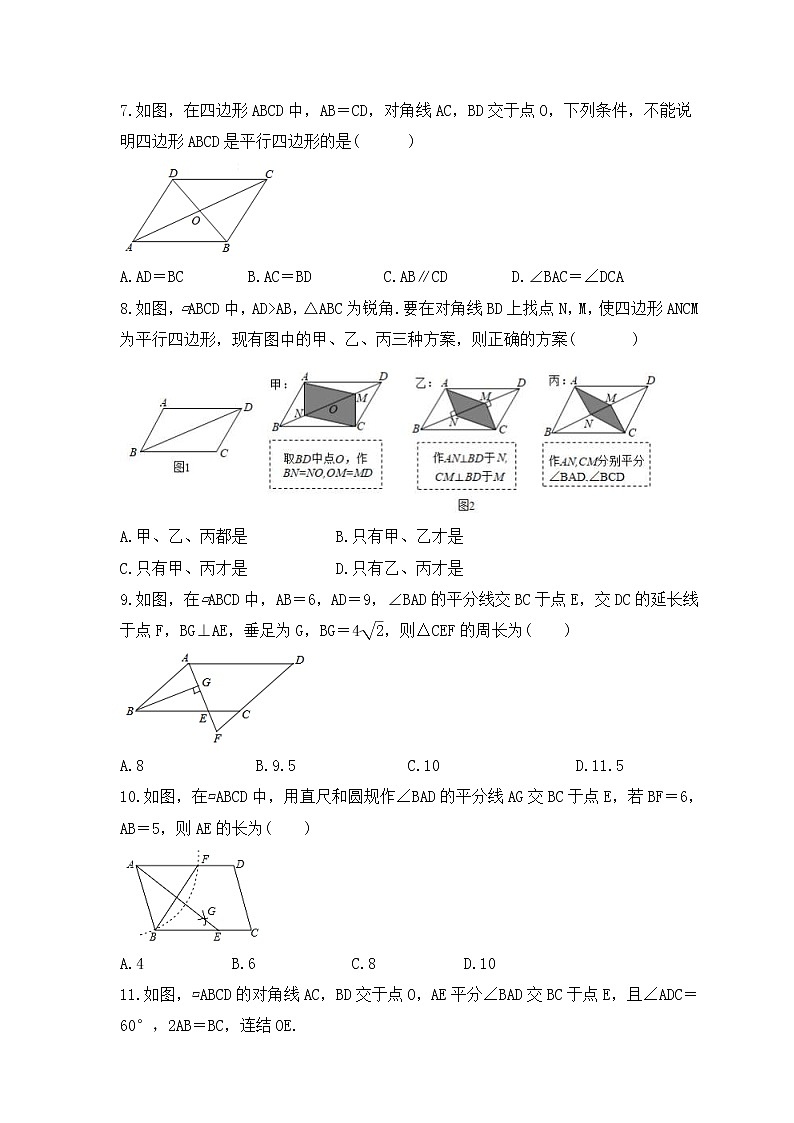
7.如图,在四边形ABCD中,AB=CD,对角线AC,BD交于点O,下列条件,不能说明四边形ABCD是平行四边形的是( )
A.AD=BC B.AC=BD C.AB∥CD D.∠BAC=∠DCA
8.如图,▱ABCD中,AD>AB,△ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图中的甲、乙、丙三种方案,则正确的方案( )
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
9.如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4,则△CEF的周长为( )
A.8 B.9.5 C.10 D.11.5
10.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.6 C.8 D.10
11.如图,▱ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,2AB=BC,连结OE.
下列结论:①∠CAD=30°;②S▱ABCD=AB·AC;③OB=AB;④4OE=BC.
成立的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
①2∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
A.①② B.②③④ C.①②④ D.①②③④
二 、填空题
13.已知▱ABCD中一条对角线分∠A为35°和45°,则∠B= .
14.在平行四边形ABCD中,已知AD=10cm,AB垂直于BD,点O是两条对角线的交点,OD=4cm,则AB= cm.
15.在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于 .
16.如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,请添加一个条件 ,使四边形AECF是平行四边形(只填一个即可).
17.已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x= .
18.如图,在▱ABCD中,对角线AC与BD交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折,若点B的落点记为B′,则DB′的长为 .
三 、作图题
19.如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,求CE.
四 、解答题
20.已知▱ABCD中,AC是对角线,BE平分∠ABC交AC于点E,DF平分∠ADC交AC于点F.
求证:AE=CF.
21.如图,在▱ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
(1)若∠F=40°,求∠A的度数;
(2)若AB=10,BC=16,CE⊥AD,求▱ABCD的面积.
22.如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.
23.如图,已知▱ABCD中,DM⊥AC于M,BN⊥AC于N.
求证:四边形DMBN为平行四边形.
24.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
25.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
答案
1.B;
2.B.
3.C.
4.D
5.C.
6.B
7.B.
8.A
9.A.
10.C.
11.C.
12.C
13.答案为:100°.
14.答案为:6.
15.答案为:2.
16.答案为:AF=CE.
17.答案为:4或﹣2.
18.答案为:.
19.解:(1)如答图所示,E点即为所求;
(2)∵四边形ABCD是平行四边形,
∴AB=CD=5,AD∥BC,
∴∠DAE=∠AEB,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴BE=BA=5,
∴CE=BC-BE=3.
20.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠ABC=∠CDA,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CDF,
∵AB∥CD,
∴∠BAE=∠DCF
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF.
21.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=40°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=40°,
∴∠A=180°﹣40°﹣40°=100°
(2)∵∠AEB=∠ABE
∴AE=AB=10
∵四边形ABCD是平行四边形
∴AD=BC=16,CD=AB=10,
∴DE=AD﹣AE=6,
∵CE⊥AD,
∴CE=8,
∴▱ABCD的面积=AD•CE=16×8=128
22.解:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
∴EB=CF
23.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAM=∠BCN,
∵DM⊥AC,BN⊥AC,
∴DM∥BN,∠AMD=∠CNB=90°,
在△ADM和△CBN中,
,
∴△ADM≌△CBN(AAS),
∴DM=BN,
∴四边形DMBN为平行四边形.
24.证明:(1)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,即:∠EAB=∠DAC,
∴△ABE≌△ACD(SAS);
(2)证明:∵△ABE≌△ACD,
∴BE=DC,∠EBA=∠DCA,
又∵BF=DC,
∴BE=BF.
∵△ABC是等边三角形,
∴∠DCA=60°,
∴△BEF为等边三角形.
∴∠EFB=60°,EF=BF
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABC=∠EFB,
∴EF∥BC,即EF∥DC,
∵EF=BF,BF=DC,
∴EF=DC,
∴四边形EFCD是平行四边形.
25.证明:(1)作AM⊥BC于M,如图所示:
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,
∴AB=AC,
∴BM=CM,
∴AM=BC=5,
∵AD∥BC,
∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,
∴5﹣t=2t﹣2,解得:t=,
BQ=BC﹣CQ=10﹣2×= ;
(2)存在,t=4;理由如下:若以A,B,E,P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10﹣2t+2,解得:t=4,
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4.









