北师大版数学七年级下册 4.1.1 三角形的概念及内角和定理 课件

这是一份北师大版数学七年级下册 4.1.1 三角形的概念及内角和定理 课件，共27页。

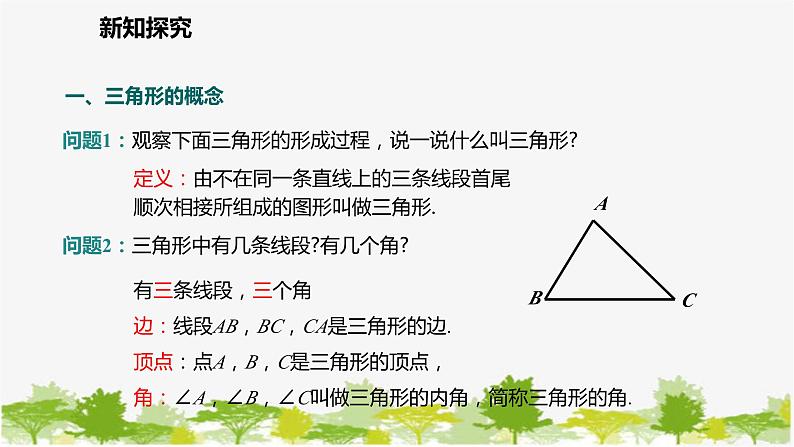
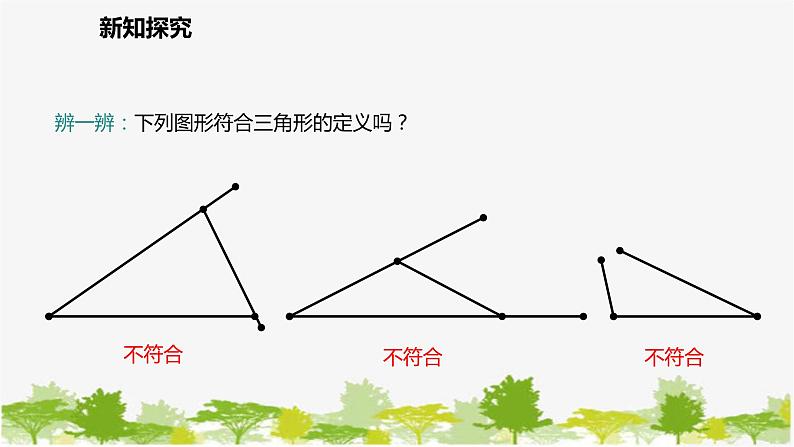
第四章三角形4.1.1 三角形的概念及内角和定理七年级数学北师版·下册教学目标1.认识三角形并会用几何语言表示三角形，了解三角形分类.3.会运用三角形内角和定理进行计算.（难点）2.会用平行线的性质与平角的定义证明三角形内角和等于180°.（重点）新课导入建筑物高楼大厦新知探究飞机机翼水分子结构示意图新知探究问题：（1）从高楼大厦到飞机，从宏伟的建筑物到微小的分子结构，都有什么样的形状？（2）在我们的生活中有没有这样的形状呢？试举例.新知探究问题1：观察下面三角形的形成过程，说一说什么叫三角形?定义：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.A B C 问题2：三角形中有几条线段?有几个角?有三条线段，三个角边：线段AB，BC，CA是三角形的边.顶点：点A，B，C是三角形的顶点，角：∠A，∠B，∠C叫做三角形的内角，简称三角形的角.一、三角形的概念新知探究记法：三角形ABC用符号表示________.边的表示：三角形ABC的边AB，AC和BC可用小写字母分别表示为________.△ABCc，b，a边c边b边a顶点C角角角顶点A顶点B新知探究辨一辨：下列图形符合三角形的定义吗？不符合不符合不符合新知探究①位置关系：不在同一直线上；②连接方式：首尾顺次.三角形应满足以下两个条件：要点提醒表示方法：三角形用符号“△”表示；记作“△ABC”，读作“三角形ABC”，除此△ABC还可记作△BCA，△ CAB，△ ACB等.新知探究三角形的三个内角拼到一起恰好构成一个平角.观测的结果不一定可靠，还需要通过数学知识来说明.从上面的操作过程，你能发现证明的思路吗？还有其他的拼接方法吗？探究：在纸上任意画一个三角形，将它的内角剪下拼合在一起.二、三角形的内角和新知探究验证结论三角形三个内角的和等于180°.求证：∠A+∠B+∠C=180°.已知：△ABC.证法1：过点A作l∥BC，所以∠B=∠1 (两直线平行,内错角相等) ，所以∠C=∠2(两直线平行，内错角相等) .因为∠2+∠1+∠BAC=180°，所以∠B+∠C+∠BAC=180°.12新知探究证法2：延长BC到D，过点C作CE∥BA，所以 ∠A=∠1(两直线平行，内错角相等)，所以∠B=∠2(两直线平行，同位角相等).又因为∠1+∠2+∠ACB=180°，所以∠A+∠B+∠ACB=180°.ED新知探究EDF证法3：过点D作DE∥AC，作DF∥AB，所以∠C=∠EDB，∠B=∠FDC(两直线平行，同位角相等)，所以∠A+∠AED=180°，所以∠AED+∠EDF=180°(两直线平行，同旁内角互补)，所以 ∠A=∠EDF. 因为∠EDB+∠EDF+∠FDC=180°，所以∠A+∠B+∠C=180°.新知探究思考：多种方法证明三角形内角和等于180°的核心是什么？借助平行线的“移角”的功能，将三个角转化成一个平角.12新知探究知识要点在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线.在平面几何里，辅助线通常画成虚线.思路总结为了证明三个角的和为180°，转化为一个平角或同旁内角互补等，这种转化思想是数学中的常用方法.作辅助线新知探究练习：1. 求出下列各图中的x值．x=70 x=60x=30 x=50 新知探究练习：2. 在△ABC 中， ∠A 的度数是∠B 的度数的3倍，∠C 比∠B 大15°，求∠A，∠B，∠C的度数.解: 设∠B为x°，则∠A为(3x)°，∠C为(x ＋ 15)°， 从而有3x ＋ x ＋(x ＋ 15)＝ 180，解得 x ＝ 33，所以 3x ＝ 99 ， x ＋ 15 ＝ 48，答： ∠A， ∠B， ∠C的度数分别为99°， 33°， 48°.几何问题借助方程来解， 这是一个重要的数学思想.新知探究问题1：观察下列三角形，说一说，按照三角形内角的大小，三角形可以分为哪几类？直角三角形 锐角三角形 钝角三角形三、三角形的分类新知探究问题2：如图所示是我们常用的三角板，两锐角的度数之和为多少度?问题引导新知探究问题3：如图，在Rt△ABC中， ∠C=90°，两锐角的和等于多少呢？思考：由此，你可以得到直角三角形有什么性质呢？新知探究直角三角形的两个锐角互余．　　应用格式：在Rt△ABC 中，因为∠C =90°，所以∠A +∠B =90°．　直角三角形的表示：直角三角形可以用符号“Rt△”表示，直角三角形ABC 可以写成Rt△ABC ．总结归纳新知探究方法一（利用平行的判定和性质）：因为∠B=∠C=90°，所以AB∥CD，所以∠A=∠D.方法二（利用直角三角形的性质）：因为∠B=∠C=90°，所以∠A+∠AOB=90°，∠D+∠COD=90°.因为∠AOB=∠COD，所以∠A=∠D.例 如图，∠B=∠C=90°，AD交BC于点O，∠A与∠D有什么关系？典例精析┐┐O课堂小结由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.三角形的概念：三角形三个内角的和等于180°.三角形内角和定理：三角形的分类：按照三角形内角的大小，三角形可以分为直角三角形、锐角三角形和钝角三角形.直角三角形的两个锐角互余．　　直角三角形的性质：课堂小测1.如图所示，△ABC为直角三角形，∠ACB=90°，CD⊥AB，与∠1互余的角有（　　）A．∠B B．∠A C．∠BCD和∠A D．∠BCD C课堂小测（2）在△ABC中，∠A :∠B:∠C=1:2:3，则△ABC是_________三角形 ； 2. 填空：（1）在△ABC中，∠A=35°，∠ B=43 °，则∠ C= ； （3）在△ABC中， ∠A= ∠B+10°, ∠C= ∠A + 10°, 则∠A= ， ∠ B= ，∠ C= .102°直角60°50°70°课堂小测3. 如图，一张长方形纸片，剪去一部分后得到一个三角形，则图中∠1+∠2的度数是________.90°4.如图，AB，CD相交于点O，AC⊥CD于点C，若∠BOD=38°，则∠A=___.52°第3题图第4题图课堂小测5. 如图，四边形ABCD中，点E在BC上，∠A+∠ADE=180°，∠B=78°，∠C=60°，求∠EDC的度数．解：因为∠A+∠ADE=180°， 所以AB∥DE， 所以∠CED=∠B=78°． 又因为∠C=60°， 所以∠EDC=180°-（∠CED+∠C） =180°-（78°+60°） =42°．