初中2.4 线段、角的轴对称性教课内容ppt课件

这是一份初中2.4 线段、角的轴对称性教课内容ppt课件，共16页。PPT课件主要包含了几何语言，已知线段AB，∵CACB，∵DADB，简写成，线段两端等内容，欢迎下载使用。

1.线段是轴对称图形吗？
线段是轴对称图形，有两条对称轴线段的垂直平分线和它本身所在的直线是它的对称轴.
线段的垂直平分线上的点到线段的两个端点的距离相等.
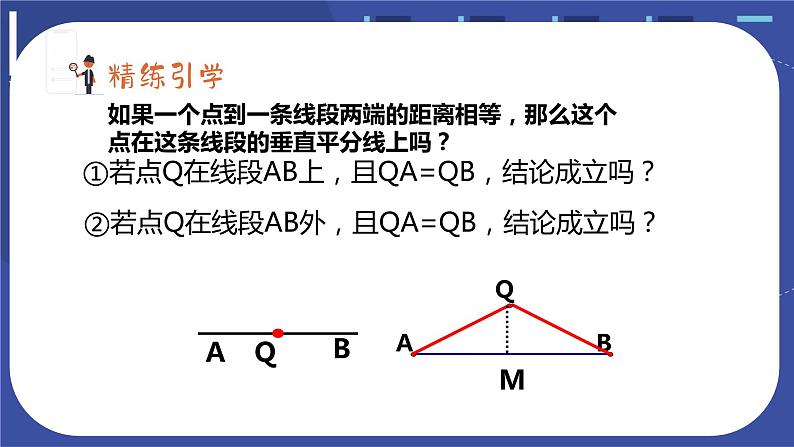
①若点Q在线段AB上，且QA=QB，结论成立吗？
②若点Q在线段AB外，且QA=QB，结论成立吗？
如果一个点到一条线段两端的距离相等，那么这个点在这条线段的垂直平分线上吗？
情况一 ：点P在线段上
情况二 :点P在线段外
（1）当点P在线段AB上时，∵PA=PB，∴点P为线段AB的中点，显然此时点P在线段AB的垂直平分线上.
已知：如图，PA＝PB，求证：点P在线段AB的垂直平分线上.
证明：过点P 作AB 的垂线PC，垂足为点C．则∠PCA =∠PCB =90°．在Rt△PCA 和Rt△PCB 中， PA =PB，PC =PC，∴ Rt△PCA ≌Rt△PCB（HL）．∴ AC =BC．又 PC⊥AB，∴ 点P 在线段AB 的垂直平分线上．
这些点能组成什么几何图形？
你能再找一些到线段AB 两端点的距离相等的点吗？能找到多少个到线段AB 两端点距离相等的点？
直线l 可以看成与两点A、B 的距离相等的所有点的集合．
线段垂直平分线是到线段两端距离相等的点的集合．
用尺规作线段垂直平分线
求作：AB的垂直平分线.
∴点C在线段AB的垂直平分线上
∴点D在线段AB的垂直平分线上
∴CD是线段AB的垂直平分线
∵CA=CB，DA=DB
证明：连接CA、CB、DA、DB
例1 已知：如图，在△ABC中，AB ，AC的垂直平分线l1，l2相交于点O．求证：点O在BC的垂直平分线上．
证明：连接OA，OB ， OC.∵ AB ， AC的垂直平分线l1，l2相交于点O ，∴OA=OB ， OA＝OC ，∴OB=OC ，∴点O在BC的垂直平分线上．
1.如图，AB=AC，DB=DC，E是AD延长线上的一点，BE是否与CE相等？试说明理由.
解：相等. 连接BC，∵AB=AC，∴点A在线段BC的垂直平分线上.同理，D点也在线段BC的垂直平分线上.∵两点确定一条直线，∴AD是线段BC的垂直平分线，∵E是AD延长线上的一点，∴BE=CE.
2.如图，在△ABC中，分别以点A和点B为圆心，大于 AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为_____．
1.如图，在△ABC中，点D在BC上，且BC=BD+AD，则点D在_____的垂直平分线上．
3.如图所示，AC=AD，BC=BD，则下列说法正确的是（　 ） A．AB垂直平分CD； B ．CD垂直平分AB ； C．AB与CD互相垂直平分； D．CD平分∠ ACB ．
4.如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的关系．
解：AD垂直平分EF.∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴∠EAD＝∠FAD，∠AED＝∠AFD=90°.又∵AD＝AD，∴△ADE≌△ADF，∴AE＝AF，DE＝DF.∴直线AD垂直平分线段EF.
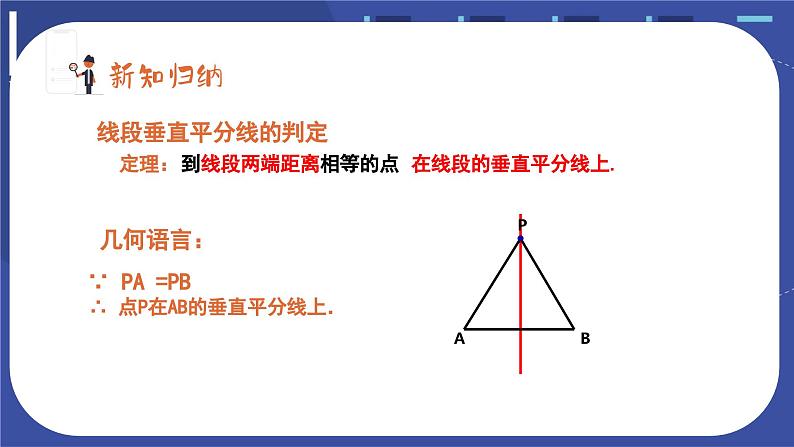
知识点一　线段垂直平分线的判定
到　　　　　　距离相等的点在线段的垂直平分线上. 
知识点二　尺规作图——作线段的垂直平分线
如图,作线段AB的垂直平分线,分别以点　　　　为圆心,以　　　　　　　　为半径画两条弧,两弧相交于两个点,过这两个交点的直线就是线段AB的垂直平分线.