人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定说课ppt课件

这是一份人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定说课ppt课件，共18页。PPT课件主要包含了观察思考，三角形中有三条中位线，你能证明以上猜想吗，方法二，方法三，方法四，知识拓展，课堂小结，两层含义如图等内容，欢迎下载使用。
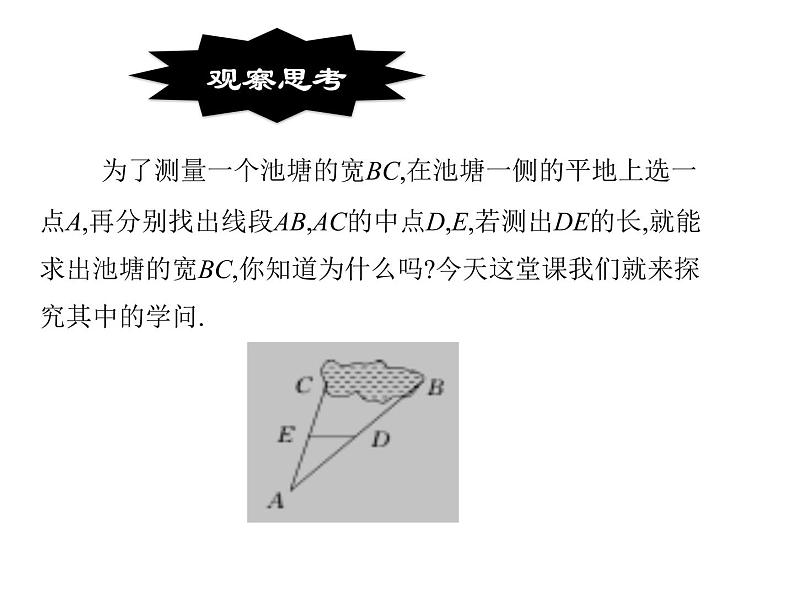
　 为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D,E,若测出DE的长,就能求出池塘的宽BC,你知道为什么吗?今天这堂课我们就来探究其中的学问.
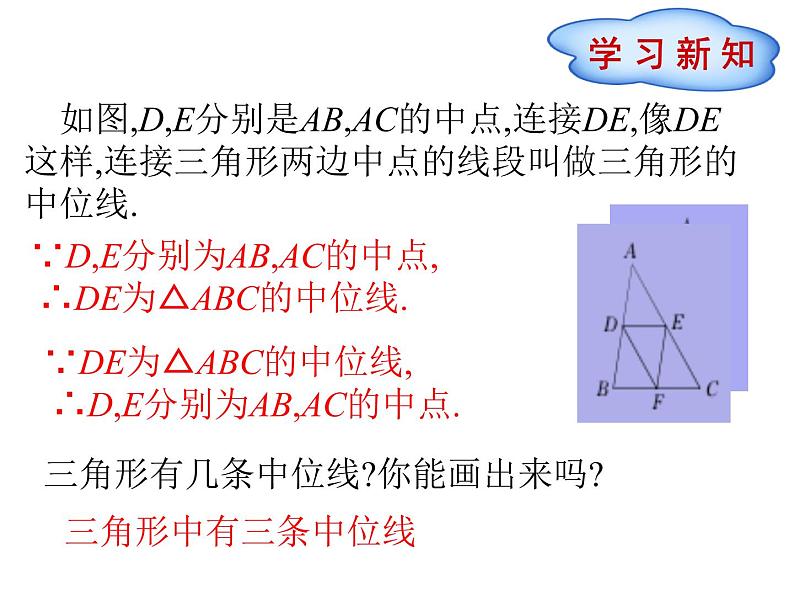
　如图,D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
∵D,E分别为AB,AC的中点, ∴DE为△ABC的中位线.
三角形有几条中位线?你能画出来吗?
∵DE为△ABC的中位线, ∴D,E分别为AB,AC的中点.
　　说出三角形的中位线与中线有何相同点和不同点.
相同之处:都是和边的中点有关的线段.
不同之处:三角形中位线的两个端点都是边的中 点;三角形中线只有一个端点是边的中 点,另一端点是三角形的顶点.
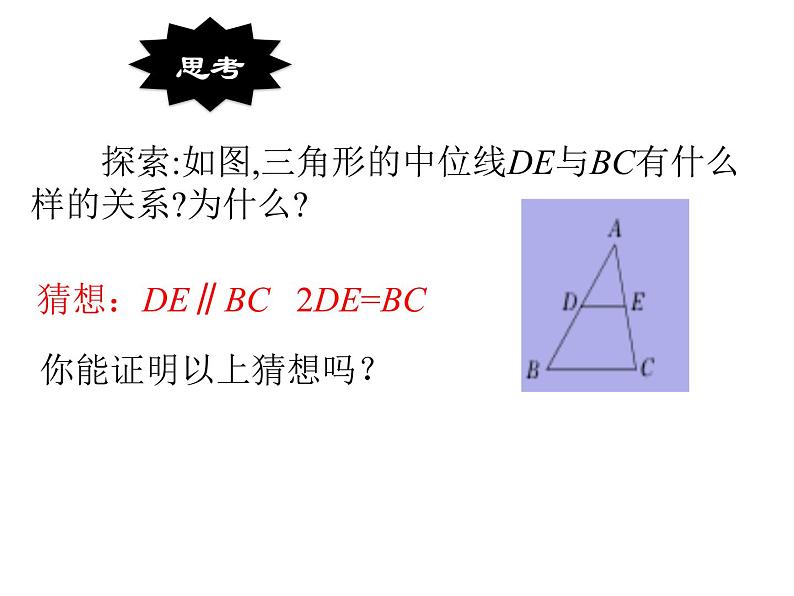
　　探索:如图,三角形的中位线DE与BC有什么样的关系?为什么?
猜想：DE∥BC 2DE=BC
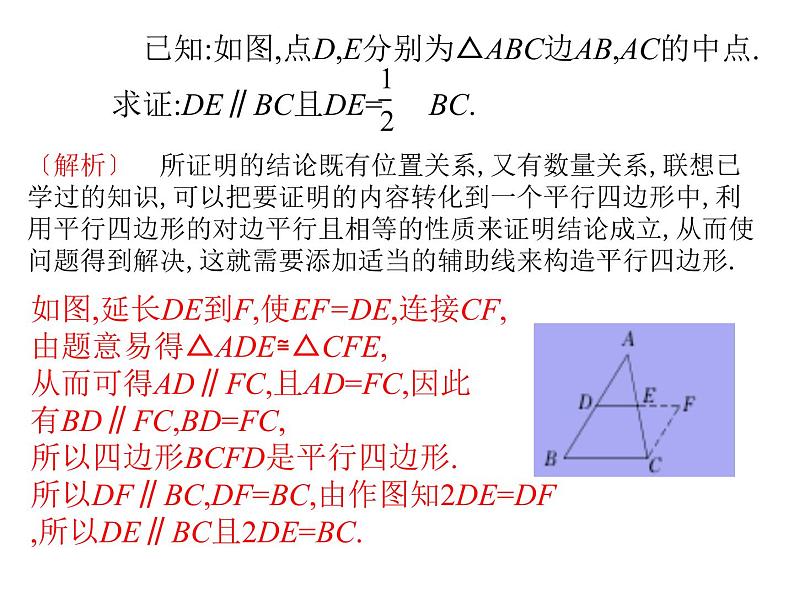
　已知:如图,点D,E分别为△ABC边AB,AC的中点.求证:DE∥BC且DE= BC.　
〔解析〕　所证明的结论既有位置关系,又有数量关系,联想已学过的知识,可以把要证明的内容转化到一个平行四边形中,利用平行四边形的对边平行且相等的性质来证明结论成立,从而使问题得到解决,这就需要添加适当的辅助线来构造平行四边形.
如图,延长DE到F,使EF=DE,连接CF,由题意易得△ADE≌△CFE,从而可得AD∥FC,且AD=FC,因此有BD∥FC,BD=FC,所以四边形BCFD是平行四边形.所以DF∥BC,DF=BC,由作图知2DE=DF,所以DE∥BC且2DE=BC.
如图,延长DE到F,使EF=DE,连接CF,CD和AF,因为AE=EC,所以四边形ADCF是平行四边形.所以AD∥FC,且AD=FC.因为AD=BD,所以BD∥FC,且BD=FC.所以四边形BCFD是平行四边形.所以DF∥BC,且DF=BC,因为2DE=DF,所以DE∥BC且2DE=BC.
如图,过E点作AB的平行线交BC于N,交过A点与BC平行的直线于M,由题意及作图易知△AEM≌△CEN,可得ME=EN,AM=CN,因为AM∥BC,AB∥MN,所以四边形AMNB是平行四边形,所以AB=MN,AM=BN.又因为2BD=AB,2EN=MN,所以BD=EN,所以四边形BDEN是平行四边形,则DE=BN,DE∥BC,所以DE=BN=AM=CN,即2DE=BC.
如图,过A,B,C三点分别作DE的垂线,分别交直线DE于点P,M,N.因为AP,BM,CN都垂直于DE,所以AP∥BM∥CN.可证明△APE≌△CNE,则AP=CN,PE=EN,△ADP≌△BDM，则AP=BM,MD=DP,所以BM=CN,2DE=MN,所以四边形BMNC是平行四边形,所以DE∥BC,2DE=MN=BC.
三角形中位线的性质:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
∵D,E分别是AB,AC的中点,　∴DE∥BC,DE= BC.
(1)三角形的中位线所构成的三角形的周长是 原三角形周长的一半.
(2)三角形三条中位线可以把三角形分成三个 平行四边形,分成的四个三角形全等.
(3)三角形三条中位线所构成的三角形的面积 等于原三角形面积的四分之一.
　 例： 如图,△ABC的中位线DE=5 cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A,F两点间的距离是8 cm,求△ABC的面积.
　解:连接AF,如图所示.∵DE是△ABC的中位线,　∴BC=2DE=10 cm,DE∥BC.　由折叠可知AF⊥DE,∴AF⊥BC,　∴AF是△ABC的边BC上的高.　∵AF=8 cm,　∴S△ABC= BC·AF= ×10×8=40(cm2).
　 [归纳拓展]　本题还可以这样解:△ABC的面积是四边形ADFE面积的2倍,而四边形ADFE的对角线互相垂直,因此它的面积等于对角线乘积的一半,所以△ABC的面积等于AF·DE.
　 例： 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证四边形EFGH是平行四边形.
　〔解析〕因为已知点E,F,G,H分别是线段的中点,所以可以设法应用三角形中位线性质找到四边形EFGH的边之间的关系.由于四边形的一条对角线可以把四边形分成两个三角形,所以考虑添加辅助线,连接AC或BD,构造含有三角形中位线的基本图形后,此题便可得证.
　证明:连接AC,如图所示.　在△DAC中,∵AH=HD,CG=GD,　∴HG∥AC,HG= AC(三角形中位线性质).　同理可得EF∥AC,EF= AC. ∴HG∥EF,且HG=EF.　∴四边形EFGH是平行四边形.
[归纳总结]顺次连接四边形四条边的中点,所得的四边 形是平行四边形.
三角形的中位线的定义:连接三角形两边中点的线段叫做三角形的中位线.
①∵D,E分别为AB,AC的中点, ∴DE为△ABC的中位线;
②∵DE为△ABC的中位线, ∴D,E分别为AB,AC的中点.　
三角形中位线的性质:　 三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
特点:在一个题设下,有两个结论.一个表示位置关系,另一个表示数量关系.
结论:有两个,一个表明中位线与第三边的位置关系,另一个表明中位线与第三边的数量关系.
三角形中位线的性质:三角形的中位线平行于第三边并且等于第三边的一半.∵D,E分别是AB,AC的中点,∴DE∥BC, DE=BC.
作用:在已知两边中点的条件下,证明线段的平行关系及线段的倍分关系.
1.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20 m,那么A,B两点间的距离是　　m,理由是 　 .
解析:因为M,N分别是AC和BC的中点,所以2MN=AB,所以AB=2MN=40 m.理由是:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
三角形的中位线平行于三角形的第三边,并且等于第三边的一半
2.Rt△ABC中,∠C=90°,AB=10,AC=8,BC=6,点D,E,F分别是△ABC三边的中点,则△DEF的周长是　　　　,面积是　　　　. 
解析:△DEF的三条边分别是Rt△ABC的三条中位线,所以△DEF的三条边长分别是Rt△ABC的三边长的一半,所以△DEF的周长是Rt△ABC的周长的一半,△ABC的周长是24,则△DEF的周长是12.三角形的三条中位线在三角形中可以构成三个平行四边形和四个全等的三角形,所以△DEF的面积是Rt△ABC的面积的四分之一,△ABC的面积= 8× 6=24,因此△DEF的面积为6.