北师大版数学八年级下册 1.3.2 《线段的垂直平分线（2）》课件+分层练习（含答案解析）

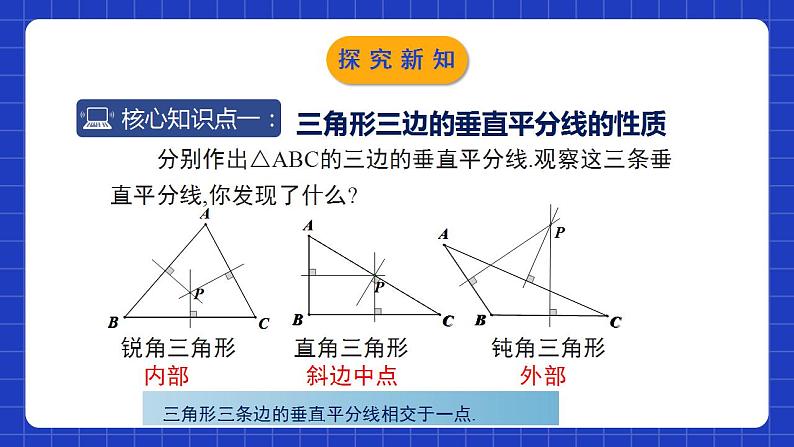
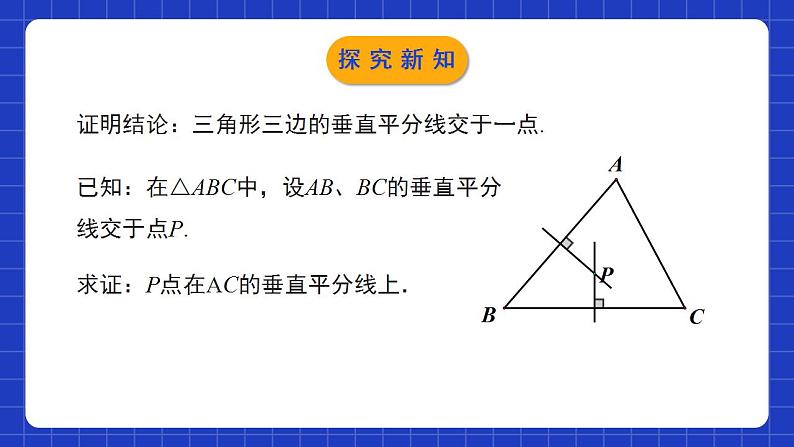
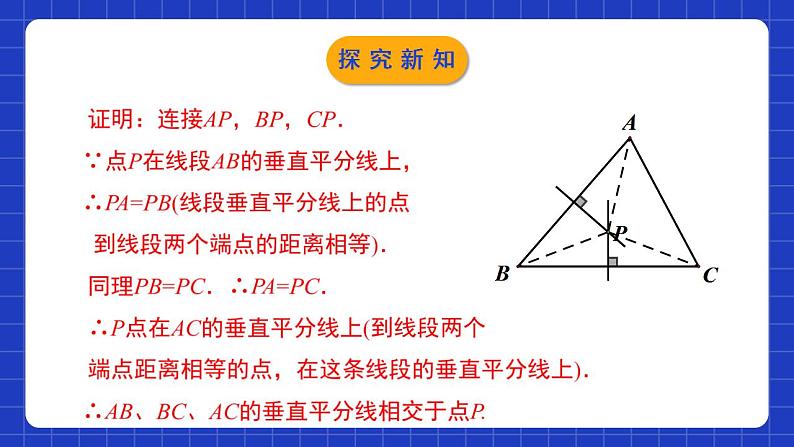
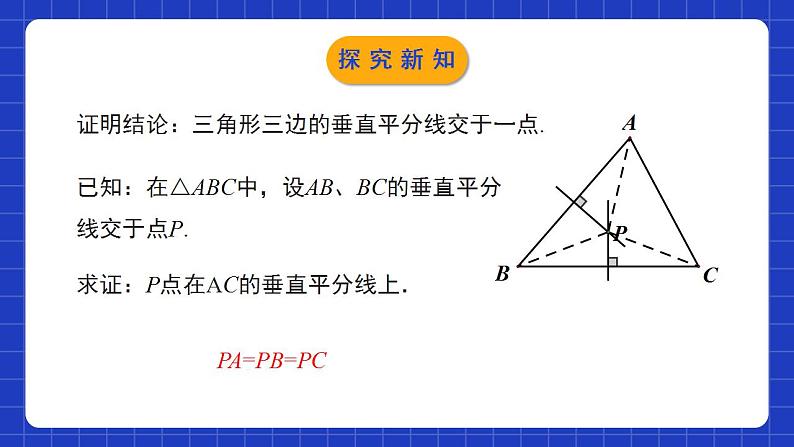
1.3.2线段的垂直平分线（2）学习目标理解并掌握三角形三边的垂直平分线的性质.0102能够运用三角形三边的垂直平分线的性质解决实际问题.能够利用尺规作已知底边及底边上的高的等腰三角形.031.线段的垂直平分线的性质定理线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段的垂直平分线的判定定理到一条线段两个端点距离相等的点，在这条线段的垂直平分线上.情境导入 某区政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问该购物中心应建于何处，才能使得它到三个小区的距离相等？猜想：三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等。情境导入三角形三边的垂直平分线的性质 分别作出△ABC的三边的垂直平分线.观察这三条垂直平分线,你发现了什么?锐角三角形直角三角形钝角三角形 三角形三条边的垂直平分线相交于一点.内部斜边中点外部探究新知证明结论：三角形三边的垂直平分线交于一点.已知：在△ABC中，设AB、BC的垂直平分线交于点P.求证：P点在AC的垂直平分线上．探究新知 证明：连接AP，BP，CP． ∵点P在线段AB的垂直平分线上， ∴PA=PB(线段垂直平分线上的点 到线段两个端点的距离相等)． 同理PB=PC．∴PA=PC． ∴P点在AC的垂直平分线上(到线段两个 端点距离相等的点，在这条线段的垂直平分线上)． ∴AB、BC、AC的垂直平分线相交于点P.探究新知证明结论：三角形三边的垂直平分线交于一点.已知：在△ABC中，设AB、BC的垂直平分线交于点P.求证：P点在AC的垂直平分线上．PA=PB=PC探究新知证明：∵ 点 P 在线段 AB 的垂直平分线上，∴ PA=PB（线段垂直平分线上的点到这条线段两个端点的距离相等）.同理，PB=PC. ∴ PA=PB=PC.求证： 三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.探究新知归纳总结定理：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.几何语言：在△ABC中，∵a，b，c分别是BC，AC，AB的垂直平分线，∴a，b，c相交于点P，且PA=PB=PC.点P称为三角形的外心探究新知例.在联欢晚会上，三名同学站在一个非等边三角形的三个顶点A，B，C位置上，他们在玩抢凳子游戏，要求在他们中间放一个凳子，谁先抢到凳子谁获胜，为使游戏公平，凳子(用点P表示)应放在哪个位置？请用尺规作图找出点P.探究新知尺规作图思考：(1)已知三角形的一条边及这条边上的高， 你能作出三角形吗？如果能，能作几个？所作出的三角形都全等吗？能作出无数个，所作出的三角形不全等探究新知 (2) 已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗?能作几个?能作出2个。在底边的两侧所作出的三角形全等。hh探究新知例：已知一个等腰三角形的底边及底边上的高， 求作这个等腰三角形.已知：如图，线段a，h.求作： △ABC，使AB=AC，且BC=a，高AD= h. 作法：（1）作线段BC=a.（2）作线段BC的垂直平分线l，交BC于点D.（3）在l上作线段DA，使DA= h.（4）连接AB，AC. △ABC为所求作的等腰三角形.ahABCD 注意：点A关于BC的对称点A′也符合题意.探究新知已知直线l和l上一点P，利用尺规作l的垂线，使它经过点P .如果点P在直线l外呢？mm探究新知1.三角形三边的垂直平分线的交点(　　)A.到三角形三边的距离相等B.到三角形三个顶点的距离相等C.到三角形三个顶点与三条边的距离相等D.不能确定B随堂练习2. 如图，D是线段AC，AB的垂直平分线的交点，若∠ACD＝30°，∠BAD＝50°，则∠BCD的大小是(　　)A．10° B．20° C．30° D．40°A随堂练习3.如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC.△ABC为所求作的等腰三角形.上述作法的四个步骤中,你认为有错误的一步是(　　)A.(1) B.(2) C.(3) D.(4) C随堂练习4.如图，O为△ABC三边垂直平分线的交点，若∠OAB＝30°，∠OBC＝20°，则∠OCA＝________.40°5. 如图,O为△ABC三边垂直平分线的交点,点O到顶点A的距离为5 cm,则AO+BO+CO=　　cm. 15随堂练习6.如图，在△ABC中，∠A＞∠B.(1)作边AB的垂直平分线DE，与AB、BC分别相交于点D、E(用尺规作图，保留作图痕迹，不要求写作法)；(2)在(1)的条件下，连接AE，若∠B＝50°，求∠AEC的度数.(2)∵DE垂直平分AB，∴AE＝BE∴∠EAB＝∠B＝50°∵∠AEC是△ABE的外角∴∠AEC＝∠EAB＋∠B＝100°随堂练习7.如图，一机器人在点A处发现一个小球自点B处沿x轴向原点O方向匀速滚去，机器人立即从A处匀速直线前进，去截小球，若小球滚动速度与机器人行走速度相等．试在图中标出机器人恰好能截住小球的位置C.(保留作图痕迹)随堂练习8.如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＝3，AC的垂直平分线DE分别交AB，AC于D，E两点，求CD的长.随堂练习9.如图，已知△ABE中，AB，AE边的垂直平分线m1，m2分别交BE于点C，D，且BC＝CD＝DE.(1)求证：△ACD是等边三角形；(2)求∠BAE的度数.(1)证明：∵C，D分别是线段AB，AE垂直平分线m1，m2上两点∴AC＝BC，AD＝ED∵BC＝CD＝DE，∴AC＝AD＝CD∴△ACD是等边三角形随堂练习9.如图，已知△ABE中，AB，AE边的垂直平分线m1，m2分别交BE于点C，D，且BC＝CD＝DE.(1)求证：△ACD是等边三角形；(2)求∠BAE的度数.(2)解：∵AC＝BC，AD＝ED∴∠BAC＝∠B，∠EAD＝∠E∵∠ACD＝∠ADC＝60°∴∠BAC＋∠B＝∠EAD＋∠E＝60°∴∠BAC＝∠EAD＝30°∴∠BAE＝30°＋60°＋30°＝120°随堂练习线段的垂直平分线三角形三边的垂直平分线的性质尺规作图三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等课堂小结课程结束